Description
小Y最近在一家金券交易所工作。该金券交易所只发行交易两种金券:A纪念券(以下简称A券)和 B纪念券(以下
简称B券)。每个持有金券的顾客都有一个自己的帐户。金券的数目可以是一个实数。每天随着市场的起伏波动,
两种金券都有自己当时的价值,即每一单位金券当天可以兑换的人民币数目。我们记录第 K 天中 A券 和 B券 的
价值分别为 AK 和 BK(元/单位金券)。为了方便顾客,金券交易所提供了一种非常方便的交易方式:比例交易法
。比例交易法分为两个方面:(a)卖出金券:顾客提供一个 [0,100] 内的实数 OP 作为卖出比例,其意义为:将
OP% 的 A券和 OP% 的 B券 以当时的价值兑换为人民币;(b)买入金券:顾客支付 IP 元人民币,交易所将会兑
换给用户总价值为 IP 的金券,并且,满足提供给顾客的A券和B券的比例在第 K 天恰好为 RateK;例如,假定接
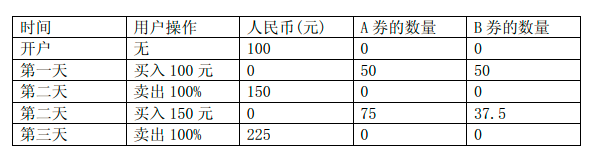
下来 3 天内的 Ak、Bk、RateK 的变化分别为:

假定在第一天时,用户手中有 100元 人民币但是没有任何金券。用户可以执行以下的操作:

注意到,同一天内可以进行多次操作。小Y是一个很有经济头脑的员工,通过较长时间的运作和行情测算,他已经
知道了未来N天内的A券和B券的价值以及Rate。他还希望能够计算出来,如果开始时拥有S元钱,那么N天后最多能
够获得多少元钱。
Input
输入第一行两个正整数N、S,分别表示小Y能预知的天数以及初始时拥有的钱数。接下来N行,第K行三个实数AK、B
K、RateK,意义如题目中所述。对于100%的测试数据,满足:0<AK≤10;0<BK≤10;0<RateK≤100;MaxProfit≤1
0^9。
【提示】
1.输入文件可能很大,请采用快速的读入方式。
2.必然存在一种最优的买卖方案满足:
每次买进操作使用完所有的人民币;
每次卖出操作卖出所有的金券。
Output
只有一个实数MaxProfit,表示第N天的操作结束时能够获得的最大的金钱数目。答案保留3位小数。
Sample Input
3 100
1 1 1
1 2 2
2 2 3
1 1 1
1 2 2
2 2 3
Sample Output
225.000
HINT
题解
可以发现每次买入和卖出一定是使用全部的资产。
那么,令$f_i$表示第i天开始时最大可持有多少现金(金券不算),$x_i=frac{f_i}{Rate_iA_i+B_i}$表示这些现金换成金券时有多少$B$券,$y_i=Rate_ix_i$表示有多少A券,那么有
$$f_i = maxleft(f_{i-1}, max{y_jA_i+x_jB_imid j < i} ight)$$
熟悉双变量线性规划的可以看出来把$x,y$画到平面上,用一个斜率为$-frac{B_i}{A_i}$的直线经过这些点,选出最靠上的,这个点便是最优点。
那么可以看出,最优解一定在前面所有点的上凸壳上。
但是点的横纵坐标都不是单调的,怎么办呢?
1.利用平衡树维护凸包。
2.CDQ分治。
我们发现,只有编号小的会对编号大的产生影响,那么我们按时间把所有天分成两半,先递归解决前一半,然后将前一半按横坐标排序,求凸包,后一半按$-frac{B_i}{A_i}$排序,更新后一半的答案后再递归解决后一半即可。
实现中,按横坐标排序需要归并排序,按斜率排序只需要开头排一遍即可。
时间复杂度是常见的$T(n)=2T(frac n 2) + O(n)$,$T(n) = O(nlogn)$。
附代码(其实代码里的注释是给我自己写的,毕竟第一次写CDQ):
#include <algorithm>
#include <cstdio>
#include <cmath>
using std::abs;
const int N = 100050;
const double eps = 1e-6;
struct Info{
double a, b, rate;
double k, x, y;
int i;
bool operator<(const Info &t)const{
return k > t.k;
}
};
double f[N];
Info p[N], tmp[N];
Info cv[N];
inline bool cmp(const Info &a, const Info &b) {
if (fabs(a.x - b.x) < eps) return a.y > b.y;
return a.x < b.x;
}
inline double getK(const Info &a, const Info &b) {
return (a.y - b.y) / (a.x - b.x);
}
inline double calc(const Info &a, const Info &b) {
return a.x * b.b+ a.y * b.a;
}
void solve(int l, int r) { //[l, r)
if (r - l <= 1) {
if (l) f[l] = std::max(f[l], f[l - 1]);
p[l].x = f[l] / (p[l].rate * p[l].a + p[l].b);
p[l].y = p[l].x * p[l].rate;
return;
}
int mid = (l + r) >> 1;
int p1 = l, p2 = mid;
//split [l, r) to [l, mid) and [mid, r)
for (int i = l; i < r; ++i) {
if (p[i].i < mid) tmp[p1++] = p[i];
else tmp[p2++] = p[i];
}
for (int i = l; i < r; ++i)
p[i] = tmp[i];
//solve the left half
solve(l, mid);
//get the upper convex hull
int q = 0;
for (int i = l; i < mid; ++i) if (!i || fabs(p[i].x - p[i - 1].x) >= eps) {
while (q > 1 && getK(p[i], cv[q - 1]) > getK(cv[q - 1], cv[q - 2]))
--q;
cv[q++] = p[i];
}
//update the answers of the right half
for (int i = mid, j = 0; i < r; ++i) {
while (j < q - 1 && calc(cv[j + 1], p[i]) > calc(cv[j], p[i]))
++j;
f[p[i].i] = std::max(f[p[i].i], calc(cv[j], p[i]));
}
//solve the right half
solve(mid, r);
//sort the p according to x
int i = l, j = mid, e = l;
while (i < mid && j < r)
if (cmp(p[i], p[j]))
tmp[e++] = p[i++];
else
tmp[e++] = p[j++];
while (i < mid)
tmp[e++] = p[i++];
while (j < r)
tmp[e++] = p[j++];
for (int i = l; i < r; ++i)
p[i] = tmp[i];
}
int main() {
int n;
scanf("%d%lf", &n, &f[0]);
for (int i = 0; i < n; ++i) {
scanf("%lf%lf%lf", &p[i].a, &p[i].b, &p[i].rate);
p[i].k = -p[i].b / p[i].a;
p[i].i = i;
}
std::sort(p, p + n);
solve(0, n);
//for (int i = 0; i < n; ++i)
// printf("%.9lf
", f[i]);
printf("%.3lf
", f[n - 1]);
return 0;
}