1 综合评价模型建立步骤
综合评价模式是一种对一个或多个系统进行评价的模型。一般分为如下几个步骤:
- 选取评价指标,指标的选取应该具有独立性和全面性。
- 得到m×n测量矩阵,每一行表示一个带评价系统(共m行),没一列表示一个评价指标(共n列)。
- 对测量矩阵每个指标进行一致化处理。指标一般有极小型,居中型和区间型,一般都转化为极大型。
- 进行无量纲化处理。常用的方法有标准差法、极值差法、功效系数法等。
- 确定评价指标权重向量。是固定权值还是动态权值?动态权值的隶属函数有分段变幂函数、偏大型正态分布函数、S型分布函数等。
- 建立综合评价模型。线性加权还是非线性加权?
- 给出结论。如果是多对象评价模型可以提供一个排序方法,对评价结果进行排序。
经过上述分析,我们可以确定综合评价模型中应该有如下几个基本类:一致化处理类、无量纲化类、动态权值类和综合评价类。最后还应该有一个模型建立类调用上面几个类提供的方法对模型进行建立并得出结果。
2 一致化处理类
我们在选取评价指标时,可能有多种“值类型”。有越大越好的极大型(如GDP);有居中为佳的居中型(如PH值);有越小越好的极小型(如污染程度)还有在某一范围为最佳的区间型(如人口数)。为了将这些“类型”各异的指标采用相同的模型进行描述,我们需要通过映射将它们的“类型”统一,一般都选择极大型。在映射变换的时候通常有两个原则:保持差值不变和保存比例不变。下面分别讨论如何进行一致化处理。
2.1 区间型化极大型
2.1.1保持变换前后差值不变
假设变换前指标x的取值范围为[minX,maxX],中间有一个区间[bestMin,bestMax]为最佳取值区间。令bestFx = max{(bestMin-minX),(maxX-bestMax)},取变换映射f(x)如下就可以将该指标变换为极大型。

下面是一个使用matlab实现区间型化为极大型(E不变)的一个示例:
%% E不变
clear
clc
maxX = 100;
minX = 0.001;
bestMin = 40;
bestMax = 70;
bestFx = max((bestMin-minX),(maxX-bestMax));
t = linspace(minX,maxX,200);
index1 = t<bestMin;
Ft1 = bestFx-(bestMin-t(index1));
index2 = (t>=bestMin)&(t<=bestMax);
Ft2 = bestFx+t(index2)*0;
index3 = t>bestMax;
Ft3 = bestFx-(t(index3)-bestMax);
plot(t,[Ft1,Ft2,Ft3])
xlabel('x')
ylabel('f(x)')
title('区间型化极大型(E不变)')
执行结果如下:
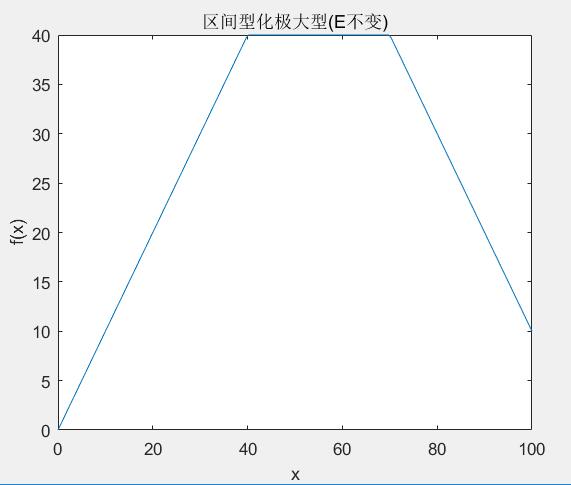
经过上面的映射以后,变换前后的数据差值(绝对值)并不会改变。
2.1.2保持变换前后比例不变
在有的指标数据在变换的时候我们可能更看重数据之间的相对关系。这时候采用变换前后保持同一比例(互为倒数)可能更重要。当然由于和0保持同一比例没有意义,这要求我们的原始数据中不能有0或者非常接近0的数。我们可以采取如下的变换映射进行变换:
下面是使用matlab实现区间型化为极大型(K不变)的一个示例:
clear
clc
maxX = 100;
minX = 0.001;
bestMin = 40;
bestMax = 70;
t = linspace(minX,maxX,200);
index1 = t<bestMin;
Ft1 = t(index1)./bestMin;
index2 = (t>=bestMin)&(t<=bestMax);
Ft2 = 1+t(index2)*0;
index3 = t>bestMax;
Ft3 = bestMax./t(index3);
plot(t,[Ft1,Ft2,Ft3])
执行结果如下:
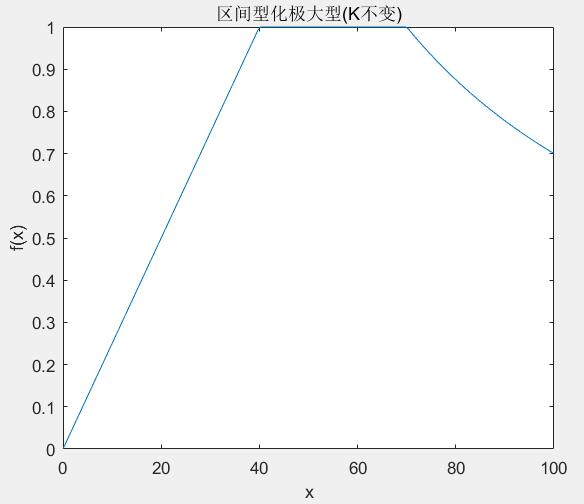
经过上述的映射变换后,我们可以让最优区间内的值映射为1,其他区间的值保持比例不变(或互为倒数)进行映射。
2.2居中型和极小型化为极大型
事实上,居中型是区间型中bestMin=bestMax的一个特例。而极小型是bestMin=bestMax=minX的一个特例。因此我们完全可以使用上面的映射关系进行映射。但是由于它们具有一定的特殊性,我们可以将它们的映射公式进一步简化。
居中型到极大型
- 误差不变
假设最好的x取值为bestX,令bestFx=max{(bestX-minX),(maxX-bestX)}。则:
- 比例不变
映射函数如下:
极小型到极大型
- 误差不变
- 比例不变
2.3C++中一致化处理类
有了上面的分析我们就可以构建C++一致化处理的类了。该类的UML类图描述如下:

该类中提供了极小到极大、居中到极大和范围到极大三个方法。以极小到极大为例,该方法共有4个参数如下:
matrixIn:Matrix
index:Matrix
method:E_Method=ConstError
dir:E_MatrixDir=ColumnDir
第一个参数matrixIn是待处理矩阵,这个参数的类型是Matrix类型(这里我使用的是Eigen矩阵处理库)。
第二个参数index是矩阵中需要处理的列(行)的索引。这个参数的类型是vector
参数method指定处理的方式是保持误差不变还是比例不变。取值为强类枚举类型E_Method,默认保持误差不变。
参数dir表示是按行处理还是按列处理,取值为强枚举类型E_MatrixDir,一般情况下测量矩阵每一行为一个评价系统,每一列为一个评价指标。此时应该是按列处理数据(默认值)。如果矩阵被转置了,则可以手动指定dir=E_MatrixDir::RowDir将矩阵的数据处理方向改为按行处理。
由于这三个方法都是静态方法因此可以直接使用。下面是一致化调用的一个示例:
#include <iostream>
#include <vector>
#include "UnificationMethod.h"
#include "EigenCore"
#include "stdio.h"
using namespace std;
using namespace Eigen;
using namespace CompEvalSpace;
int main()
{
Matrix<double, 3, 3> myMatrix; //被处理矩阵
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
cout << myMatrix << endl<<endl;
vector<int> myVector;
vector<double> vectorMid;
myVector.push_back(1); //处理1,2列
myVector.push_back(2);
cout << "极小型化为极大型:" << endl;
UnificationMethod::MiniTypeToMax<double, 3, 3>(myMatrix, myVector);
cout << myMatrix << endl << endl;
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
vectorMid.push_back(5); //各列的最优居中值
vectorMid.push_back(6);
cout << "居中型化为极大型:" << endl;
UnificationMethod::MidTypeToMax<double, 3, 3>(myMatrix, myVector,vectorMid,E_Method::ConstProportion);
cout << myMatrix << endl<<endl;
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
vector<vector<double> > range(2);
for (vector<vector<double> >::iterator ite = range.begin(); ite != range.end(); ++ite)
{
ite->resize(2);
}
range[0][0] = 5.5; //各列最优区间设置
range[0][1] = 4.5;
range[1][0] = 6.5;
range[1][1] = 5.5;
cout << "区间型化为极大型:" << endl;
UnificationMethod::RangeTypeToMax<double, 3, 3>(myMatrix, myVector, range,E_Method::ConstProportion);
cout << myMatrix << endl << endl;
getchar();
}
执行结果如下:
1 2 3
4 5 6
7 8 9
极小型化为极大型:
1 6 6
4 3 3
7 0 0
居中型化为极大型:
1 0.4 0.5
4 1 1
7 0.625 0.666667
区间型化为极大型:
1 0.444444 0.545455
4 1 1
7 0.6875 0.722222
3 无量纲化处理
不同的指标量纲不同如果在此基础上进行权重的确定,会使权重的确定非常困难。如果能在确定权重之前将量纲的因素减少到最小,那么会使权值的选取更加容易,同时也会让模型的层次性更加清晰。常用的无量纲化处理方法有标准差法、极值差法和功效系数法。关于无量纲化的原理这里不再过多赘述,可以查看综合评价模型的第4章。
除了上面文章中介绍的3中无量纲方法以外,这里又添加了一个归一化的方法。其基本思想和功效系数法相同,但是偏置系数在比例缩放之前就加上了,而且比例系数缩放固定将所有的数据都缩放至0-1之间。即:
3.1无量纲化处理的C++实现
无量纲化类UML模型如下图所示:
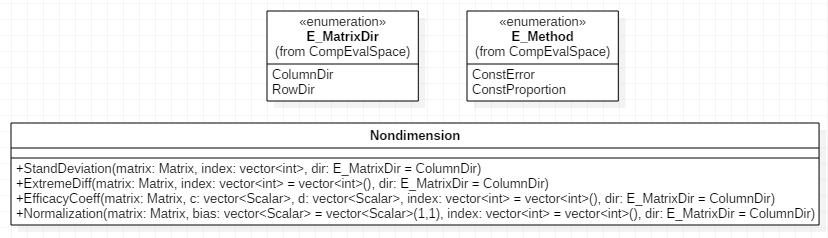
测试代码如下:
cout << "无量纲化" << endl;
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
cout << myMatrix << endl << endl;
cout << "标准差法:" << endl;
Nondimensionalize::StandardDeviation(myMatrix, myVector,E_MatrixDir::RowDir);
cout << myMatrix << endl << endl;
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
cout << "极值差法" << endl;
Nondimensionalize::ExtremeDiff(myMatrix);
cout << myMatrix << endl << endl;
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
cout << "功效系数法" << endl;
vector<double> c, d;
c.push_back(2);
c.push_back(3);
d.push_back(2);
d.push_back(3);
Nondimensionalize::EfficacyCoeff(myMatrix, c, d,myVector);
cout << myMatrix << endl << endl;
myMatrix << 1, 2, 3,
4, 5, 6,
7, 8, 9;
cout << "归一化" << endl;
Nondimensionalize::Normalization(myMatrix);
cout << myMatrix << endl << endl;
执行结果如下:
无量纲化
1 2 3
4 5 6
7 8 9
标准差法:
1 2 3
-1.22474 0 1.22474
-1.22474 0 1.22474
极值差法
0 0 0
0.5 0.5 0.5
1 1 1
功效系数法
1 2 3
4 3 4.5
7 4 6
归一化
0.25 0.333333 0.4
0.625 0.666667 0.7
1 1 1
4 动态加权方法
在数据进行一致化和无量纲化处理以后,接下来就需要确定各个评价指标的权值了。如果我们采用的是固定权值,直接建立一个有m个元素的向量来表示就行。如果我们需要使用动态加权的方法,这里提供了几个动态加权的隶属函数,分别是:分段变幂函数、偏大型正态分布函数和S型分布函数。在使用这些函数之前必须要保证变换后的测量矩阵的数据范围为0-1.
4.1 偏大型分布函数参数的确定
对于偏大型分布函数的两个参数
的确定,我们可以认为
决定了数据的死区大小,其值越大死区也越大。
决定了整体数据权值的大小和权值曲线的斜率。其值越大权值整体越偏小同时曲线的斜率也越平缓。
这里限定
关于
的取值对曲线的影响,下图可以给出了一个直观的印象。
delta取值对曲线的影响:
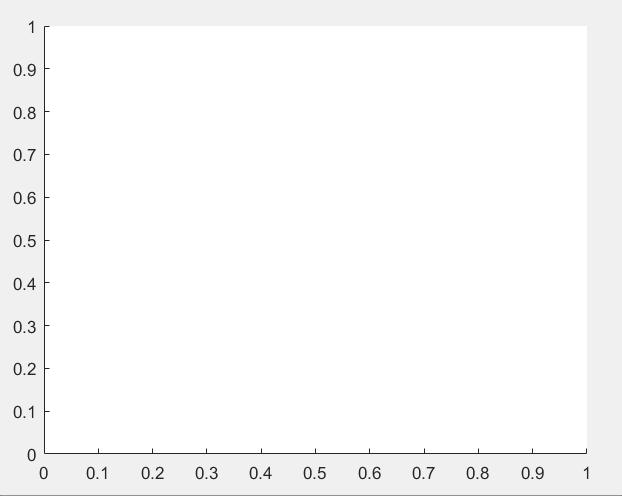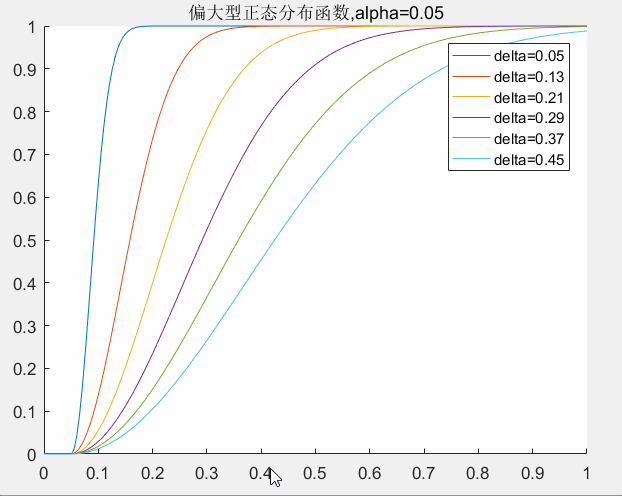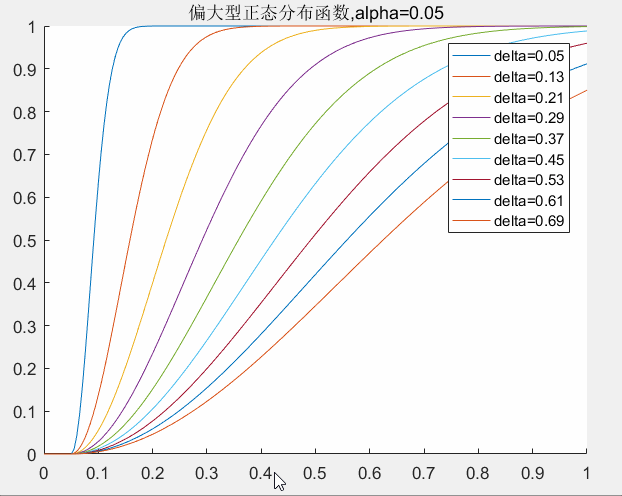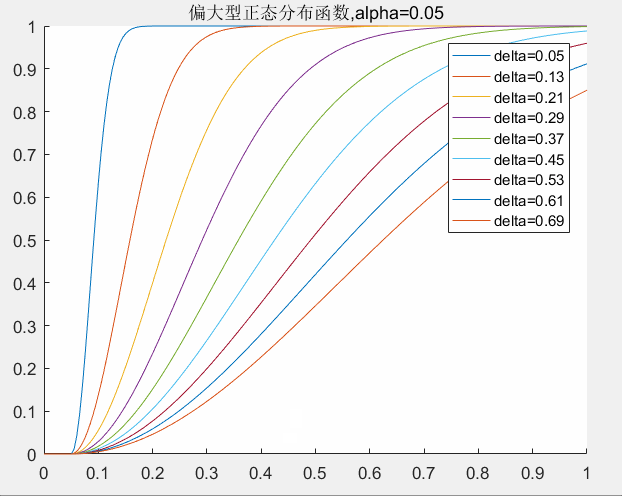
alpha取值对曲线的影响:
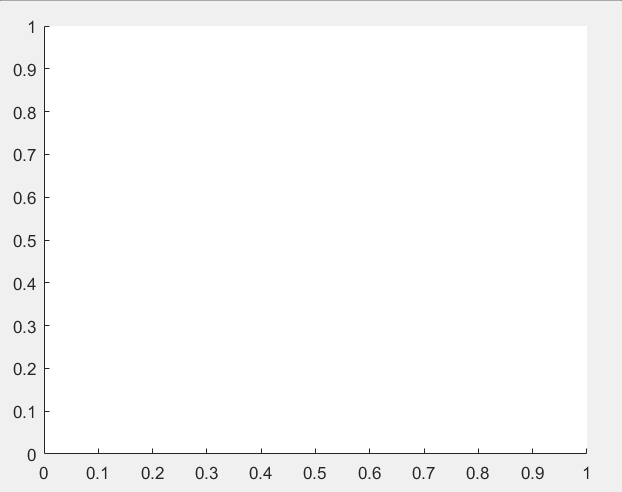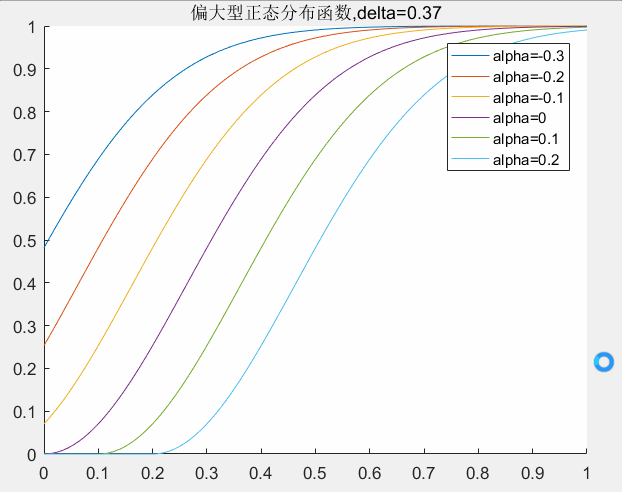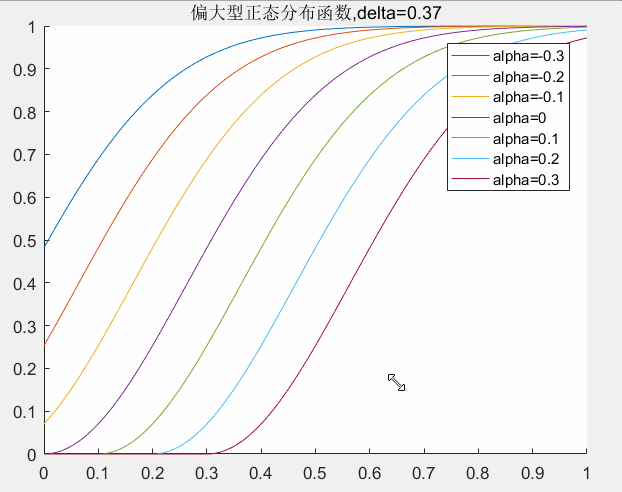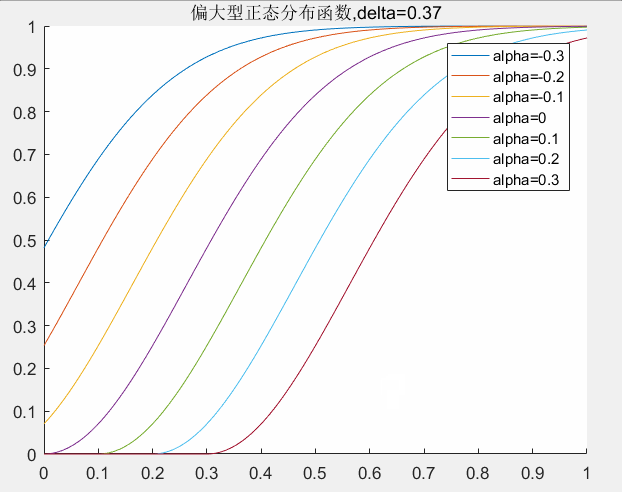
对应matlab代码如下所示:
clear
clc
alpha = 0.05;
hold on
title('偏大型正态分布函数,alpha=0.05')
i = 1;
for delta=0.05:0.08:0.7
x=linspace(0,1,200);
y = x;
y(x<=alpha) = 0;
index = (x>alpha);
y(index) = 1-exp(-((x(index)-alpha)./delta).^2);
plot(x,y)
strLe{i}=['delta=',num2str(delta)];
i=i+1;
legend(strLe)
pause(1);
end
figure
hold on
title('偏大型正态分布函数,delta=0.37')
i = 1;
delta=0.37;
for alpha=-0.3:0.1:0.3
x=linspace(0,1,200);
y = x;
y(x<=alpha) = 0;
index = (x>alpha);
y(index) = 1-exp(-((x(index)-alpha)./delta).^2);
plot(x,y)
if abs(alpha)< 0.0001
alpha = 0;
end
strLe1{i}=['alpha=',num2str(alpha)];
i=i+1;
legend(strLe1)
pause(1);
end
下面matlab代码验证C++算法是否正确。可以将C++计算结果和其进行比较。
clear
clc
alpha = 0.05;
delta = 0.45;
x = [0.25 1/3 0.4;0.625 2/3 0.7;1 1 1];
wX = 1-exp(-((x-alpha)./delta).^2);
wX(x>=1) = 1
4.2 S型分布函数参数的确定
和偏大型分布函数一样,在S型分布函数中也有两个参数(a,b)需要确定,这里a和b的意义比较明显a是权值左边的控制点,b是右边的控制点。中间是S型曲线,两边都是死区。下图给出参数a,b取值对权值的影响。这里a,b的取值范围为:

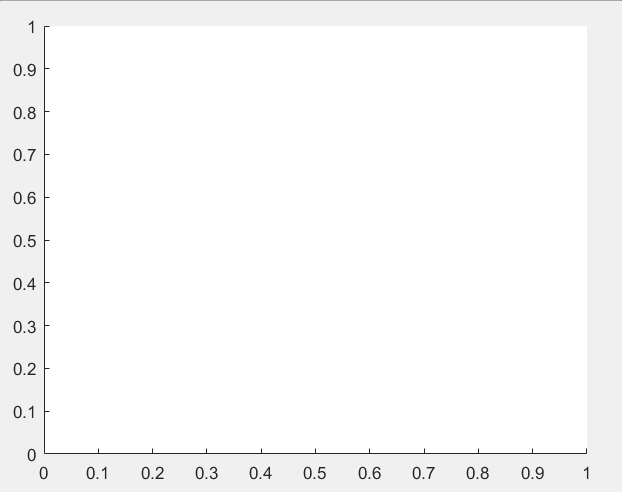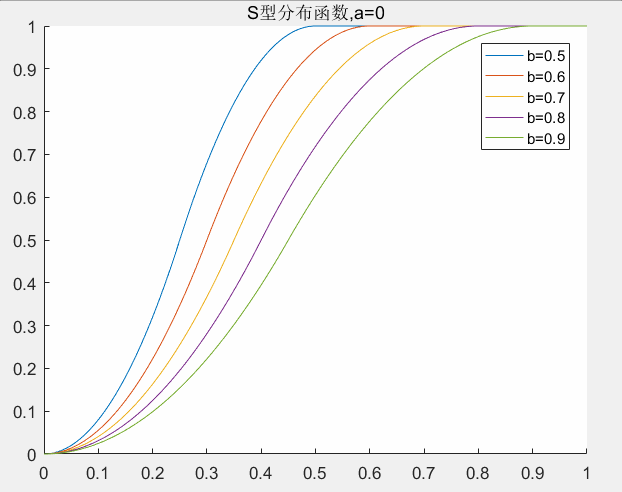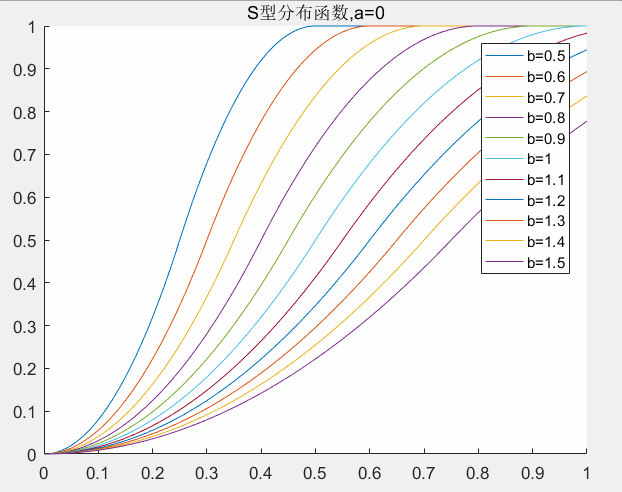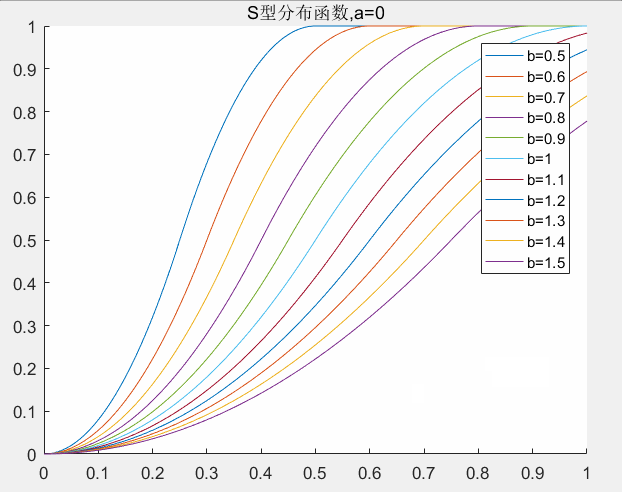
对应matlab代码:
clear
clc
b = 1;
x = linspace(0,1,200);
hold on
title('S型分布函数,b=1')
i = 1;
for a=-0.5:0.1:0.5
c = (a+b)/2;
y = x;
y(x<a) = 0;
index = (x>=a)&(x<=c);
y(index)= 2*((x(index)-a)/(b-a)).^2;
index = (x>c)&(x<=b);
y(index) = 1-2*((x(index)-b)/(b-a)).^2;
y(x>b) = 1;
strLe{i} = ['a=',num2str(a)];
i = i+1;
plot(x,y)
legend(strLe);
pause(1);
end
figure
a = 0;
x = linspace(0,1,200);
hold on
title('S型分布函数,a=0')
i = 1;
for b=0.5:0.1:1.5
c = (a+b)/2;
y = x;
y(x<a) = 0;
index = (x>=a)&(x<=c);
y(index)= 2*((x(index)-a)/(b-a)).^2;
index = (x>c)&(x<=b);
y(index) = 1-2*((x(index)-b)/(b-a)).^2;
y(x>b) = 1;
strLe{i} = ['b=',num2str(b)];
i = i+1;
plot(x,y)
legend(strLe);
pause(1);
end
下面matlab代码用以验证C++算法是否正确,可以通过设置相同的a,b和矩阵参数来进行对比。
clear
clc
a = 0;
b = 1;
x = [0.25 1/3 0.4;0.625 2/3 0.7;1 1 1];
c = (a+b)/2;
y = x;
y(x<a) = 0;
index = (x>=a)&(x<=c);
y(index)= 2*((x(index)-a)/(b-a)).^2;
index = (x>c)&(x<=b);
y(index) = 1-2*((x(index)-b)/(b-a)).^2;
y(x>b) = 1;
5 加权评估
在对数据进行一致化、无量纲化并且确定权值后我们就可以对系统进行加权评估了。加权评估类(AddWeight)在使用时有四个关键属性:
- 测量矩阵(MeaMat)
- 权值矩阵(WeightMat)
- 数据处理方向(Dir)
- 是否线性加权(IsLin)
测量矩阵(MeaMat):必须要设置的选项,默认测量矩阵每一行为一个带评价系统,每一列为一个评价指标。且这个测量矩阵必须是经过一致化和无量纲化后的矩阵。当然可以通过设置Dir属性改变矩阵的行列表达意义。
权值矩阵(WeightMat):一般也是要设置的选项,但是也可以不设置,默认所有数据的权值都为1.如果权值为一个元素个数和评价指标数相同的向量(行或列),那么则是固定权值进行加权,对应元素的值代表了评价指标的权值。如果权值为一个和测量矩阵同维数的矩阵,则为动态权值,每一个数据的权值在权值矩阵上的对应位置上。
数据处理方向(Dir):数据处理方向用来设置测量矩阵行列表示的意义,默认为E_MatrixDir::ColumnDir,即行表示评价系统列表示评价指标。也可以通过设置E_MatrixDir::RowDir来改变行和列的意义。一般此参数不用设置。
是否线性加权(IsLin):是用来表示评价系统的加权方式,默认为线性加权即对于权值和数据相乘然后所有指标求和。这里还提供了一种非线性加权的方式,即将系统所有数据的权值次方相乘。一般此参数也不用设置,使用默认参数即可。
这里在建立加权评估对象的时候提供了三种构造函数,分别是不带参数的构造函数,带测量矩阵的构造函数和带测量矩阵和加权矩阵的构造函数。如果使用的是不带测量矩阵的构造函数建立对象,我们可以在之后通过setXXX()来进行设置,其中XXX为上面提到的4个参数。下面就以经过居中型到极大型和归一化处理的矩阵作为测量矩阵,以其经过S分布函数处理过的矩阵作为权值矩阵来测试加权评估(省略的前面重复了的代码)。
cout << "加权" << endl;
try
{
AddWeight<Matrix3d> aw;
aw.SetMea(myMatrix);
aw.SetWei(weight);
//aw.SetIsLin(IsLinear::Nonlinear);
typedef typename AddWeight<Matrix3d>::ResultS ResultS;
//vector<ResultS> res = aw.StartEval(); //可以直接返回结果
aw.StartEval();
vector<ResultS> res = aw.GetResult(); //也可以使用get方法
cout << "归一化矩阵加权结果为:" << endl;
for (unsigned int i = 0; i < res.size(); ++i)
cout << "第"<<i<<"个系统的评价结果为:"<<res[i].EvalValue << " 排名: "<<res[i].Rank<<endl;
cout << endl;
cout << aw.GetMea().size() << endl;
}
catch (CompEvalFail& cef)
{
cout << cef.GetMessage() << endl;
}
执行结果如下:
归一化
0.25 0.333333 0.4
0.625 0.666667 0.7
1 1 1
...
S型分布
0.125 0.222222 0.32
0.71875 0.777778 0.82
1 1 1
加权
归一化矩阵加权结果为:
第0个系统的评价结果为:0.233324 排名: 3
第1个系统的评价结果为:1.54174 排名: 2
第2个系统的评价结果为:3 排名: 1
可以使用如下matlab代码进行验证:
clear
clc
weight = [0.125 0.22222 0.32;0.71875 0.777777 0.82;1 1 1];
mat = [0.25 0.33333 0.4;0.625 0.6666 0.7;1 1 1];
result = sum(weight.*mat,2)
这里定义了一个简单的用以处理异常的类CompEvalFail,该类只有一个方法就是获取异常的字符串。比如如果出现设置的权值矩阵维数不对,捕获该异常后,调用GetMessage方法就会输出相关信息。返回结果是一个vector类型,其模板参数为一个结构体。结构体第一个成员EvalValue为评估值,第二个成员为系统根据评估值排序的对应排名。
最终的测试结果如下:

ps:这个算法的实现是我自学C++以来第一个上手实现的算法,最开始使用Eigen时没有看官方的使用矩阵作为函数参数的介绍。这里将构建矩阵所需的三个最基本的模板参数直接传递到我的函数中,使用起来非常麻烦。直到使用动态加权时才看到官方关于矩阵作为函数怎么处理。为了不实例化对象就能使用函数,这里使用了静态方法。代码中也存在很大重复的代码,比如检查矩阵的合法性。虽然在开始编写的时候出现了很多问题,但是最后编写AddWeight类的时候基本已经对C++有一定的了解了。而之前出现的问题也懒得回去重构了。
虽然代码看上去一坨屎,前面的文档也写的很马虎,最开始还画画UML,但后来发现类在编程实现的时候有很大的改变,到最后也懒得画了。最关键的是可能还有很多的bug没有发现。虽然毛病很多,但是在这一个多星期断断续续编写的1500行代码中还是学到很多C++中常用的操作的,比如模板的使用方式有了更深刻的理解,同时看了看Eigen的源码也很有启发。包括typename的使用和enum的特殊使用(利用enum值可以一样的特性用其定义变量)等。总得来说从开始学习C++以来的不到一个月时间能学习这么多知识对自己的进步还是很满意的,毕竟是断断续续边工作边学习。
在学习C++的过程中我发现了,还是高级语言用着舒服啊,matlab矩阵相乘是真方便,画图也是真方便。这个综合评价模型的例子之前参加数学建模时用matlab一个多小时搞定的算法,用C++边学习,边找矩阵库,边学习矩阵库,整了快用了两个星期。不过要在真的要在嵌入式平台实现算法还真是离不开C++。看来以后要慢慢熟悉这种算法的开发流程——理论推导、matlab验证到C++嵌入式平台实现。