机器学习-EM算法-pLSA模型笔记

pLSA模型--基于概率统计的pLSA模型(probabilistic Latent Semantic Analysis，概率隐语义分析)，增加了主题模型，形成简单的贝叶斯网络，可以使用EM算法学习模型参数。概率潜在语义分析应用于信息检索，过滤，自然语言处理，文本的机器学习或者其他相关领域。

D代表文档，Z代表主题(隐含类别)，W代表单词；
　　P(d_i)表示文档d_i的出现概率，
　　P(z_k|d_i)表示文档d_i中主题z_k的出现概率，
　　P(w_j|z_k)表示给定主题zk出现单词w_j的概率。
每个主题在所有词项上服从多项分布，每个文档在所有主题上服从多项分布。
整个文档的生成过程是这样的：
　　以P(d_i)的概率选中文档d_i；
　　以P(z_k|d_i)的概率选中主题z_k；
　　以P(w_j|z_k)的概率产生一个单词w_j。
观察数据为(d_i,w_j)对，主题z_k是隐含变量。
(d_i,w_j)的联合分布为

 
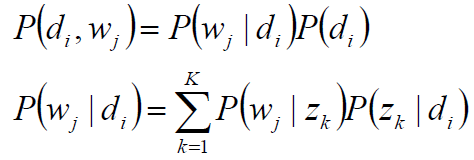
而P(w_j|z_k)，P(z_k|d_i)对应了两组多项分布，而计算每个文档的主题分布，就是该模型的任务目标。

最大似然估计：wj在di中出现的次数n(d_i,w_j)

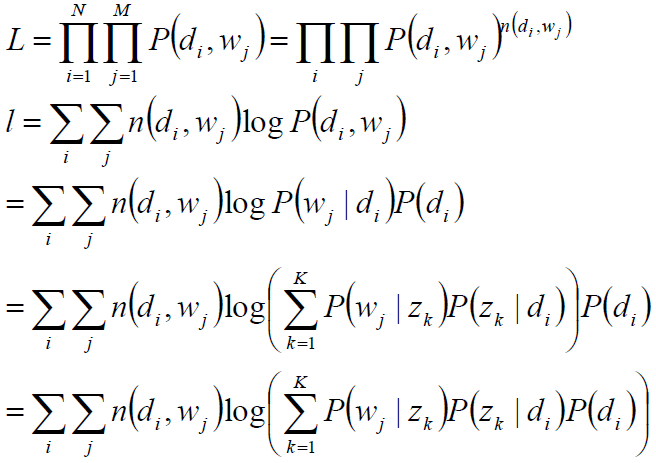
目标函数分析:

观察数据为(d_i,w_j)对，主题zk是隐含变量。

目标函数:

未知变量/自变量P(w_j|z_k)，P(z_k|d_i)

　　1) 使用逐次逼近的办法：假定P(z_k|d_i)、P(w_j|z_k)已知，求隐含变量z_k的后验概率；

　2) 在(d_i,w_j,z_k)已知的前提下，求关于参数P(z_k|d_i)、P(w_j|z_k) 的似然函数期望的最大值，得到最优解P(z_k|d_i)、P(w_j|z_k) ，带入上一步，从而循环迭代,即：EM算法。

求隐含变量主题zk的后验概率:

　　假定P(z_k|d_i)、P(w_j|z_k)已知，求隐含变量z_k的后验概率；

　　　

　　在(d_i,w_j,z_k)已知的前提下，求关于参数P(z_k|d_i)、P(w_j|z_k) 的似然函数期望的最大值，得到最优解P(z_k|d_i)、P(w_j|z_k) ，带入上一步，从而循环迭代。

关于参数P(z_k|d_i)、P(w_j|z_k)  的似然函数期望

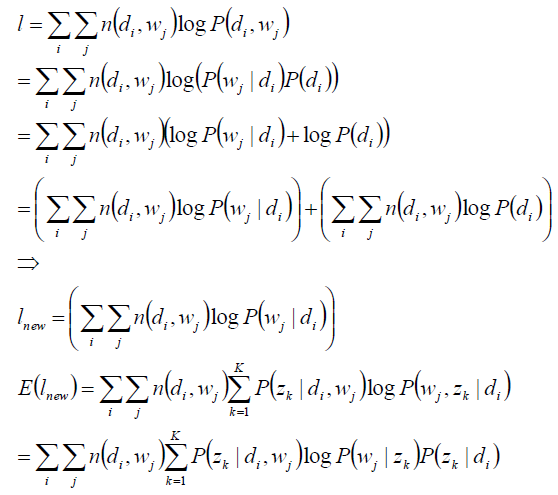
完成目标函数的建立：

关于参数P(z_k|d_i)、P(w_j|z_k) 的函数E，并且，带有概率加和为1的约束条件：

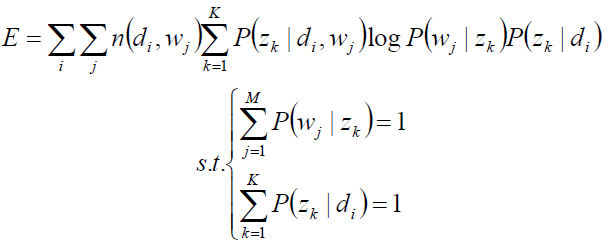
显然，这是只有等式约束的求极值问题，使用Lagrange乘子法解决。

目标函数的求解：

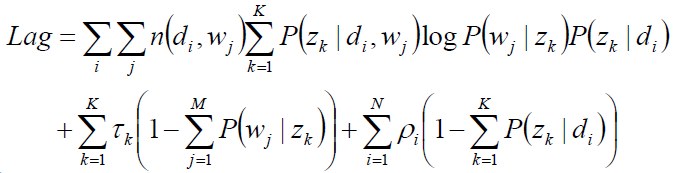
求驻点：

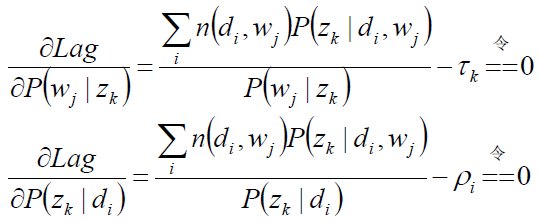
分析第一个等式：

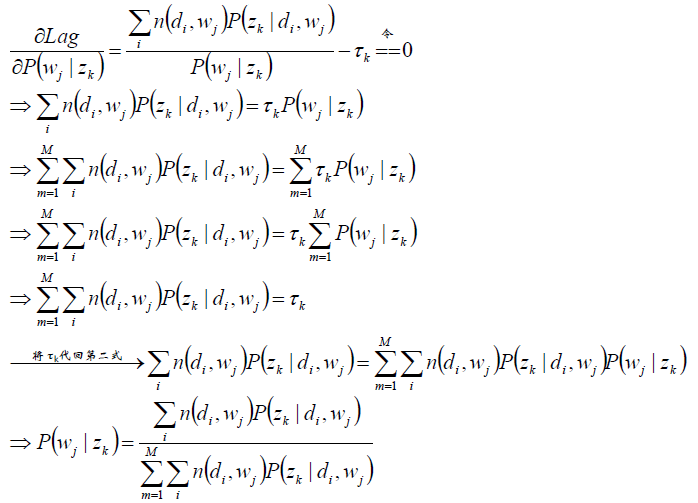
同理分析第二个等式：

求极值时的解——M-Step：

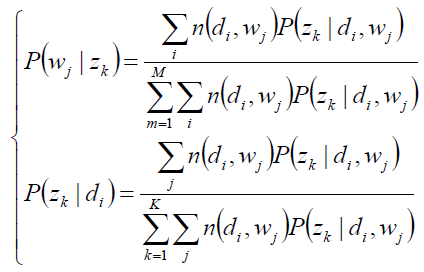
E-step（z_k的后验概率）：

pLSA的总结：

　　1）pLSA应用于信息检索、过滤、自然语言处理等领域，pLSA考虑到词分布和主题分布，使用EM算法来学习参数。
　2）虽然推导略显复杂，但最终公式简洁清晰，很符合直观理解，需用心琢磨；此外，推导过程使用了EM算法，也是学习EM算法的重要素材。