1. 一维随机变量
通俗的讲,随机变量就是指数轴上的数。
一个事件的结果(样本)可以用文字或者字母来表示,但这样并不直观,也无法计算,所以我们将它们一一映射到数轴上,于是数轴上的数就有了
不同的含义,我们称为随机变量。几个符号解读:
1)$x$ $in$ 随机变量全体。它代表一般随机变量,表示横轴上的任一个数。
2)$X$ $in$ 映射后样本空间中的随机变量。它代表样本随机变量,具有一般性,可以表示映射后样本空间中的任一个样本。
3)$omega$ $in$ 原来的样本空间 $Omega$。它代表样本变量,具有一般性,可以表示原来样本空间中的任一个样本。
$$X = f(omega), omega in Omega$$
4)$x_{i}$、$x_{k}$、$y_{j}$ 等表示具体的确定的一个样本,不具有一般性,是 $X$ 的可能取值,如样本空间可以表示为 $left { x_{1}, x_{2},x_{3},x_{4} ight }$。
5)$X = x_{1}$、$x_{1} leq X leq x_{2}$、$X leq x$ 等都表示事件。一个样本是一个基本事件,样本的集合称为事件。$X = x_{1}$ 指样本 $x_{1}$ 发生,
这里只有一个样本,所以它是基本事件。$x_{1} leq X leq x_{2}$ 指样本落在 $x_{1}$ 和 $x_{2}$ 之间,很明显它是一个样本的集合。
6)如何表示事件发生的概率呢?P{事件} 或者 P(事件),如 $P(X = x_{1})$、$Pleft { x_{1} leq X leq x_{2} ight }$、$Pleft { X leq x ight }$。
一般来讲用()来表示基本事件的概率,{}表示集合事件的概率。
1)离散型随机变量:$X$ 的可能取值为有限多个或可数无穷个,$y$ 轴表示某个样本发生的概率,比如

映射后的样本空间里有1、3、7,所以 $X$ 的可能取值为1、3、7,$Pleft { X = 1 ight } = 0.2$...这个图称为概率分布,也可以写成数学形式
$$Pleft { X = x_{k} ight } = p_{k},k = 1,2,3,...$$
分布函数:考虑事件:样本变量 $X$ 落在区间 $(-infty,x]$。分布函数便是求这个事件的概率:
$$F(x) = Pleft { X leqslant x ight } = sum_{x_{k} leq x}^{}p_{k},k=1,2,3,...$$
用 $x_{k}$ 来遍历满足条件的所有样本,相当于一层 $for$ 循环,对于离散型随机变量,概率求和就是对应的 $y$ 值累加。
概率分布是已知的,是静态的,一般针对不同的概率分布,很难得到一个统一的 $F(x)$ 的表达式,很多时候需要对 $x$ 的范围进行讨论,得到不同区间的表达式。
$F(x)$ 的性质:
a. $0 leq F(x) leq 1$
b. $F(+infty) = 1, F(-infty) = 0$
2)连续型随机变量:$X$ 的可能取值无法一一列举出来,在某一区间内可取无穷个。离散型随机变量是点概率,那连续型随机变量
能否也采用概率分布的那种形式呢?
比如在某个区间 $[0,1]$ 内取一个点,由于 $X$ 在该区间内的可能取值有无穷个,所以可计算得到该点的概率为 0。这并不合理。
因此,对于连续型随机变量,我们不研究它取某个特定值的概率,而研究样本 $X$ 落在某一区间上的概率,用对应的面积表示概率。
很明显,对一个趋近于某一点的区间内求面积也是趋于 0 的,所以这种形式是合理的。
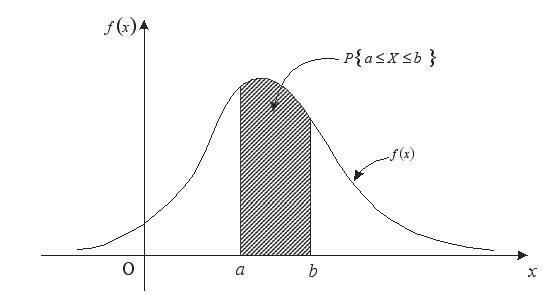
这个图称为 $X$ 的概率密度(对应离散的概率分布),这里求概率便不是 $y$ 轴的值了,而是概率密度函数曲线下的面积(如阴影部分面积)。
这里的概率密度就没办法写出它的数学形式了,将它记为 $f(x)$,而不是像离散那样的形式 $Pleft { X = x ight }$ 。
分布函数:连续型随机变量分布函数也是求事件:样本变量 $X$ 落在区间 $(-infty,x]$ 的概率:
$$F(x) = Pleft { X leqslant x ight } = int_{-infty}^{x}f(t)dt,-infty < x < +infty$$
这里相当于用变量 $t$ 来遍历,所求概率和是概率密度函数和区间围成的面积。
$F(x)$ 的性质:
a. $0 leq F(x) leq 1$
b. $F(+infty) = 1, F(-infty) = 0$
c. $Pleft { x_{1} < X leq x_{2} ight } = int_{x_{1}}^{x_{2}}f(t)dt,x_{1} < x_{2}$
2. 二维随机变量
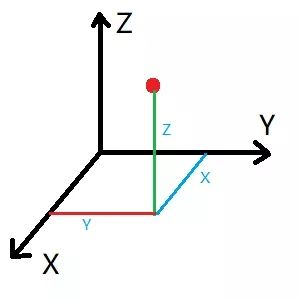
将一维随机变量类比到二维,此时坐标系由平面变成空间。
$(x,y)$ $in$ 随机变量全体,$(X,Y)$ $in$ 映射后样本空间中的随机变量(即 $(X,Y)$ 是映射后的样本随机变量,具有一般性),$omega$ $in$ 原来的样本空间 $Omega$,
$$X = f_{1}(omega), Y = f_{2}(omega), omega in Omega$$
从这个式子我们可以看到,两个不同函数 $f_{1}$,$f_{2}$ 是作用于同一个样本 $omega$。
1)离散型随机变量:$(X,Y)$ 的可能取值为有限多个或可数无穷个,$z$ 轴表示某个样本发生的概率,比如
这个图称为联合概率分布,在空间中是很多离散的点,也可以写成数学形式
$$Pleft { X = x_{i}, Y = y_{j} ight } = p_{ij}, i,j=1,2,3...$$
联合分布函数:考虑事件:样本变量 $(X,Y)$ 落在平面 $(-infty,x] cap (-infty,y]$,联合分布函数便是求这个事件的概率:
$$F(x,y) = Pleft { X leqslant x,Y leqslant y ight } = sum_{x_{i} leq x}^{}sum_{y_{j} leq y}^{}p_{ij}, i,j=1,2,3,...$$
用 $x_{i}$,$y_{j}$ 来遍历所有满足条件的样本,相当于 2 层 $for$ 循环,对于离散型随机变量,概率和即为 $(X,Y)$ 对应的 $z$ 值求和。
$F(x,y)$ 性质:
a. 对于任意实数 $x_{1}$,$x_{2}$,$y_{2}$,$y_{2}$,($x_{1} leq x leq x_{2}$,$y_{1} leq y leq y_{2}$),下述不等式恒成立
$$Pleft { x_{1} leq X leq x_{2}, y_{1} leq Y leq y_{2} ight } = F(x_{1},y_{1}) + F(x_{2},y_{2}) - F(x_{1},y_{2}) -F(x_{2},y_{1})$$
可以发现,一个概率分布对应一个分布函数,如联合概率分布/联合分布函数,下面来介绍另外 2 对。
- 边缘概率分布/边缘分布函数
边缘分布即随机向量中分量各自的概率分布。
$$Pleft { X = x_{i} ight } = Pleft { X = x_{i}, Y < +infty ight } = sum_{j=1}^{+infty}Pleft { X = x_{i}, Y = y _{j} ight }, i=1,2,3...$$
$$Pleft { Y = y_{j} ight } = Pleft { X < +infty, Y = y_{j} ight } = sum_{i=1}^{+infty}Pleft { X = x_{i}, Y = y _{j} ight }, j=1,2,3...$$
边缘分布函数形式如下:
$$F_{X}left ( x ight ) = Fleft ( x, +infty ight ) = Pleft { X leq x, Y < +infty ight } = sum_{x_{i} leq x}^{}sum_{j=1}^{+infty}Pleft { X = x_{i}, Y = y _{j} ight }, i=1,2,3...$$
$$F_{Y}left ( y ight ) = Fleft ( +infty, y ight ) = Pleft { X < +infty, Y leq y ight } = sum_{y_{j} leq y}^{}sum_{i=1}^{+infty}Pleft { X = x_{i}, Y = y _{j} ight }, j=1,2,3...$$
相当于两层循环,如果求 $X$ 的边缘分布,则内层对 $Y$ 做全范围的遍历。
- 条件概率分布/条件分布函数
考虑在其中一个随机变量取得固定值的条件下,另一随机变量的概率分布,这样得到的 $X$ 或 $Y$ 的概率分布叫做条件概率分布,数学形式如下
$$Pleft { X = x_{i} | Y = y_{j} ight } = frac{Pleft { X = x_{i},Y = y_{j} ight }}{Pleft { Y = y_{j} ight }}, i = 1,2,3,...$$
$$Pleft { Y = y_{j} | X = x_{i} ight } = frac{Pleft { X = x_{i},Y = y_{j} ight }}{Pleft { X = x_{i} ight }}, j = 1,2,3,...$$
当随机变量 $Y$ 固定后,就退化为一维的情况,所以条件分布函数求的是另一个随机变量 $X$ 在区间 $(-infty,x]$ 发生时的概率和,即
$$Pleft { X leq x | Y = y_{j} ight } = frac{Pleft { X leq x,Y = y_{j} ight }}{Pleft { Y = y_{j} ight }} = sum_{x_{i} leq x}^{}Pleft { X = x_{i} | Y = y_{j} ight }, i = 1,2,3,...$$
$$Pleft { Y leq y | X = x_{i} ight } = frac{Pleft { Y leq y,X = x_{i} ight }}{Pleft { X = x_{i} ight }} = sum_{y_{j} leq y}^{}Pleft { Y = y_{j} | X = x_{i} ight }, j = 1,2,3,...$$
用 $x_{i}$ 来遍历满足条件的样本 $X$,相当于一层 $for$ 循环。
2)连续型随机变量:$(X,Y)$ 的可能取值无法一一列举出来,在某一区间内可取无穷个。
同理,对于连续型随机变量,我们不研究它取某个特定值的概率,而研究样本 $(X,Y)$ 落在某一平面上的概率,用对应的体积表示概率。
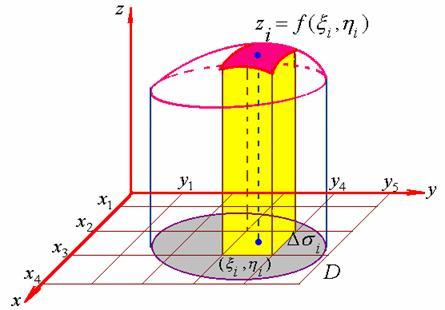
这个图称为 $(X,Y)$ 的联合概率密度(对应离散的联合概率分布),这里求概率便不是 $z$ 轴的值了,而是概率密度函数曲面下的体积(如黄色部分体积)。
联合概率密度也无法写出数学形式,将它记为 $f(x,y)$,而不是像离散那样的形式 $Pleft { X = x_{i}, Y = y_{i} ight }$。
联合分布函数:也是求事件:样本变量 $(X,Y)$ 落在平面 $(-infty,x] cap (-infty,y]$ 的概率(体积):
$$F(x,y) = Pleft { X leqslant x,Y leqslant y ight } = int_{-infty}^{x}int_{-infty}^{y}f(u,v)dudv, -infty < x,y < +infty$$
$F(x,y)$ 性质:
a. 对于任意实数 $x_{1}$,$x_{2}$,$y_{2}$,$y_{2}$,($x_{1} leq x leq x_{2}$,$y_{1} leq y leq y_{2}$),下述不等式恒成立
$$Pleft { x_{1} leq X leq x_{2}, y_{1} leq Y leq y_{2} ight } = F(x_{1},y_{1}) + F(x_{2},y_{2}) - F(x_{1},y_{2}) -F(x_{2},y_{1})$$
- 边缘概率密度/边缘分布函数
每个变量各自的概率密度函数即为随机变量 $(X,Y)$ 关于 $X$ 或者 $Y$ 各自的概率密度函数,是一元函数。
$$f_{X}(x) = int_{-infty}^{+infty}f(x,y)dy$$
$$f_{Y}(y) = int_{-infty}^{+infty}f(x,y)dx$$
边缘分布函数可以通过对边缘概率密度积分得到:
$$F_{Y}(y) = F(+infty,y) = int_{-infty}^{+infty}int_{-infty}^{y}f(u,v)dudv = int_{-infty}^{y}[int_{-infty}^{+infty}f(u,v)du]dv = int_{-infty}^{y}f_{Y}(v)dv$$
$$F_{X}(x) = F(x,+infty) = int_{-infty}^{x}int_{-infty}^{+infty}f(u,v)dudv = int_{-infty}^{x}[int_{-infty}^{+infty}f(u,v)dv]du = int_{-infty}^{x}f_{X}(u)du$$
- 条件概率密度/条件分布函数
对于连续型随机变量,是不讨论点概率的,即$Pleft { Y = y ight } = 0$ 或 $Pleft { X = x ight } = 0$。以 $Y = y$ 为例,则
$Pleft { X leq x | Y = y ight } = 0$ 是无意义的,这里是利用极限的方法来引入条件分布函数的。
给定任意一个固定的整数 $varepsilon$,则 $Pleft { y-varepsilon < Y leq y+varepsilon ight } > 0$。
$$F_{X|Y}(x|y) = Pleft { X leq x | Y = y ight } = lim_{varepsilon ightarrow 0^{+}}Pleft { X leq x | y-varepsilon < Y leq y+varepsilon ight } = lim_{varepsilon ightarrow 0^{+}}frac{Pleft { X leq x, y-varepsilon < Y leq y+varepsilon ight }}{Pleft { y-varepsilon < Y leq y+varepsilon ight }}$$
根据联合分布函数的性质,继续推导:
$$= lim_{varepsilon ightarrow 0^{+}}frac{F(x,y+varepsilon) - F(x,y-varepsilon)}{F_{Y}(y+varepsilon)-F_{Y}(y-varepsilon)} = lim_{varepsilon ightarrow 0^{+}} frac{frac{F(x,y+varepsilon) - F(x,y-varepsilon)}{2varepsilon}}{frac{F_{Y}(y+varepsilon)-F_{Y}(y-varepsilon)}{2varepsilon}}$$
由偏导数和导数的定义知:
$$=frac{frac{partial F(x,y)}{partial y}}{frac{dF_{Y}(y)}{dy}} = frac{frac{partial }{partial y}[int_{-infty}^{y}int_{-infty}^{x}f(u,v)dudv]}{f_{Y}(y)} = frac{int_{-infty}^{x}f(u,y)du}{f_{Y}(y)} = int_{-infty}^{x}frac{f(u,y)}{f_{Y}(y)}du$$
明显,条件概率密度和条件分布函数都是关于 $x$ 和 $y$ 的二元函数。
对于一切 $f_{Y}(y) > 0$ 的 ,在给定 $Y = y$ 的条件下,$X$ 的条件概率密度和条件分布函数分别为:
$$f_{X|Y}(x|y) = frac{f(x,y)}{f_{Y}(y)}, f_{Y}(y) > 0$$
$$F_{X|Y}(x|y) = int_{-infty}^{x}f_{X|Y}(u|v)du = int_{-infty}^{x}frac{f(u,y)}{f_{Y}(y)}du$$
对于一切 $f_{X}(x) > 0$ 的 ,在给定 $X = x$ 的条件下,$Y$ 的条件概率密度和条件分布函数分别为:
$$f_{Y|X}(y|x) = frac{f(x,y)}{f_{X}(x)}, f_{X}(x) > 0$$
$$F_{Y|X}(y|x) = int_{-infty}^{y}f_{Y|X}(v|u)dv = int_{-infty}^{y}frac{f(x,v)}{f_{X}(x)}dv$$