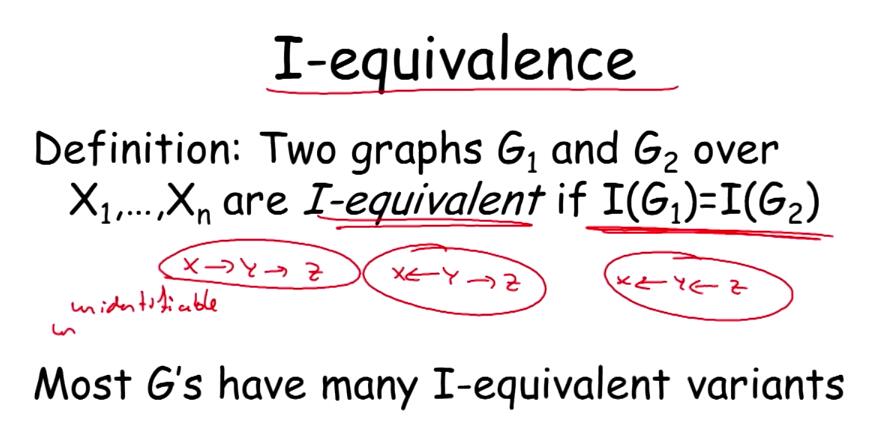2、概率图模型: Markov Random Fields

　　上一篇的末尾讲到了表现性的问题，贝叶斯网络不能完全表现出某些概率分布特征，而马尔科夫网络有更好的表现性，马尔科夫网络是无向图模型（UGM）。

一、Factors（因子）

　　每个因子可以是一个函数，也可以是一个表，表示其中的variables之间的关系。表示为Φ（X1，X2，...，Xk）。

　　factor的范围scope = {X1，X2，...，Xk}，之前的概率分布P(A,B,C)均是factor。

　　每个factor中包含了很多variables，每个variables也可能有很多的取值，对应关系为：factor——>variables——>values。

二、配对马尔科夫网络（Pairwise Markov Network）

　　是一个有节点X1 , ... , Xn，和边 Xi - Xj 的无向图，和factor Φ_ij(Xi,Xj) 相关联，每个factor只表达两个节点的对应关系。

　　 对于MNs中的factor的理解，下面的例子：

 

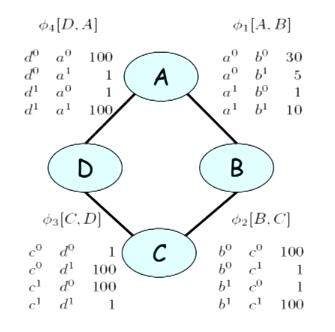
 图1（取自coursera PGM公开课）

　　其中A,B,C,D是四位同学，图表示的是他们之间互相学习的关系，相互连线表示两个人能共同学习，而factor  Φ_i  表示他们之间的学习效率，每个factor中的variable都有两个取值——0和1，表示的是学习的方式。以C,D为例，两个人在variable的取值相同的情况下， Φ3[C,D]的值都是1，说明两个人在学习方法相同的情况下学习效率比较低；而在variable取值不同的情况下，Φ3[C,D]的值都是100，说明两个人在学习方法不一样的情况下，学习的效率比较高。整个的分布情况也可以表示成如下：

 

 

 

二、一般吉布斯分布（General Gibbs Distribution）

　　现在假设一个全链接的成对马尔可夫网络，有 X1，...，Xn 个variables，每一个variable中有 d 个values，那么所有的组合一共有多少种情况，最终会得到多少参数（每一种情况的结果）?

　　 先来看对于 X 之间的链接一共会有多少种情况，每个 X 都可能会和其他 n-1 个进行链接，也就是说数量级是 O（n²），每两个 X 之间的values可能的组合是  O（d²），那么整个情况的数量级便是 O（n²d²）。

　　 再来考虑条件概率分布的情况，单说贝叶斯网络的情况，贝叶斯网络中的组合情况在上一篇博客中提到，最终的组合数量级是  O（dⁿ）>> O（n²d²），由此可见，配对马尔科夫网络所表现出来的图中变量的分布情况并不是很全面，最好是在马尔科夫网络中加入条件概率来增加网络的表现度，首先第一步要做的便是将马尔科夫网络中的分布转换成概率分布，于是便有了一般吉布斯分布。

　　吉布斯分布：对于如下的一个factor，是一个k个factor的集合，Φ 是一个马尔科夫网络

　

　　 那么该网络中的分布可以表示为：

 

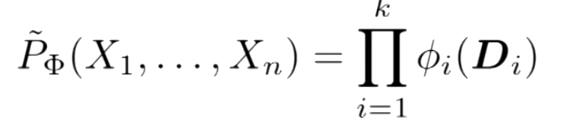
　　 在P的上面加上的波浪号，表示该分布不是概率分布模型，从上面的例子中可以看出，还并不是一个概率分布。要将其变成概率分布，则需要对所有的 Φi（Di）进行求和，每一个  Φi（Di）所占总数的多少，用其和所得求和相除即可，这边是标准化操作。

 

 

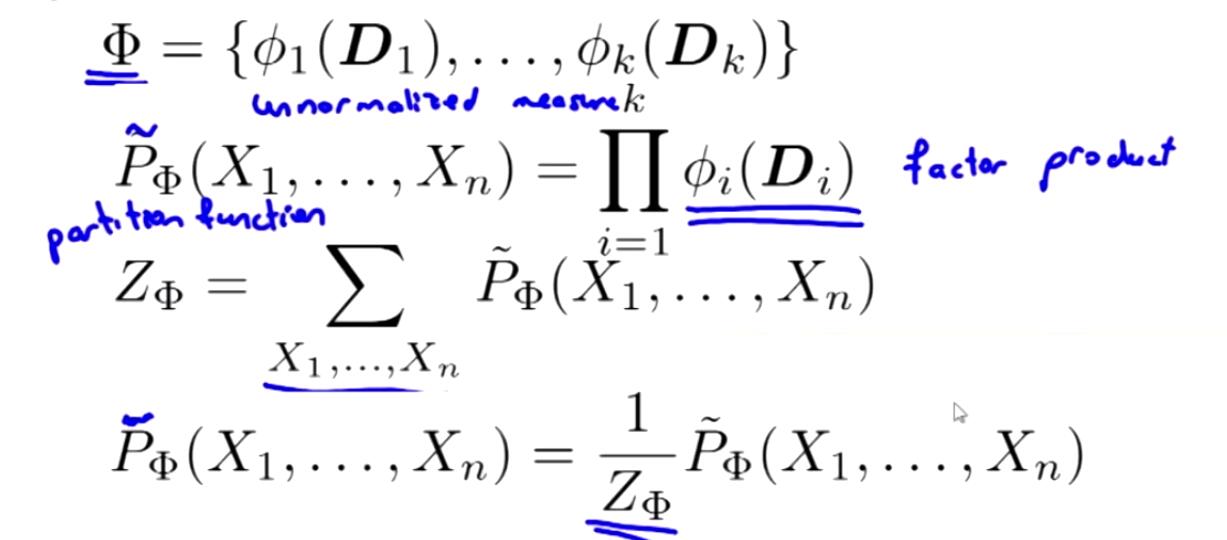
三、条件随机场（Conditional Random Field）

　　之前的马尔科夫网络都是 X 之间的成对对应关系，但是对于一些实际应用中，例如图像识别中，通过一小块区域中的像素分布，推测出该小块区域是什么图形（草地、山等），可以建立如下的概率图：

 

图2

 

　　Ci 表示的是左图中的一小块区域的标签，如草地、牛等等，其中的 Xi1...Xik 则表示的是该区域内的颜色分布，实际情况中得到的是 Xi1...Xik ，要根据这些来判断出该块区域的 Ci ，那么需要用到条件概率来进行判断（对于为什么对于该问题用条件随机场要优于贝叶斯概率图模型，教程中的解释没有完全读懂，这里先留下一个坑，结合后面的知识回来再填这个坑），在之前的马尔可夫网络加上条件概率分布。

　　整个推导的过程如下，比较好理解，求出 X 的边缘分布，并用 X,Y 的联合分布来除以 X 的边缘分布，得到的表示标准化之后的 Y基于X的条件概率分布。

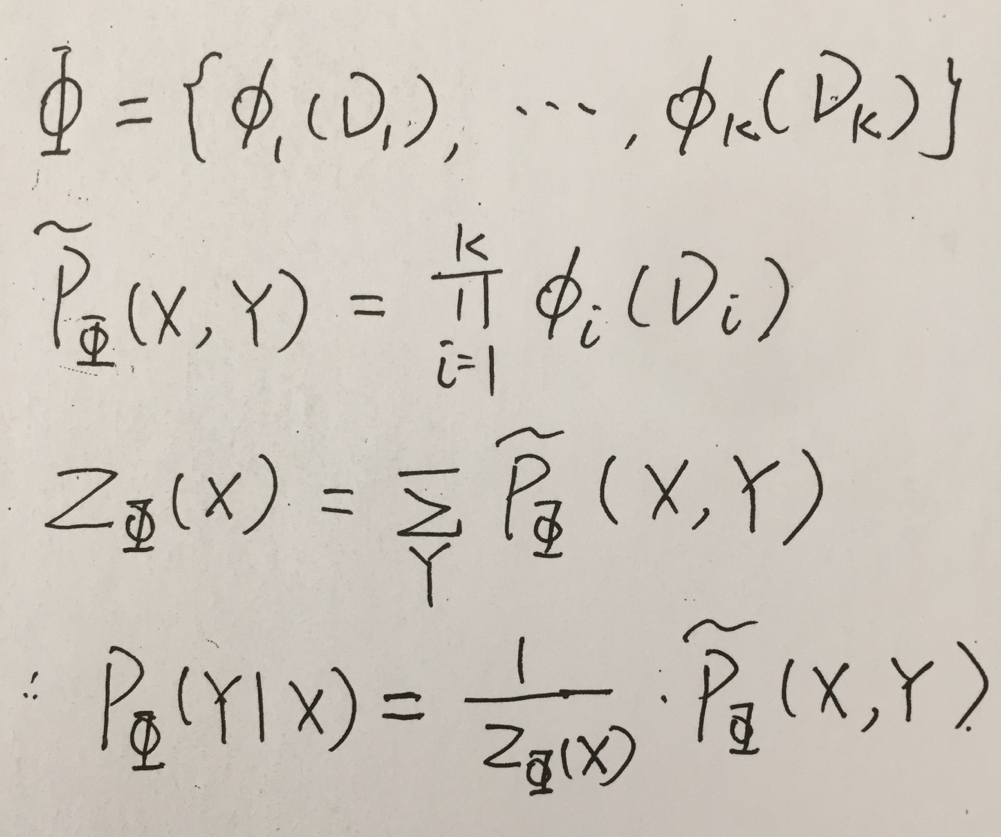
　　对于sigmoid函数，其实也是可以由条件随机场推导出来的，具体的推导过程如下：

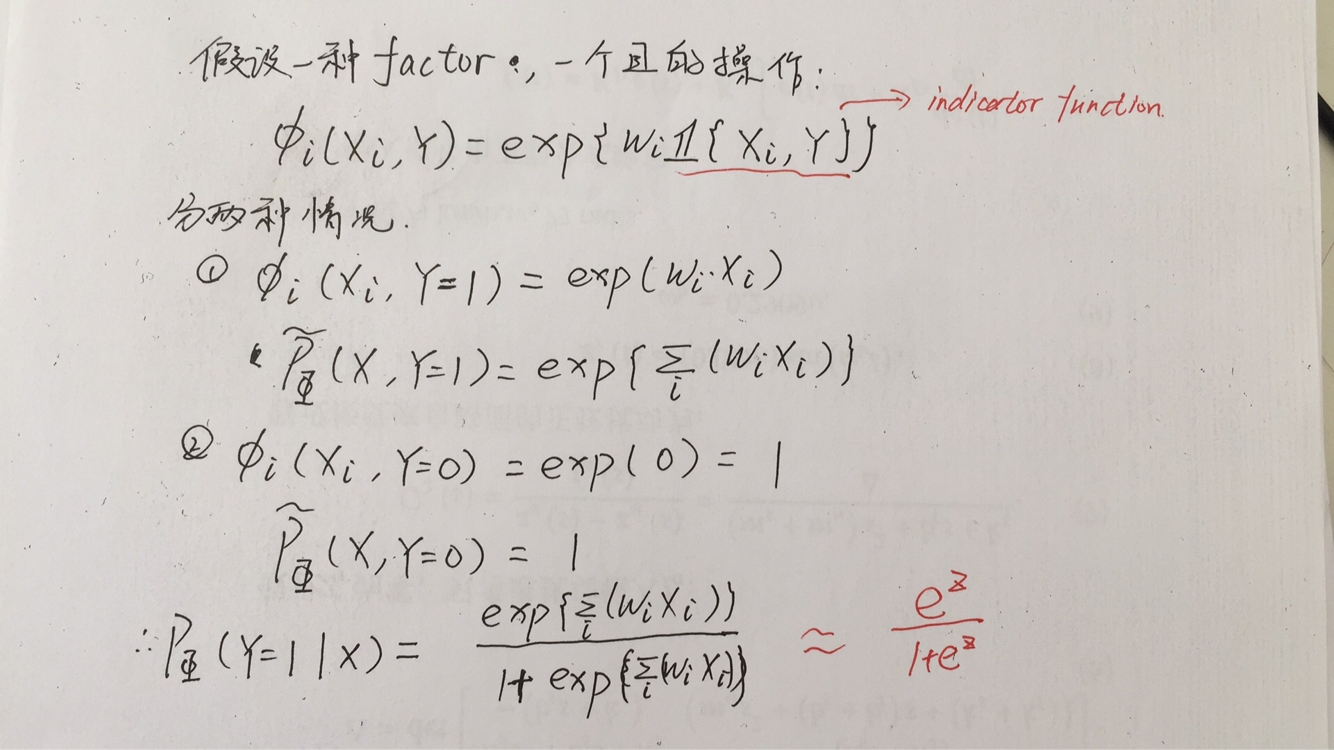
　　对于indicator function的解释详见视频：https://www.youtube.com/watch?v=V3pnr5gmJC8&t=328s

 

三、马尔科夫网络的独立性

　　如果网络 H 中的两个节点 X , Y 之间的任意一条路径，都不是通路（期间有节点已知），那么 X , Y 之间相互独立。

1、I-maps

　　马尔科夫网络中的i-map和贝叶斯网络中的定义相似

 

　　如果图G中的所有独立分布，能与P中的分布对应，那么图G就是分布P的i-map，图G中表示出的独立分布是P中独立分布的子集。图中的独立分布越多，表示这个图越稀疏，也能更好的表示出分布P中的结构，对于一个稀疏的图，有以下几点好处：

　　——有更少的参数，对于一个模型，要有适当的参数，即能够很好的表示出分布P，又能减少参数的计算量。

　　——有更多的独立分布信息，使图中分布与分布P尽可能一致。

 

1、perfect maps

　　当 I(P) = I(G) 时，G 叫做 P 的perfect map，但是存在以下几个问题

　　——perfect map可能不存在

　　——I-equivalence，一个 P 可能有很多个perfect map，每个perfect map的依赖关系还不同

perfect map不存在：

　　对于下图的情况，假设x1和x2的取值区间为{0,1}，并且概率都是0.5，做异或的操作，最终的结果分布如右边所示，由概率图中可知在给定 y 的前提下，x1 x2相互独立，但是在右边的分布中可以看出x1,x2,y三者两两独立，在这种情况之下，是不存在perfect map的。

 

I-equivalence：

　　对于两个graph G1和G2，如果I（G1）= I（G2），那么这两个图是I-equivalence，正如图中所举出的例子一样，x->y->z和x<-y->z , x<-y<-z在y已知的情况，x和z均是独立的，他们的分布是相同的，那么对于这种情况，如果不事先说明y是x的祖先等条件，是不能得出该分布是对应于哪一个概率图的。