AVL树高度平衡的二叉搜索树,任一点的平衡印章只能是+1、-1、0,从而尽量降低树的高度。
如果它有n个结点,高度可保持在O(log2n),平均搜索长度也可保持在O(log2n)。
(1)AVL树的插入
在插入一个新结点时,需要从插入位置沿通向根的路径回溯,检查各结点左右子树高度差。
发现结点的平衡因子为0,刚刚是在其较矮的子树插入新结点,从该结点到根的路径上各结点为根的子树高度不变、平衡因子不变,无需继续检查。
发现结点平衡因子|bf|=1,说明插入前是0,插入后该结点没有失去平衡。但该子树高度增加了,还需要继续往根方向检查。
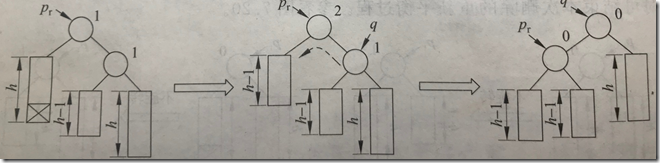
发现某一结点|bf|=2不平衡,停止回溯,做平衡化旋转。
从发生不平衡的结点起,沿刚才回溯的路径取直接下两层的结点。
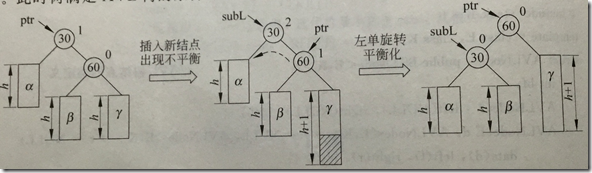
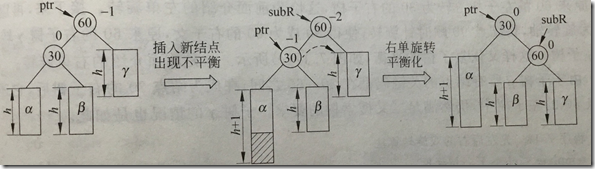
1.这三个结点位于同一条直线上,采用单旋转进行平衡化
bf=2,右子树高,查看右结点bf=1,执行左单旋转
执行后ptr和subL的bf均变为0:
bf=-2,左子树高,查看左结点bf=-1,执行右单旋转
执行后ptr和subL的bf均变为0
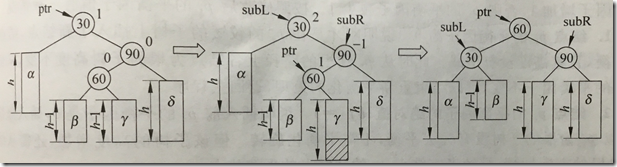
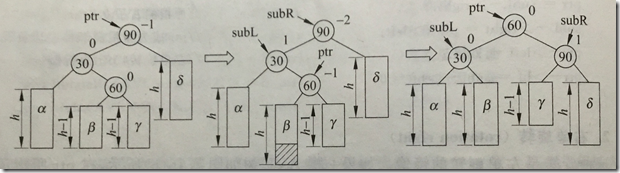
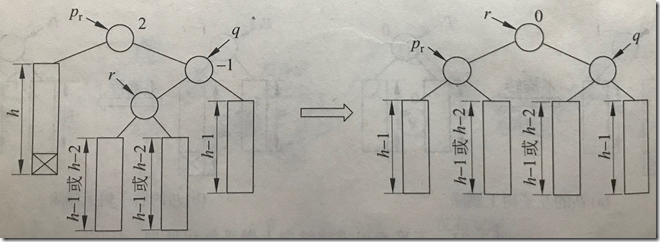
2.这三个结点位于一条折线上,采用双旋转进行平衡化
bf=2,右子树高,查看右结点bf=-1,无论ptr->bf是1还是-1,都执行先右后左双旋转
如果ptr的bf原为1,右单旋转后subR的bf改为0,先右后左双旋转,旋转后subL的bf变为-1
如果ptr的bf原为-1,右单旋转后subR的bf改为1,先右后左双旋转,旋转后subL的bf变为0
ptr的bf最终变为0
bf=-2,左子树高,查看左结点bf=1,无论ptr->bf是1还是-1,都执行先左后右双旋转
如果ptr的bf原为-1,左单旋转后subL的bf改为0,先左后右双旋转,旋转后subR的bf变为1
如果ptr的bf原为1,左单旋转后subL的bf改为-1,先左后右双旋转,旋转后subR的bf变为0
ptr的bf最终变为0
(2)AVL树的删除
1.被删结点有两个子女
寻找被删结点p在中序下的直接前驱或者直接后继q,把q的值给结点p,然后把结点q删除(q最多一个子女)
2.被删结点最多一个子女q
直接把p的父结点pr中原来指向p的指针指向q。
q是pr的左子女的话,pr的bf加1;q是pr的右子女的话,pr的bf减1。
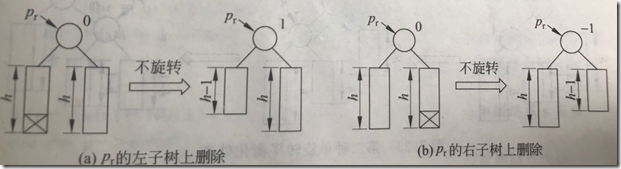
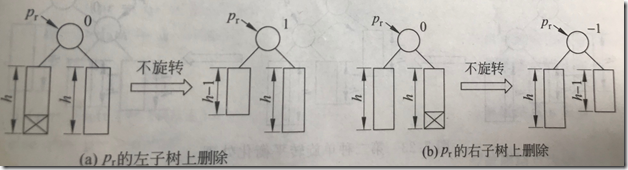
(1)pr的bf原为0,左/右子树被缩短后改为1/-1,以pr为根的子树高度未变,pr到根结点的路径上所有结点都不需要调整。
(2)pr的bf原不为0,较高的子树被缩短,bf变为0。
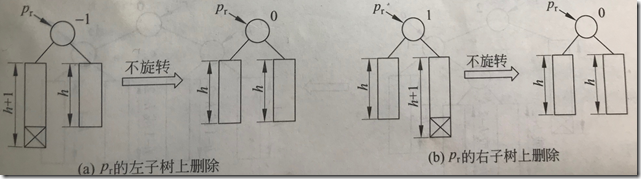
以pr为根的子树虽然平衡,但高度减少了。需要继续考察其父结点。
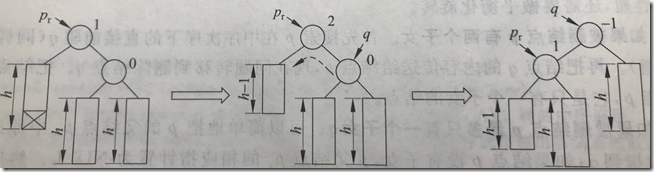
(3)pr的bf原不为0,较矮的子树又被缩短,bf变为±2。令q指向pr的较高的子树
①q->bf==0的情况:
pr的bf=2,右子树较高,右子树q的bf为0,作左单旋转
旋转后q->bf=pr->bf=0,还要把q->pf改为-1,pr->bf改为1
pr的bf=-2,左子树较高,左子树q的bf为0,作右单旋转
旋转后q->bf=pr->bf=0,还要把q->pf改为1,pr->bf改为-1
②pr->bf和q->bf正负号相同的情况:
pr的bf=2,右子树较高,右子树q的bf=1,执行左单旋转,旋转后q->bf=pr->bf=0
pr的bf=-2,左子树较高,左子树q的bf=-1,执行右单旋转,旋转后q->bf=pr->bf=0
③pr和p的bf正负号相反,执行双旋转,先绕q转一次,再绕pr转一次:
pr的bf=2,右子树较高,右子树q的bf为-1,执行先右后左双旋转
pr的bf=-2,左子树较高,左子树q的bf为1,执行先左后右双旋转
处理后子树高度减少1,继续考察其父结点。
#include <iostream> #include "stack.h" using namespace std; template <class E,class K> struct AVLNode:public BSTNode<E,K>{ int bf; //右子树高度-左子树高度 AVLNode():left(NULL),right(NULL),bf(0){} AVLNode(E d,AVLNode<E,K> *l=NULL,AVLNode<E,K> *r=NULL):data(d),left(l),right(r),bf(0){} } template <class E,class K> class AVLTree:public BST<E,K>{ public: AVLTree():root(NULL){} AVLTree(K Ref):RefValue(Ref),root(NULL){} bool Insert(E& el){return Insert(root,el);} bool Remove(K x,E& el){return Remove(root,el);} friend istream& operator>>(istream& in,AVLTree<E,K>& tree); friend ostream& operator<<(ostream& out,AVLTree<E,K>& tree); int Height()const; protected: AVLNode<E,K> *Search(K x,AVLNode<E,K>* &par)const; bool Insert(AVLNode<E,K>* &ptr,E& el); bool Remove(AVLNode<E,K>* &ptr,K x,E& el); void RotateL(AVLNode<E,K>* &ptr); void RotateR(AVLNode<E,K>* &ptr); void RotateLR(AVLNode<E,K>* &ptr); void RotateRL(AVLNode<E,K>* &ptr); int Height(AVLNode<E,K> *ptr)const; void AVLTree<E,K>::Traverse(AVLNode<E,K> *ptr,ostream& out)const; } template <class E,class K> void AVLTree<E,K>::RotateL(AVLNode<E,K>* &ptr){ //右子树比左子树高,对以ptr为根的AVL树做左单旋转,旋转后新根在ptr AVLNode<E,K> *subL=ptr; ptr=subL->right; //两个结点平衡因子均为正,需要做左单旋转 subL->right=ptr->left; ptr->left=subL; ptr->bf=subL->bf=0; } template <class E,class K> void AVLTree<E,K>::RotateR(AVLNode<E,K>* &ptr){ //左子树比右子树高,对以ptr为根的AVL树做右单旋转,旋转后新根在ptr AVLNode<E,K> *subR=ptr; ptr=subR->left; //两个结点平衡因子均为负,需要做右单旋转 subR->left=ptr->right; ptr->right=subR; ptr->bf=subR->bf=0; } template <class E,class K> void AVLTree<E,K>::RotateLR(AVLNode<E,K>* &ptr){ AVLNode<E,K> *subR=ptr,*subL=ptr->left; ptr=subL->right; subL->right=ptr->left; ptr->left=subL; if(ptr->bf<=0) subL->bf=0; //如果ptr->bf原为-1,左单旋转后subL->bf为0 else subL->bf=-1; //如果ptr->bf原为1,左单旋转后subL->bf为-1 subR->left=ptr->right; ptr->right=subR; if(ptr->bf==-1) subR->bf=1; //如果ptr->bf原为-1,先左后双旋转后subR->bf为1 else subR->bf=0; //如果ptr->bf原为1,先左后双旋转后subR->bf为0 ptr->bf=0; } template <class E,class K> void AVLTree<E,K>::RotateRL(AVLNode<E,K>* &ptr){ AVLNode<E,K> *subL=ptr,*subR=ptr->right; ptr=subR->left; subR->left=ptr->right; ptr->right=subR; if(ptr->bf>=0) subR->bf=0; else subR->bf=1; subL->right=ptr->left; ptr->left=subL; if(ptr->bf==1) subL->bf=-1; else subL->bf=0; ptr->bf=0; } template <class E,class K> bool AVLTree<E,K>::Insert(AVLNode<E,K>* &ptr,E& el){ //改变bf的步骤在旋转中做了,Insert方法中无需再改变 AVLNode<E,K> *pr=NULL,*p=ptr,*q; int d; stack<AVLNode<E,K>*> st; while(p!=NULL){ if(el==p->data) return false; pr=p; st.push(pr); if(el<p->data) p=p->left; else p=p->right; } p=new AVLNode<E,K>(el); if(p==NULL){ cerr<<"存储空间不足!"<<endl; exit(1); } if(pr==NULL){ //空树,新结点成为根结点 ptr=p; return true; } if(el<pr->data) pr->left=p; else pr->right=p; while(!st.IsEmpty()){ st.Pop(pr); if(p==pr->left) pr->bf--; //调整父结点平衡因子 else pr->bf++; //第一种情况,平衡因子为0,说明刚才在pr较矮的子树上插入新结点,结点pr处平衡且高度未变。结点pr到根的路径上所有结点为根的子树高度都未变。可以直接结束重新平衡化的处理。 if(pr->bf==0) break; //第二种情况,平衡因子绝对值为1,说明插入前平衡因子为0,插入后以pr为根的子树没有失去平衡,但仍然需要检查结点pr到根的路径上所有结点为根的子树 if(pr->bf==1 || pr->bf==-1) p=pr; //第三种情况,平衡因子绝对值为2,说明新结点在较高的子树上插入,造成了不平衡,需要做平衡化旋转 else{ d=(pr->bf<0)?-1:1; if(p->bf==d){ //两结点平衡因子同号,单旋转 if(d==-1) RotateR(pr); //pr的bf为-2,p的bf为1,右单旋转 else RotateL(pr); //pr的bf为2,p的bf为-1,左单旋转 } else{ if(d==-1) RotateLR(pr); //pr的bf为2,p的bf为-1,先右后左旋转 else RotateRL(pr); //pr的bf为-2,p的bf为-1,先左后右旋转 } break; //旋转之后以pr为根的子树高度降低,无需再向上层回溯 } } if(st.IsEmpty()) ptr=pr; //栈空,pr作为新根 else{ st.getTop(q); //栈不空,取出pr的父结点 if(q->data>pr->data) q->left=pr; else q->right=pr; } return true; } template <class E,class K> istream& operator>>(istream& in,AVLTree<E,K>& Tree){ E item; cout<<"Construct AVL tree: "; cout<<"Input Data(end with"<<Tree.RefValue<<"):"; in>>item; while(item.key!=Tree.RefValue){ Tree.Insert(item); cout<<"Input Data(end with"<<Tree.RefValue<<"):"; in>>item; } return in; } template <class E,class K> ostream& operator<<(ostream& out,const AVLTree<E,K>& Tree){ out<<"Inorder traversal of AVL tree. "; Tree.Traverse(Tree.root,out); out<<endl; return out; } template <class E,class K> void AVLTree<E,K>::Traverse(AVLNode<E,K> *ptr,ostream& out)const{ if(ptr!=NULL){ Traverse(ptr->left,out); out<<ptr->data<<''; Traverse(ptr->right,out); } } template <class E,class K> bool AVLTree<E,K>::Remove(AVLNode<E,K>* &ptr,K x,E& el){ AVLNode<E,K> *pr=NULL,*p=ptr,*q,*ppr; int d,dd=0; while(p!=NULL){ if(k==p->data.key) break; pr=p; st.Push(pr); if(k<p->data.key) p=p->left; else p=p->right; } if(p==NULL) return false; if(p->left!=NULL && p->right!=NULL){ //被删结点有两个子女 pr=p; st.Push(pr); q=p->left; //在p的左子树找p的直接前驱 while(q->right!=NULL){ pr=q; st.Push(pr); q=q->right; } p->data=q->data; p=q; //被删结点转换为q,q最多一个子女 } if(p->left!=NULL) q=p->left; //被删结点只有一个子女或者没有子女 else q=p->right; if(pr==NULL) ptr=q; //被删结点为根结点,让其子女成为新根 else{ //被删结点不是根结点 if(pr->left==p) pr->left=q; //p的父结点pr原本指向p的指针改指向q else pr->right=q; while(!st.IsEmpty()){ //重新平衡化 st.Pop(pr); //从栈中推出父结点 if(pr->right==q) pr->bf--; //调整父结点的平衡因子 else pr->bf++; if(!st.IsEmpty()){ st.getTop(ppr); //从栈中取出祖父结点 dd=(ppr->left==pr)?-1:1; //旋转后与上层链接方向 } else dd=0; //栈空,旋转后不与上层链接 if(pr->bf==1 || pr->bf==-1)//pr的平衡因子原为0,在它的左/右子树被缩短后,平衡因子变为1或者-1,以pr为根的子树高度没有改变,从pr到根结点的路径上所有结点都不需要调整 break; if(pr->bf!=0){ if(pr->bf<0){d=-1;q=pr->left;} else{d=1;q=pr->right;} if(q->bf==0){ if(d==-1){ //pr的平衡因子为-2,左子树q的平衡因子为0,执行右单旋转 RotateR(pr); pr->bf=1; pr->left->bf=-1; } else{ //pr的平衡因子为2,右子树q的平衡因子为0,执行左单旋转 RotateL(pr); pr->bf=-1; pr->right->bf=1; } break; } if(q->bf==d){ //q和pr的平衡因子正负号相同,执行一个单旋转来恢复平衡 if(d==-1) RotateR(pr); //pr平衡因子为-2,p平衡因子为-1,右单旋转 else RotateL(pr); //pr平衡因子为2,p平衡因子为1,左单旋转 } else{ //q和pr的平衡因子正负号相反,执行一个双旋转来恢复平衡 if(d==-1) RotateLR(pr); //pr的bf=-2,左子树较高,左子树p的bf为1,执行先左后右双旋转 else RotateRL(pr); //pr的bf=2,右子树较高,右子树p的bf为-1,执行先右后左双旋转 } if(dd==-1) ppr->left=pr; else if(dd==1) ppr->right=pr; //旋转后新根与上层链接 } q=pr; //pr的平衡因子变为0(较高的子树被缩短了),此时以pr为根的树平衡但高度减少1,需要继续考察pr父结点的平衡状态 } if(st.IsEmpty()) ptr=pr; //调整到树的根结点 } delete p; return true; }