混合整数线性规划，图的最大流，图的匹配，求解

求解软件有，

matlab，lingo，商用软件

GLPK，GNU LP Kit，开源，ansi C

介绍图的匹配，matching

https://www.tutorialspoint.com/graph_theory/graph_theory_matchings.htm

最大流问题，有许多图的基础知识

https://blog.csdn.net/qq_39557517/article/details/81945749

介绍如何使用GLPK

https://www-sop.inria.fr/members/Frederic.Giroire/teaching/ubinet/pdfs/exercises-solvers.pdf

线性规划基本介绍：https://www.cs.cmu.edu/~ckingsf/bioinfo-lectures/linearp.pdf

线性规划三种求解方法：

Simplex method，单纯形法，古老的方法，虽然不是多项式时间算法，但实际计算很快；

Ellipsoid method，椭球方法，1970s提出，虽然是多项式时间算法，但实际效果差，很少用；

Interior point method，多项式时间算法，实用。

最大二分匹配，maximum bipartite matching

最大流问题求解：

下面这个例子简单一些：

http://www.cs.cornell.edu/~tomf/pyglpk/ex_maxflow.html

与这个图类似：

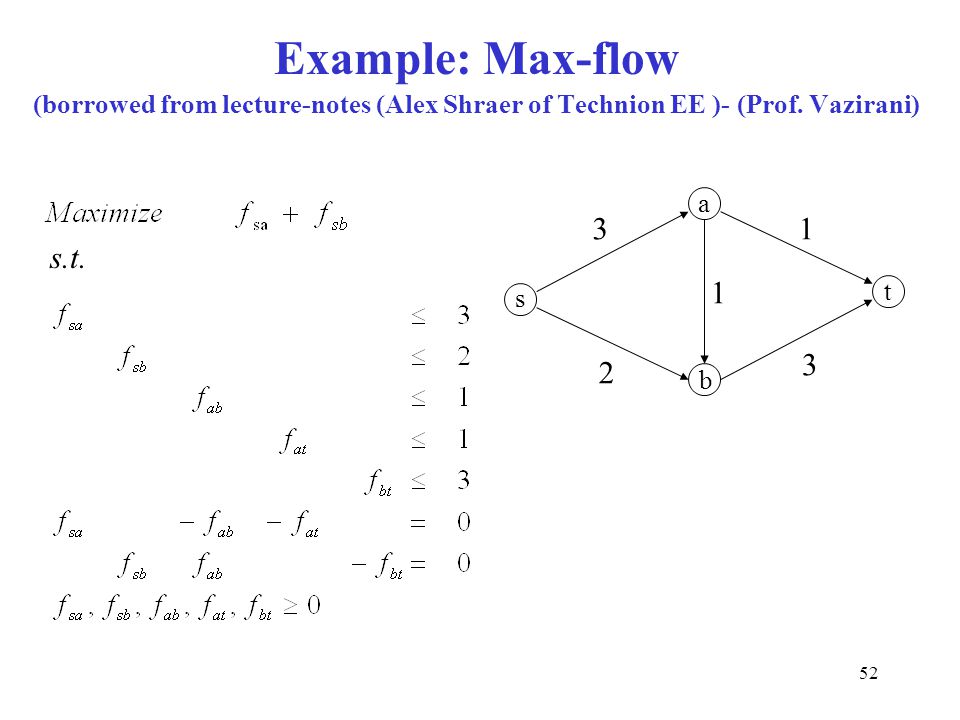
对应的matlab线性规划代码如下，有一点需要注意PPT的目标函数是max，matlab目标函数是min：

clc;clear;
A = [  1,  0,  0,  0,  0;
       0,  1,  0,  0,  0;
       0,  0,  1,  0,  0;
       0,  0,  0,  1,  0;
       0,  0,  0,  0,  1
    ];
b = [4;1;2.5;1;4];
Aeq=[  1,  0, -1, -1,  0;
       0,  1,  1,  0, -1
    ];
beq = [0;0];

f = [-1,-1,0,0,0];

x = linprog(f,A,b,Aeq,beq)

输出结果如下，最大流为4.5：

Optimization terminated.

x =

    3.5000
    1.0000
    2.5000
    1.0000
    3.5000

下面这篇很好的介绍了如何将最大流问题整理成一个线性规划问题，使用了PyGLPK 。

http://www.mathcs.emory.edu/~cheung/Courses/323/Syllabus/NetFlow/max-flow-lp.html

对应的matlab线性规划代码如下，需要使用整数线性规划：

clc;clear;
    %x01,x02,x03,x14,x15,x24,x25,x26,x35,x47,x57,x67
Aeq=[  1,  0,  0, -1, -1,  0,  0,  0,  0,  0,  0,  0;
       0,  1,  0,  0,  0, -1, -1, -1,  0,  0,  0,  0;
       0,  0,  1,  0,  0,  0,  0,  0, -1,  0,  0,  0;
       0,  0,  0,  1,  0,  1,  0,  0,  0, -1,  0,  0;
       0,  0,  0,  0,  1,  0,  1,  0,  1,  0, -1,  0;
       0,  0,  0,  0,  0,  0,  0,  1,  0,  0,  0, -1
    ];
beq = [0;0;0;0;0;0];
    %x01,x02,x03,x14,x15,x24,x25,x26,x35,x47,x57,x67
A = [  1,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0;
       0,  1,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0;
       0,  0,  1,  0,  0,  0,  0,  0,  0,  0,  0,  0;
       0,  0,  0,  1,  0,  0,  0,  0,  0,  0,  0,  0;
       0,  0,  0,  0,  1,  0,  0,  0,  0,  0,  0,  0;
       0,  0,  0,  0,  0,  1,  0,  0,  0,  0,  0,  0;
       0,  0,  0,  0,  0,  0,  1,  0,  0,  0,  0,  0;
       0,  0,  0,  0,  0,  0,  0,  1,  0,  0,  0,  0;
       0,  0,  0,  0,  0,  0,  0,  0,  1,  0,  0,  0;
       0,  0,  0,  0,  0,  0,  0,  0,  0,  1,  0,  0;
       0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  1,  0;
       0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  1
    ];
b = [3;2;2;5;1;1;3;1;1;4;2;4];

f = [-1,-1,-1,0,0,0,0,0,0,0,0,0];

intcon = [1:12];
x = intlinprog(f,intcon,A,b,Aeq,beq)

输出结果如下，最大流为6：

LP:                Optimal objective value is -6.000000.                                            


Optimal solution found.

Intlinprog stopped at the root node because the
objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are
integer within tolerance, options.IntegerTolerance = 1e-05 (the default
value).


x =

     3
     2
     1
     3
     0
     1
     1
     0
     1
     4
     2
     0