Description
卖方:这件商品14元 买方:给你20元 卖方:不好意思,我的零钱不够 买方:好吧,这是15元,剩的当小费
当到一个地方旅游时,如果你买东西的地方不支持信用,带零钱还是非常有用的。特别是有时候卖方没有零钱,如果你没有刚好的钱,你需要支付比卖价多一点。
当然你想付尽量少的钱(至少是商品价值的钱)。并且,当支付最少钱的时候,也最好是支付的硬币的数量最少。
Input
第一行包含一个整数表示测试数据的组数。每组测试数据每一行包含一个整数,表示你需要付的钱数,钱数不超过10000元。接下来包含一个整数n,表示你所拥有的钱的数量,n最多是100,接下来的n行每行一个整数,表示你有的每个硬币的面值,注意钱的面值可以是任意的,不和我们现在用的面值一样,钱的面值不超过10000元。
Output
对每组测试数据,在一行上输出两个整数:需要支付的钱数和数量。
Sample Input
1
1400
3
500
1000
2000
Sample Output
1500 2
动态规划问题,当成0-1背包处理,也可以当成多重背包。
这里当成0-1背包处理即可,物品最多就100种,每种取或不取
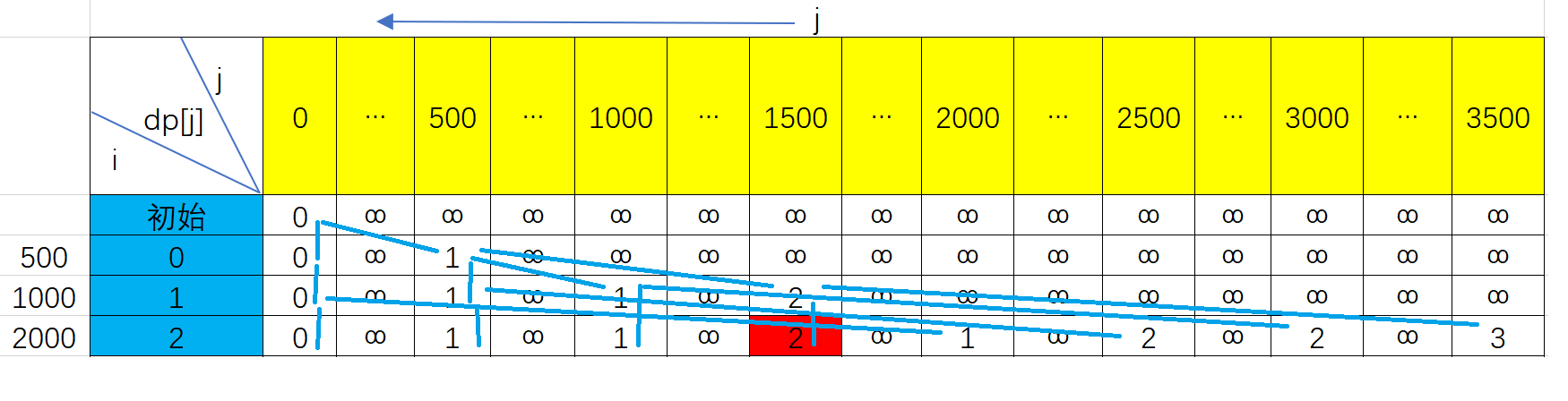
dp[j]是价值j需要dp[j]张钱
dp[j]先初始化正无穷,表示价值j的没有钱可以凑出j
dp[0] = 0,表示0元需要0张钱。
递推公式:
$$ dp[j] = egin{cases} min(dp[j - num[i]] + 1, dp[j]) & i = 1 -> n, j = 20000 -> num[i] end{cases} $$
也可以用二维数组,只不过开辟的空间大
dp[i][j]表示前i张面值可以组成价值j的最少张数
dp[i][j]全部初始化正无穷,dp[0][0] = 0
递推公式:
$$ dp[i][j] = egin{cases} min(dp[i - 1][j - num[i]] + 1, dp[i - 1][j]) & j >= num[i] \ dp[i - 1][j] & 0 <= j < num[i] \ end{cases} $$
最后找dp[j],从j = 输入的价钱,开始找满足条件且价钱最小的
AC代码:
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int dp[20001];
int main()
{
ios::sync_with_stdio(false); // 避免cout, cin导致TLE
int n;
cin >> n; // n组测试数据
while (n--)
{
memset(dp, 0x7f, sizeof(dp)); // dp全部置正无穷
dp[0] = 0; // 第一个元素置零
int price, money_nums; // price是价钱, money_nums是钱的张数
cin >> price >> money_nums;
int money[100]; // 钱面值数组
for (int i = 0; i < money_nums; i++)
cin >> money[i];
for (int i = 0; i < money_nums; i++)
for (int j = 20000; j >= money[i]; j--) // 逆序进行
dp[j] = min(dp[j], dp[j - money[i]] + 1); // 递推公式
for (int i = price; i <= 20000; i++)
{
if (dp[i] <= 100) // 找到第一个满足钱数最小的, 并且张数小于100, dp[i]已经是最优的
{
cout << i << ' ' << dp[i] << endl; // 输出结果
break;
}
}
}
return 0;
}
一开始数组开10000,提交通过了
后来发现,有些测试数据应该通过不了
比如:
1
10000
2
9999
9999
19998 2
之前的代码会什么都不输出,
把数组开成20000就行了。
之前没考虑这种特殊情况,碰巧通过了