划分问题(Java 动态规划)

Description

给定一个正整数的集合A={a1,a2,….,an},是否可以将其分割成两个子集合，使两个子集合的数加起来的和相等。例A = { 1, 3, 8, 4, 10} 可以分割：{1, 8, 4} 及 {3, 10}

Input

第一行集合元素个数n　　n <=300 第二行n个整数

Output

如果能划分成两个集合，输出任意一个子集，否则输出“no”

Sample Input

5
1 3 8 4 10

Sample Output

3 10

一开始t[i][j]都为false

递推公式：

$$ t[i][j] = egin{cases} true & i = 1, j = 0 \ true & i = 1, j = num[1] \ t[i - 1][j] || t[i - 1][j - num[i]] & i > 1, j <= sum / 2 end{cases} $$

j - num[i]大于等于0的时候才行，下标为负可能会有问题

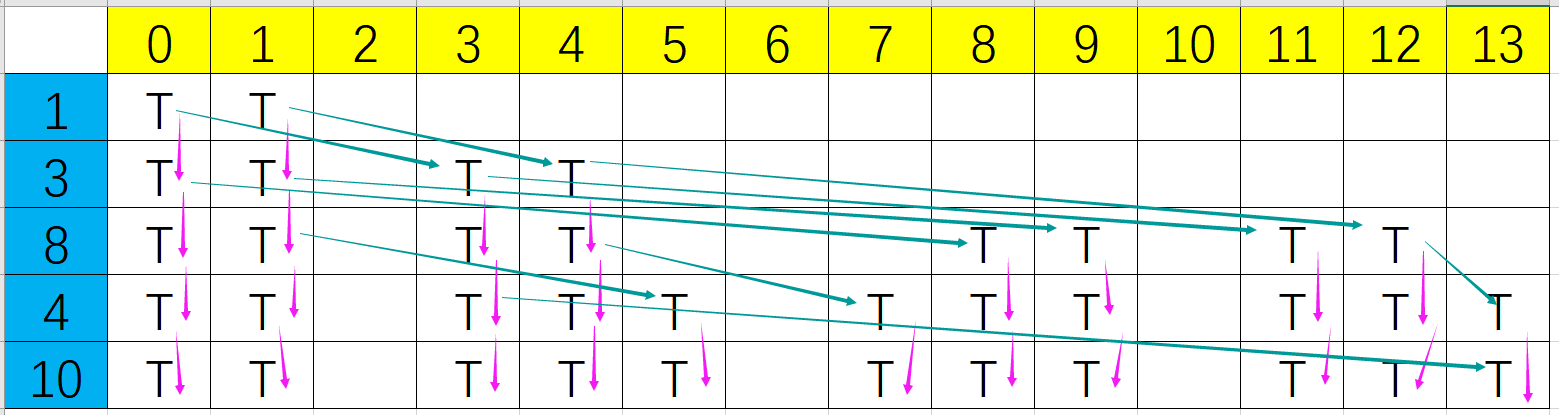
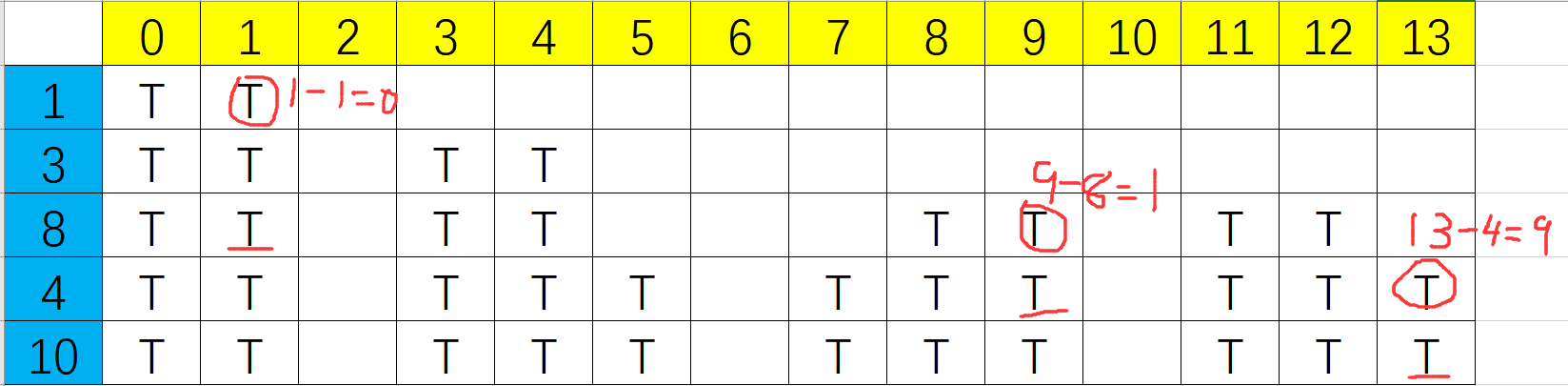
找出子集之一的方法

AC代码:

import java.util.Scanner;
 
public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int num[] = new int[n + 1];
        int sum = 0, max = 0;
 
        for (int i = 1; i <= n; i++) {
            num[i] = sc.nextInt();
            sum += num[i];
            max = Math.max(max, num[i]);		// 找输入的数中最大的
        }
        sc.close();
 
        if (sum % 2 != 0 || max > (sum / 2) || n == 0) { 
            // 如果所有数的和不为偶数或最大的数大于和的一半或n=0直接输出no, 并且return
            System.out.println("no");
            return;
        }
 
        sum /= 2;	// 和除2
        boolean dp[][] = new boolean[n + 1][sum + 1];
        dp[1][0] = true;		// 初始化dp数组
        dp[1][num[1]] = true;	// 初始化dp数组
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j <= sum; j++) {
                if (dp[i - 1][j] || ((j - num[i] >= 0) && dp[i - 1][j - num[i]]))
                    dp[i][j] = true;	// 满足递推公式的标记上
            }
        }
 
        if (dp[n][sum]) {	// 满足可划分, 输出其中一个子集
            int j = sum;
            while (j > 0) {
                for (int i = n; i >= 1; i--) {
                    if (dp[i][j] && !dp[i - 1][j]) {
                        j -= num[i];
                        System.out.printf("%d%c", num[i], j == 0 ? '
' : ' ');
                        if (j == 0)		// 找完结束退出
                            break;
                    }
                }
            }
        }
        else
            System.out.println("no");	// 不满足可划分, 输出no
    }
}