1.前向分布算法
其算法的思想是,因为学习的是加法模型,如果能够从前往后,每一步只学习一个基函数及其系数,逐步逼近优化目标函数,那么就可以简化优化的复杂度。

2.负梯度拟合
对于一般的回归树,采用平方误差损失函数,这时根据前向分布每次只需要达到最优化,就能保证整体上的优化。由于平方误差的特殊性,可以推导出每次只需要拟合残差(真实值-预测值)。
为什么采用损失函数的负梯度?
L(y,f(x))中将f(x)看成一个参数,为了使L损失函数最小,采用梯度下降的方法即:
f(x)_m=f(x)_m-1-(dL/df(x))//与一般的梯度下降法相同
而f(x)_m=f(x)_m-1+T(x;Q)//Q为前向分布法每次得到这棵树的参数,T(x;Q)为训练的新树
所以有f(x)_m-1+T(x;Q)=f(x)_m-1-(dL/df(x))
所以有T(x;Q)=-(dL/df(x))
左边为预测值,右边为真实值,所以整个过程就变成了每次拟合损失函数的负梯度的值。
3.损失函数
这里我们再对常用的GBDT损失函数做一个总结。
1.对于分类算法,其损失函数一般有对数损失函数和指数损失函数两种:
(1)如果是指数损失函数,则损失函数表达式为

其负梯度计算和叶子节点的最佳残差拟合参见Adaboost原理篇。
(2)如果是对数损失函数,分为二元分类和多元分类两种,
对于二元分类
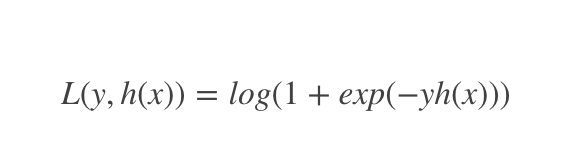
2.对于回归算法,常用损失函数有如下4种:
(1)均方差,这个是最常见的回归损失函数了

(2)绝对损失,这个损失函数也很常见

对应负梯度误差为:
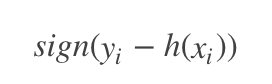
(3)Huber损失,它是均方差和绝对损失的折衷产物,对于远离中心的异常点,采用绝对损失,而中心附近的点采用均方差。这个界限一般用分位数点度量。
(4)分位数损失。它对应的是分位数回归的损失函数。
4.回归
输入:训练样本 D={(x1,y1),(x2,y2),⋯,(xm,ym)}D={(x1,y1),(x2,y2),⋯,(xm,ym)},最大迭代次数(基学习器数量) TT,损失函数 LL
输出:强学习器 H(x)H(x)
算法流程
Step1:初始化基学习器
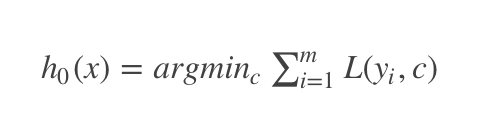
Step2:当迭代次数 t=1,2,⋯,Tt=1,2,⋯,T
(1)计算 t 次迭代的负梯度
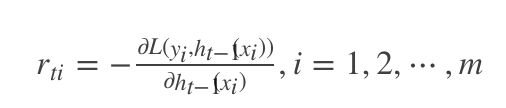
(2)利用 (xi,rti)(i=1,2,⋯,m)(xi,rti)(i=1,2,⋯,m),拟合第 t 棵CART回归树,其对应的叶子结点区域为 Rtj,j=1,2,⋯,JRtj,j=1,2,⋯,J。 其中 JJ 为回归树的叶子结点的个数
(3)对叶子结点区域 j=1,2,⋯,Jj=1,2,⋯,J,计算最佳拟合值
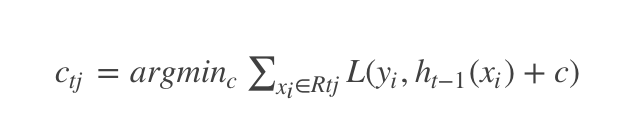
(4)更新强学习器
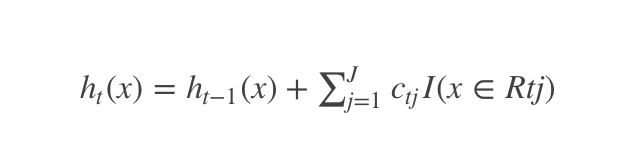
Step3:得到强学习器
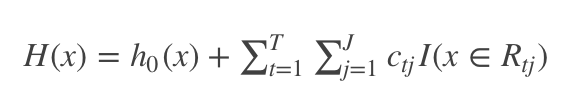
5.二分类
对于二元GBDT,如果用类似于逻辑回归的对数似然损失函数,则损失函数为:
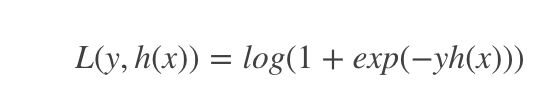
其中,y∈{−1,+1}y∈{−1,+1}。此时的负梯度误差是

对于生成的决策树,我们各个叶子节点的最佳残差拟合值为
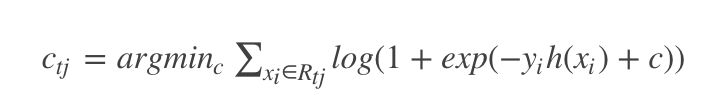
由于上式比较难优化,我们一般使用近似值代替

除了负梯度计算和叶子节点的最佳残差拟合的线性搜索,二元GBDT分类和GBDT回归算法过程相同。
6.正则化
和Adaboost一样,我们也需要对GBDT进行正则化,防止过拟合。GBDT的正则化主要有三种方式。
(1)第一种是和Adaboost类似的正则化项,即步长(learning rate)。定义为ν,对于前面的弱学习器的迭代
Ht(x)=Ht−1(x)+ht(x)Ht(x)=Ht−1(x)+ht(x)
如果我们加上了正则化项,则有
Ht(x)=Ht−1(x)+αht(x),0<α≤1Ht(x)=Ht−1(x)+αht(x),0<α≤1
对于同样的训练集学习效果,较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
(2)第二种正则化的方式是通过子采样比例(subsample)。取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。
使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。
(3)第三种是对于弱学习器即CART回归树进行正则化剪枝。在决策树原理篇里我们已经讲过,这里就不重复了。
7.优缺点
GBDT主要的优点有:
(1)可以灵活处理各种类型的数据,包括连续值和离散值。
(2)在相对少的调参时间情况下,预测的准备率也可以比较高。这个是相对SVM来说的。
(3)使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
GBDT的主要缺点有:
(1)由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
8.sklearn参数

loss:损失函数度量,有对数似然损失deviance和指数损失函数exponential两种,默认是deviance,即对数似然损失,如果使用指数损失函数,则相当于Adaboost模型。
criterion: 样本集的切分策略,决策树中也有这个参数,但是两个参数值不一样,这里的参数值主要有friedman_mse、mse和mae3个,分别对应friedman最小平方误差、最小平方误差和平均绝对值误差,friedman最小平方误差是最小平方误差的近似。
subsample:采样比例,这里的采样和bagging的采样不是一个概念,这里的采样是指选取多少比例的数据集利用决策树基模型去boosting,默认是1.0,即在全量数据集上利用决策树去boosting。
warm_start:“暖启动”,默认值是False,即关闭状态,如果打开则表示,使用先前调试好的模型,在该模型的基础上继续boosting,如果关闭,则表示在样本集上从新训练一个新的基模型,且在该模型的基础上进行boosting。
属性/对象
feature_importance_:特征重要性。
oob_improvement_:每一次迭代对应的loss提升量。oob_improvement_[0]表示第一次提升对应的loss提升量。
train_score_:表示在样本集上每次迭代以后的对应的损失函数值。
loss_:损失函数。
estimators_:基分类器个数。
方法
apply(X):将训练好的模型应用在数据集X上,并返回数据集X对应的叶指数。
decision_function(X):返回决策函数值(比如svm中的决策距离)
fit(X,Y):在数据集(X,Y)上训练模型。
get_parms():获取模型参数
predict(X):预测数据集X的结果。
predict_log_proba(X):预测数据集X的对数概率。
predict_proba(X):预测数据集X的概率值。
score(X,Y):输出数据集(X,Y)在模型上的准确率。
staged_decision_function(X):返回每个基分类器的决策函数值
staged_predict(X):返回每个基分类器的预测数据集X的结果。
staged_predict_proba(X):返回每个基分类器的预测数据集X的概率结果。
9.应用场景
回归,分类
参考资料:http://www.cnblogs.com/pinard/p/6140514.html