激活函数就是非线性函数,常用于非线性模型,特别是神经网络;
非线性函数用于构建非线性决策边界,多个非线性函数的组合能够构建复杂的决策面;
本文旨在总结这些函数,并进行对比分析
阶跃函数
最早的激活函数,图如下
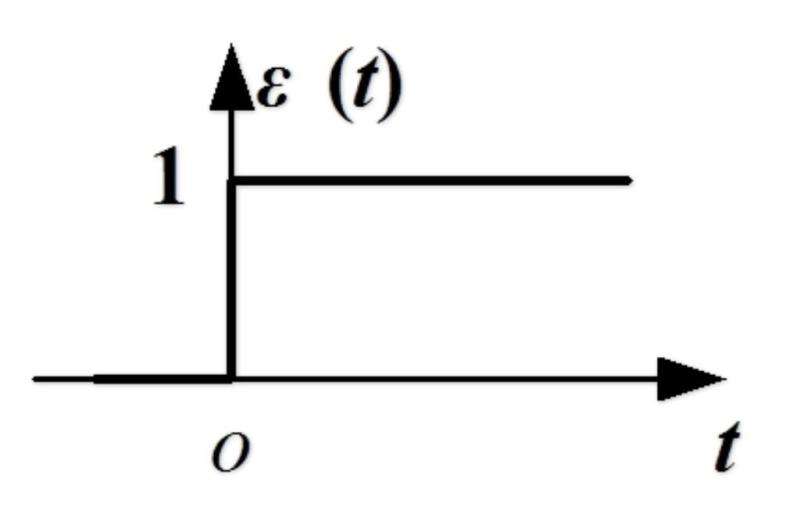
缺点:不连续,且局部导数为 0,无法反向传播
它只用在 感知器 上
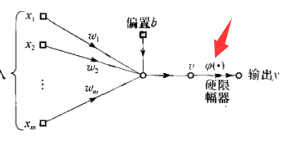
sigmoid
它是用来替代 阶跃函数的,图如下,有没有发现长得很像
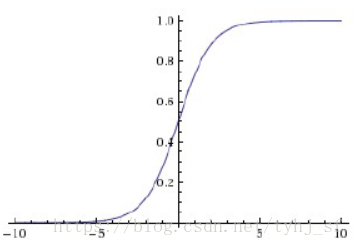
计算公式如下
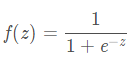
优点:
1. 有个很好的性质,即 f'(x) = f(x)[1-f(x)],这样求导就很方便了,无需额外计算
2. 把信号压缩在 01 之间,使得信号值连续,且数值变小
缺点:
sigmoid 在深度学习中几乎被弃用,最大的问题是容易梯度消失,因为
a) sigmoid 在两侧梯度趋于 0,且在大部分 x 上,其对应的梯度趋近于 0,只有中间一小部分,梯度明显,但是你敢指望 x 取到这么小个区间?
b)sigmoid 梯度最大为 x=0 时,此时梯度值为 f(0)[1-f(0)] = 0.25,最大才 0.25,岂不是很容易消失
下图为 sigmoid 导数图
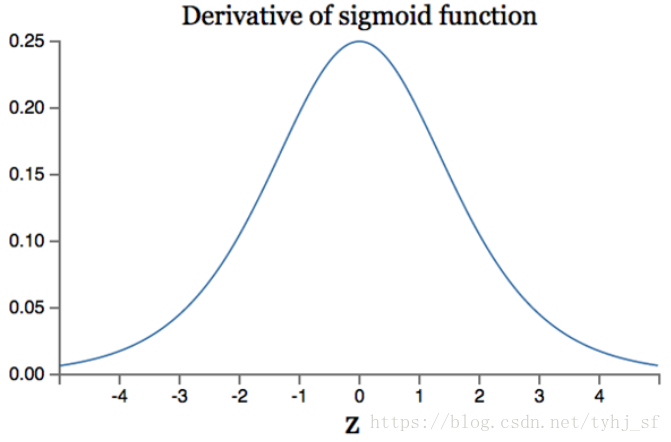
最大 0.25,abs(x)>4,梯度几乎为 0 了
还有一些不太致命的缺点:
1. 冥函数,计算耗时,增加训练时间
2. 输出不是 0 均值,即 zero-centered,若 x>0,则 f(x)>0,梯度也大于 0,两个 大于0 相乘 仍然大于0,这样 w 就一直往一个方向调整,收敛缓慢;
当然 batch 可以缓解这个问题
3. 在梯度较大的区域,也就是中间那块,模型趋于线性
tanh
双曲正切,图如下(左)
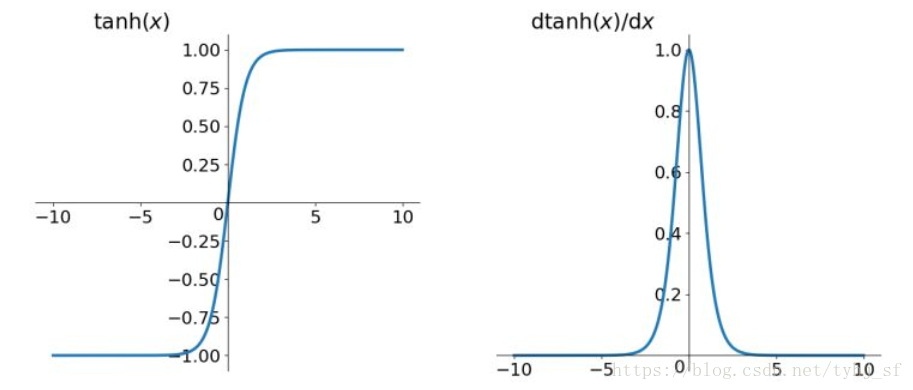
表达式
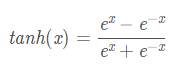
优点:
1. 解决了 sigmoid 的 非0均值问题
2. 它的求导也很方便,f'(x) = 1-f2(x)
缺点:同 sigmoid 一样,梯度消失
ReLu
在深度学习中应用最广的激活函数,图如下
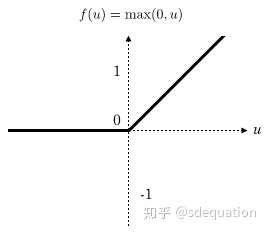
他本质是个分段线性模型,多个 relu 可以构建非线性决策面
优点:
1. 避免梯度消失
2. 求导极其方便,只需判断 是否大于0,计算速度快
3. 梯度恒为1,收敛速度快 【sigmoid 梯度最大才 0.25】
4. ReLU关闭了右边,从而会使得很多的隐层输出为0,即网络变得稀疏,起到了类似L1的正则化作用,可以在一定程度上缓解过拟合。
缺点:
1. relu 的输出也不是 zero-centered
2. Dead Relu Problem,指的是某些神经元永远不被激活,导致相应的参数永远不被更新, 导致这种情况的原因大致有两种
a) 初始化参数不当,比较少见
b) learning rate 设置过大,导致参数更新过快,不幸陷入这种状态
解决方法是可以采用 Xavier 初始化方法,以及避免将 learning rate 设置太大或使用 adagrad 等自动调节 learning rate 的算法
目前在深度学习中是最常用的激活函数
Leaky Relu
与 relu 很相似,relu 的右边是 0,leaky relu 的右边避免了 0 的出现,向下偏移了一个很小的角度,使得梯度和输出均不为 0, 图如下

表达式 f(x)=max(αx,x) α 是小于 1 的正数
优点:
一定程度上避免了 relu 的问题
参考资料:
https://blog.csdn.net/tyhj_sf/article/details/79932893
https://blog.csdn.net/God_68/article/details/85262255