jQuery火箭图标返回顶部代码

%%%lkx大佬暴力直逼AK的边缘

这qbxt对知识产权还挺重视的哈

T1：Fiborial

【问题描述】

已知：

　　当n<=1时f[n]=1;

　　当n>= 2时f[n]=n*f[n-1][n-2];

求f[n]的不同因子的个数。

【输入格式】

输入数据仅包含一个整数n

【输出格式】

输出一个整数，代表f[n]的不同因子的个数对10^9+7取模得到的结果。

【样例输入 1】

　　3

【样例输出 1】

　　4

【样例输入 2】

　　763

【样例输出 2】

　　973844299

【数据规模和约定】

对于20%的数据,n<=10;

对于40%的数据,n<=100;

对于70%的数据,n<= 500000;

对于100%的数据,n<=5000000;

Solution:

真的不想用MarkDown了（昨天一下午写了一篇解题报告有阴影了）

f[0]=1;

f[1]=1;

f[2]=2*1*1;

f[3]=3^1*2^1*1^2;

f[4]=4^1*3^1*2^2*1^3;

f[5]=5^1*4^1*3^2*2^3*1^5;

观察指数

1 1 2 3 5 8 

哦，他简直像极了那啥

对！斐波那契数列

（不用MarkDown真的好丑啊）

那么将n质因数分解，线性筛素数同时用一个m数组记录一个数i的最大的质因数，那么一个数i就可以通过不断地除上这个m的第i项得到因数分解。

分解过后，每一个质因子加上当前因子的指数。

Code：

#include <cstdio>
#include <cstdlib>
typedef long long ll;
const int N = (int)5e6;
const int S = (int)1e6;
const int mod = (int)1e9 + 7;
int f[N + 1], n, p[S + 1], cnt = 0, m[N + 1], c[N + 1];
bool v[N + 1];
inline int add(int a, int b) {
    int r = a + b;
    return r >= mod ? r - mod : r;
}
int main() {
//    freopen("fiborial.in", "r", stdin);
//    freopen("fiborial.out", "w", stdout);
    scanf("%d", &n);
    f[0] = f[1] = 1;
    for (int i = 2; i <= n; ++i) f[i] = add(f[i - 1], f[i - 2]);
    for (int i = 2; i <= n; ++i) {
        if (!v[i]) p[cnt++] = i, m[i] = i;
        for (int j = 0, tmp; j < cnt && (tmp = i * p[j]) <= n; ++j) {
            v[tmp] = true, m[tmp] = p[j];
            if (!(i % p[j])) break;
        }
    }
    for (int i = 2; i <= n; ++i)
        for (int x = i; x != 1; x /= m[x])
            c[m[x]] = add(c[m[x]], f[n - i]);
    int ans = 1;
    for (int i = 0; i < cnt; ++i)
        ans = (ll)ans * (c[p[i]] + 1) % mod;
    printf("%d
", ans);
    
    return 0;
}

取模运算比较慢，孙土蛋这个add函数极度巧妙的解决了介个问题。

T2：二叉树

【问题描述】

我们按照如下方式给二叉树进行编号：
1. 空二叉树的编号为 0；
2. 只有一个节点的二叉树的编号为 1；
3. 每棵二叉树有唯一的编号，任意两个形态不同的二叉树的编号不同；
4. 有N + 1个节点的二叉树的编号一定比N个节点的二叉树的编号大；
5. 如果两棵二叉树 A 和 B 的节点个数相同， 那么当以下两条规则满足至少
一条时，A 的编号比 B 的编号小：
 A 的左子树编号比 B 的左子树编号小；
 A 的左子树编号和 B 的左子树编号相同， 且 A 的右子树编号比 B 的
右子树编号小；
6. 在满足上述所有条件的前提下，所有二叉树的编号应当尽可能小
下图展示了部分二叉树的编号：

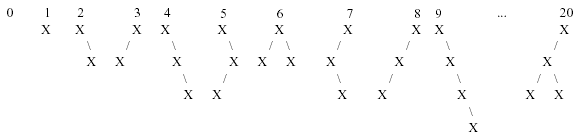
请你求出编号为N的二叉树的形态

【输入格式】

输入数据的第一行包含一个整数T，代表测试数据的组数

接下来T行，每行包含一个整数N

【输出格式】

对于每组数据，按照如下格式输出一行字符串：
对于一棵子树，如果她没有孩子，输出 X；
对于一棵有左右儿子的子树，输出(L)X(R)，其中 L 和 R 分别代表左右
儿子对应的字符串；如果左儿子为空，那么输出 X(R)；如果右儿子为
空，那么输出(L)X。

【样例输入】

3

1

20

31117532

【样例输出】

X
((X)X(X))X
(X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)

【数据规模和约定】

对于10%的数据,T=1,n=10;

对于30%的数据,T<=100,n<=1000;

对于100%的数据,T<=4000,n<=500000000;

Solutin：

找规律然后递归我不会

Code：

#include <cstdio>
#include <cstdlib>
const int N = 18;
int T, n, f[N + 1];
void build(int n, int x) {
    for (int i = 0; i < n; ++i)
        if (f[i] * f[n - i - 1] >= x) {
            if (i) {
                printf("(");
                build(i, (x - 1) / f[n - i - 1] + 1);
                printf(")");
            }
            printf("X");
            if (n - i - 1) {
                printf("(");
                build(n - i - 1, (x - 1) % f[n - i - 1] + 1);
                printf(")");
            }
            break;
        } else x -= f[i] * f[n - i - 1];
}
int main() {
//    freopen("bintree.in", "r", stdin);
//    freopen("bintree.out", "w", stdout);
    
    f[0] = 1;
    for (int i = 1; i <= N; ++i) {
        f[i] = 0;
        for (int j = 0; j < i; ++j)
            f[i] += f[j] * f[i - j - 1];
    }
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        for (int i = 1; i <= N; ++i) {
            if (f[i] >= n) {
                build(i, n);
                printf("
");
                break;
            } else n -= f[i];
        }
    }
    fclose(stdin);
    fclose(stdout);
    return 0;
}

T3:主序列

【问题描述】

有一个主序列，以及另外m个序列。请你判断这些序列是否是主序列删除若
干个数字之后得到的。

【输入格式】

输入的第一行包含一个整数n，代表主序列的长度。接下来一行包含n个空
格分隔的整数，代表主序列。
第三行包含一个整数m，代表需要判断的序列个数。每个序列用两行描述，
第一行给出其长度l[i]，第二行包含l[i] 个空格分隔的整数，代表这个序列。

【输出格式】

对于每个需要判断的序列，输出一行 Yes 或者 No，代表序列是否是由主序
列删除若干个数字后得到的。

【样例输入】

7
1 5 4 5 7 8 6
4
5
1 5 5 8 6
3
2 2 2
3
5 7 8
4
1 5 7 4
【样例输出】

Yes
No
Yes
No
【数据规模和约定】

30%的数据，n,m ≤ 1000。
对于100%的数据，n,m,∑l[i] ≤ 1000000，1 ≤序列元素≤ 1000000。

Solution:

考场上我打了个暴力期望得分30实际得分20,我个菜鸡那么简单的暴力我还打了一个小时死活调不出来

关于这题的正解

我正在努力研究.......

Code:

#include <cstdio>
#include <cstdlib>
const int N = (int)1e6;
// const int SIZE = (int)24e6;
struct node {
    int p, s, next;
} q[N + 1];
int s[N + 1], p[N + 1], st[N + 1], len[N + 1], h[N + 1], cnt = 0;
int n, m;
bool v[N + 1];
// char inbuf[SIZE], *ip = inbuf;
// inline int read() {
//     int ret = 0;
//     while (*ip > '9' || *ip < '0') ++ip;
//     while (*ip >= '0' && *ip <= '9') ret = ret * 10 + *(ip++) - '0';
//     return ret;
// }
inline void addnode(int x, int s, int p) {
    q[++cnt].s = s, q[cnt].p = p;
    q[cnt].next = h[x];
    h[x] = cnt;
}
int main() {
    freopen("seq.in", "r", stdin);
    freopen("seq.out", "w", stdout);    
    // fread(inbuf, sizeof(char), sizeof(char) * SIZE, stdin);
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d", s + i);
    scanf("%d", &m);
    for (int i = 1, pos = 0; i <= m; ++i) {
        scanf("%d", &len[i]);
        st[i] = pos;
        for (int j = 0, cur; j < len[i]; ++j)
            scanf("%d", &p[pos++]);
        addnode(p[st[i]], i, st[i]);
    }    
    for (int i = 1; i <= n; ++i) {
        if (!h[s[i]]) continue;
        int t = h[s[i]];
        for (h[s[i]] = 0; t; t = q[t].next) {
            node c = q[t];
            if (c.p == st[c.s] + len[c.s] - 1) v[c.s] = true;
            else addnode(p[c.p + 1], c.s, c.p + 1);
        }
    }    
    for (int i = 1; i <= m; ++i) {
        if (v[i]) printf("Yes
");
        else printf("No
");
    }
    fclose(stdin);
    fclose(stdout);
    return 0;
}

谢谢收看， 祝身体健康！