二叉树基础框架
void traverse(TreeNode root){
traverse(root.left);//遍历左子树
traverse(root.right);//遍历右子树
}
//这个框架可以访问到树的每个节点
//相当一部分问题有对节点的操作,所以我们加入对节点操作的部分
void plusone(TreeNode root){
if(root==null)return;//这个是刹车
root.val=1;//这是对节点的操作
plusOne(root.right);//驱动区域
plusOne(root.left);//驱动区域
}
用到的题目
404.左叶子之和
54
108
Base模板升级
面试题68-II 二叉树的最近公共祖先
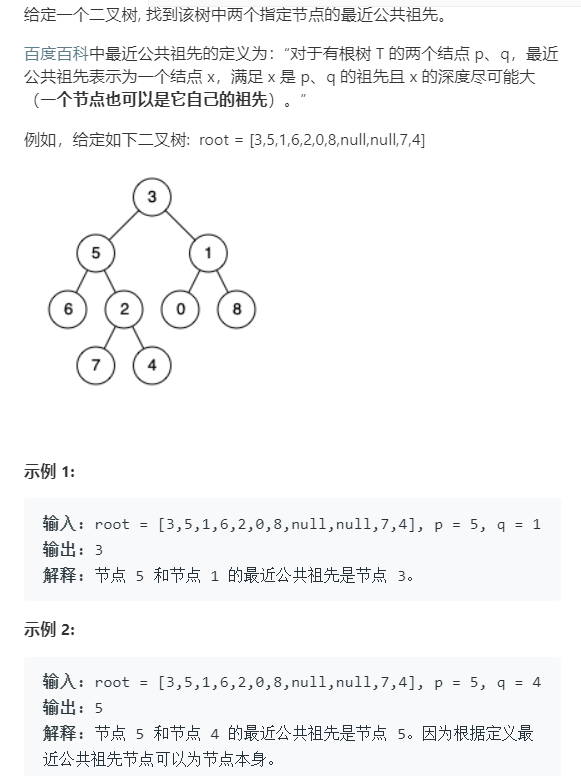
遇见这个题其实只要稍作分析就知道.
总共有三种情况.
左右子树各有一个节点
都在一个子树中 -> 都在左子树
-> 都在右子树
但是我们发现,要想实现这些内容似乎不能在节点操作区实现,因为一个节点根本无法判断这些内容.这个跟之后的操作有很多的关系.那怎么办呢?
答案如下:
class Solution {
TreeNode node;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//递归内部操作区(指定刹车等等)
if (root==null||root.val==p.val||root.val==q.val)return root;//找到就返回
//递归驱动器
TreeNode nodel= lowestCommonAncestor(root.left,p,q);
TreeNode noder=lowestCommonAncestor(root.right,p,q);
//递归结束操作区,对递归的值进行处理
if (nodel==null){
return noder;
}//左边不是返回右边
if (noder==null){
return nodel;
}//右边也不是返回左边
return root;//左右都是返回根节点
}
}
我们发现了我们将处理的方法放在了迭代去的下面
现在我们的模板又更新了
暂时为止的模板
class Solution {
TreeNode node;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
{刹车区:判定如何停止递归}
ex:
if (root == null) return 0;
{节点操作区:对节点进行操作(可选)}
{递归驱动区:用合理的操作让递归进行||根据函数的返回值将两个子树返回值保存下来,让他们们作为本函数的返回值}
ex:
int left_height = maxDepth(root.left);
int right_height = maxDepth(root.right);
//递归驱动区:一般来讲遇见返回值为Boolean的问题,我们都要将递归驱动使用&&或||连接符连在一起,例子如下:
iscure(left.left,right.right)&&iscure(left.right,right.left)
//这个值将作为返回值.(平时会写在递归返回区)
//这是因为这样可以将左右两个子树返回的值联系在一起,作为root的最终值.
//例子:965,112,671
//递归驱动区:遇见返回值为int的时候,你所应该考虑的是如何将每次递归产生的值传递到下一次递归中.其实和Boolean一样,我们也需要一些手段将左子树产生的值和右子树联系起来,最终形成对于root的操作.例子如下:
Math.max(depth(root.left), depth(root.right)) + 1;
//更多内容移步递归区代码扩充--返回int
//例题55-II
{递归后操作区:对于递归驱动区产生的值进行处理}
//列题:111,68-I,68-II
{递归返回区:确定返回的内容,如果想返回的值和题目要求返回的值不一样.就采用下面得战术.}
ex:
return Math.min(a,b);
}
}
//重写一个函数让题目给的函数调用他.
public boolean isSymmetric(TreeNode root) {
return iscure(root.left,root.right);
}
private int iscure(TreeNode left,TreeNode right){
return iscure(left.left,right.right)&&iscure(left.right,right.left);
}
递归驱动区代码扩充--返回int
遇见这种题一般有很多种可能,比较基础的就是跟树的深度有关.
对于这种问题其实很简单,就是运用刹车和递归驱动区让每次递归产生的值可以传递到下一次递归中.
if (root==null) return 0;//刹车区域
//递归驱动区域
a=isBalanced1(root.left);
b=isBalanced1(root.right);
//递归返回区域
return Math.max(a,b)+1;
我们发现,我们用在返回值上+1以及空节点返回值为0的手段,形成一个对于整个树深度的遍历.
然后用max函数将深度进行比较.也是将左右子树联系在一起.
当然,我么也可以在a和b上进行加减,然后返回.对于某些题是一种很好的解决方式.
(实际上,无论是Boolean还是int或者其他的,左右节点最终都要用一些办法将她们连接在一起.)
相关的题目:
55-I,55-II,111,104,110
递归驱动区---扩展变种
这种题最核心的感觉就是两棵树的比较
面试28:

因为实际上最终解决问题的时候要对两个树进行操作,所以本质来讲树的参数需要的遍历值时指数级上升的。如第一个二叉树,一开始只要输入root.left和root.right两个参数,到下一层就要输入root.left.left,root.left.right,root.right.left,root.right.right以此类推,下面的数量会越来越多.
所以当你意识到,这种比较方式不可能通过手动实现的时候.那就要开始自己行动了.那就是扩展参数.
你会发现实际上,从第一层到第二层是从1个参数,变成2个参数.第二层到第三层将会是4个参数.
所以不断地扩大参数是不现实的.
但是我们发现了一个规律,就是每层都比上次翻一番.这就是很好的解决办法.
class Solution {
public boolean isSymmetric(TreeNode root) {
//一层变成二层
return root==null?true:iscure(root.left,root.right);
}
public boolean iscure(TreeNode left,TreeNode right){
//处理部分已经删除
return iscure(left.left,right.right)&&iscure(left.right,right.left);
}
}
如上方法实际上就是依靠递归部分连接在一起,形成对于参数的扩充.
如下是原版的模板,比较一下区别.
iscure(left.left);
iscure(left.right);
相关题目:
101:对称二叉树
572:另一颗子树的子树
中间的节点操作部分也有一个值得记住的地方
这个判断方式可以轻松的发现左节点和右节点值不一样的问题.
if (left==null&&right==null)return true;
if(left == null || right == null) return false;
这个判断方式将是在之后经常出现的一种方式,先过滤掉左右都为空的情况.
剩下的情况就只剩下三种:
左空右有
左有右空
左有右有
所以完全可以用
if(left == null || right == null) return false;
来处理问题.
相关题目:
101:对称二叉树
572:另一颗子树的子树
以下是完整代码
class Solution {
public boolean isSymmetric(TreeNode root) {
return root==null?true:iscure(root.left,root.right);
}
public boolean iscure(TreeNode left,TreeNode right){
if (left==null&&right==null)return true;
if(left == null || right == null || left.val != right.val) return false;
return iscure(left.left,right.right)&&iscure(left.right,right.left);
}
}
运用到集合的题目
这些题目难度相对来说要大上一些,一般来讲运用到集合就是为了回溯.我们知道在递归的函数中是无法访问自己的根节点的,那么最好访问的办法就是将根节点的内容记录下来(放入容器中),让它传到参数中,或让其作为类的共有节点,将各个节点的值递归的加入集合之中.
例如:653
class Solution {
public boolean findTarget(TreeNode root, int k) {
List<Integer>list=new ArrayList<>();
return find(root, k, list);
}
private static boolean find(TreeNode root,int k,List<Integer> list){
if (root==null)return false;
if (list.contains(k-root.val)){//因为要求两数之和,所以直接用总数减去这个节点,剩下的值如果存在之前的值中,那就是可以的.
return true;
}
list.add(root.val);//将每个遍历过的节点放进list中.
return find(root.right,k,list)||find(root.left,k,list);
}
}
如上是比较简单的记录路径--被我称作单层集合,就是只用一个集合记录即可
公式为如下
List<Integer>list=new ArrayList<>();//声明一个集合
//传入之后的递归函数中
private static boolean find(TreeNode root,int k,List<Integer> list)
还有复杂的,就是用到两个集合,被我曾作双层集合.
这种集合也往往和迭代方式混用.
如:32-II
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();//一个集合传入要处理的节点
List<List<Integer>> res = new ArrayList<>();//一个集合传入处理后的数据
if(root != null) queue.add(root);//将根节点加入
while(!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();//退出一个处理集合中的节点
//对其进行处理
tmp.add(node.val);//将处理后的内容放入另一个集合中
if(node.left != null) queue.add(node.left);//驱动
if(node.right != null) queue.add(node.right);//驱动
}
res.add(tmp);
}
return res;
}
}//相关题目107,589,590
相关题目
653,32-II,
1022<-本题有些特殊,真正作为容器的是一个字符串,将字符串放进容器中.
107
700,938<-这个使用的是迭代
437
589
590
缩减代码量
{
if(s.val!=t.val)return false;//不涉及到刹车的部分可以直接写道return中
return
isSubtree1(s.left,t.left)
&&
isSubtree1(s.right,t.right);
}
{
return
t1.val == t2.val
&&
equals(t1.left, t2.left)
&&
equals(t1.right, t2.right);
}
这个内容是对上文的一个解释,关于如何将左右子树得出的结论联系在一起的
{
int left_height = maxDepth(root.left);
int right_height = maxDepth(root.right);
return java.lang.Math.max(left_height, right_height) + 1;
}
{
return max=1+Math.max(maxDepth(root.left),maxDepth(root.right));
}
//递归驱动区:一般来讲遇见返回值为Boolean的问题,我们都要将递归驱动使用&&或||连接符连在一起,例子如下:
iscure(left.left,right.right)&&iscure(left.right,right.left)
//这个值将作为返回值.(平时会写在递归返回区)
//这是因为这样可以将左右两个子树返回的值联系在一起,作为root的最终值.
//例子:965,112
//递归驱动区:遇见返回值为int的时候,你所应该考虑的是如何将每次递归产生的值传递到下一次递归中.其实和Boolean一样,我们也需要一些手段将左子树产生的值和右子树联系起来,最终形成对于root的操作.例子如下:
Math.max(depth(root.left), depth(root.right)) + 1;
//更多内容移步递归区代码扩充--返回int