Python 二分查找算法:
什么是二分查找,二分查找的解释:
二分查找又叫折半查找,二分查找应该属于减值技术的应用,所谓减值法,就是将原问题分成若干个子问题后,利用了规模为n的原问题的解与较小规模(通常是n/2)的子问题的解
之间的关系
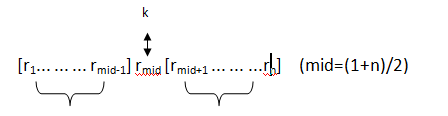
二分查找利用了记录关键码有序的特点,其基本思想为:在有序表中,取中间记录作为比较对象,若给定值与中间记录的关键码相等则查找成功:若给定值小与中间记录的关键码
则在中间记录的左半边继续查找;若给定值大于中间记录的关键码,则在中间记录右半边区继续查找。不断重复上述过程,直到查找成功,或所查找的区域无记录,查找失败。
二分查找的时间复杂度是O(log(n)),最坏情况下的时间复杂度是O(n)。
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
查找这个列表的66的索引位置,在不使用index情况下
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88] i = 0 for num in l: if num == 66: print(i) i+=1
如果列表有几十万或者几百万 这样查找的效率太低了
二分查找:
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
你观察这个列表,这是不是一个从小到大排序的有序列表呀?
如果这样,假如我要找的数比列表中间的数还大,是不是我直接在列表的后半边找就行了?

这就算是二分查找算法
那么落实的代码上我们怎么算呢
简单版:
l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88] def func(l,aim): mid = (len(l)-1)//2 if l: if aim > l[mid]: func(l[mid+1:],aim) elif aim < l[mid]: func(l[:mid],aim) elif aim == l[mid]: print("bingo",mid) else: print('找不到') func(l,66) func(l,6)
升级版:
l1 = [1, 2, 4, 5, 7, 9] def two_search(l,aim,start=0,end=None): end = len(l)-1 if end is None else end mid_index = (end - start) // 2 + start if end >= start: if aim > l[mid_index]: return two_search(l,aim,start=mid_index+1,end=end) elif aim < l[mid_index]: return two_search(l,aim,start=start,end=mid_index-1) elif aim == l[mid_index]: return mid_index else: return '没有此值' else: return '没有此值' print(two_search(l1,9))