省选前的动态规划大杂烩

这是一个不知道为什么反正就是想写成汇总的东西，整合一些DP题(其实是懒得一个个写题解)

因为沙茶博主DP很菜(什么都很菜，只是DP尤其菜)又做题少，所以写了这样一个记录沙茶博主在省选退役前刷的DP题的东西

一些零碎的知识点在知识总结里

好像上一行两句没有什么因果关系

好了沙茶博主把DP知识点也丢进这个东西里了，感觉这个可以拿来学(虽然除了沙茶自己没人看这玩意)，因为沙茶博主写的时候基本那些东西都不扎实，跟重新学了一遍差不多

---

前一阵的链接们：

虚树DP：SDOI 2011 消耗战 HNOI 2014 世界树

凸优化：八省联考2018 林克卡特树

决策单调性：NOI 2009 诗人小G

树形DP：CF1118F2 Tree Cutting 国家集训队 Crash的文明世界

乱七八糟的东西们：九省联考2018 CoaT(写的暴力) WC 2018 州区划分(并没搞太懂)  

----------------------------------------------------------

HAOI 2011 problem a

转化

注意每个人的分数区间不可相交，然后莫得了

#include<map>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100005,inf=1e9; 
struct a
{
    int ll,rr,val;
}mem[N];
int n,t1,t2,cnt,ans,va[N],maxi[4*N];
map<pair<int,int>,int> mp;
void Mini(int &x,int y)
{
    if(x>y) x=y;
}
bool cmp(a x,a y)
{
    return x.ll==y.ll?x.rr<y.rr:x.ll<y.ll;
}
void Count(int l,int r)
{
    pair<int,int> pr=make_pair(l,r);
    if(!mp.count(pr)) mp[pr]=++cnt;
    int id=mp[pr]; va[id]++;
    mem[id]=(a){l,r,va[id]};
}
void Change(int nde,int l,int r,int pos,int tsk)
{
    if(l==r)
        maxi[nde]=tsk; 
    else
    {
        int mid=(l+r)>>1,ls=2*nde,rs=2*nde+1;
        if(pos<=mid) Change(ls,l,mid,pos,tsk);
        else Change(rs,mid+1,r,pos,tsk);
        maxi[nde]=max(maxi[ls],maxi[rs]);
    }
}
int Query(int nde,int l,int r,int ll,int rr)
{
    if(l>rr||r<ll)
        return -inf;
    else if(l>=ll&&r<=rr)
        return maxi[nde];
    else
    {
        int mid=(l+r)>>1,ls=2*nde,rs=2*nde+1;
        return max(Query(ls,l,mid,ll,rr),Query(rs,mid+1,r,ll,rr));
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&t1,&t2);
        if(t2+1>n-t1) continue;
        Count(t2+1,n-t1);
    }
    for(int i=1;i<=cnt;i++)
        Mini(mem[i].val,mem[i].rr-mem[i].ll+1);
    sort(mem+1,mem+1+cnt,cmp);
//    for(int i=1;i<=cnt;i++) printf("%d %d %d
",mem[i].ll,mem[i].rr,mem[i].val);
    for(int i=1;i<=cnt;i++)
    {
        int qry=Query(1,0,n,0,mem[i].ll-1);
        int newa=qry+mem[i].val;
        Change(1,0,n,mem[i].rr,newa),ans=max(ans,newa);
    }
    printf("%d ",n-ans);
    return 0;
}

NOI 2015 寿司晚宴

转化

互质归根结底是没有相同质因数，而每个数只可能有一个大于$sqrt n$的质因数。搞出来每个数小于$sqrt n$的质因数的状态和(是否有)大于$sqrt n$的质因数，按后者从小到大排序，大于$sqrt n$的质因数相同的一块DP(没有的每个单独DP)。然后基本莫得了，注意容斥掉两个人都没选的情况

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=510,M=260,all=255;
const int pri[8]={2,3,5,7,11,13,17,19};
long long n,mod,cnt,ans,dp[M][M],fir[M][M],sec[M][M];
struct a
{
    int sta,hug;
}num[N];
bool cmp(a x,a y)
{
    return x.hug==y.hug?x.sta<y.sta:x.hug<y.hug;
}
void Add(long long &x,long long y)
{
    x+=y;
    if(x>=mod) x-=mod;
}
void Pre()
{
    for(int i=2;i<=n;i++)
    {
        int tmp=i;
        for(int j=0;j<=7;j++)
            if(tmp%pri[j]==0)
            {
                num[i].sta|=1<<j;
                while(tmp%pri[j]==0) tmp/=pri[j];
            }
        num[i].hug=tmp;
    }
    sort(num+2,num+1+n,cmp),dp[0][0]=1;
}
int main()
{
    scanf("%lld%lld",&n,&mod),Pre();
    for(int i=2;i<=n;i++)
    {
        if(i==2||num[i].hug==1||num[i].hug!=num[i-1].hug)
        {
            for(int j=0;j<=all;j++)
                for(int k=0;k<=all;k++)
                    fir[j][k]=sec[j][k]=dp[j][k];
        }
        for(int j=all;~j;j--)
            for(int k=all;~k;k--)
                if(!(j&k))
                {
                    if(!(k&num[i].sta)) Add(fir[j|num[i].sta][k],fir[j][k]);
                    if(!(j&num[i].sta)) Add(sec[j][k|num[i].sta],sec[j][k]);
                }
        if(i==n||num[i].hug==1||num[i].hug!=num[i+1].hug)
        {
            for(int j=all;~j;j--)
                for(int k=all;~k;k--)
                    if(!(j&k)) dp[j][k]=(fir[j][k]+sec[j][k]-dp[j][k]+mod)%mod;
        }
    }
    for(int i=0;i<=all;i++)
        for(int j=0;j<=all;j++)
            if(!(i&j)) Add(ans,dp[i][j]);
    printf("%lld",ans);
    return 0;
}

SCOI 2014 方伯伯的玉米田

分析

直接做不可做，分析性质，发现每次一定是拔一个后缀。因为后面不比它矮的拔了不会使答案变劣，后面比它矮的拔了还是没贡献，最后还拔走就行。

于是可以设计一个DP：$dp[i][j]$表示到$i$为止(i被)拔了$j$次的最长不下降子序列，转移为：

$dp[i][j]=max(dp[i][j],dp[k][h]+1)(a[i]+j>a[k]+h&&j>h)$

树状数组维护二维(前缀)最大值

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=10005,M=505;
int n,k,mx,ans,a[N],bit[N][M];
int Query(int x,int y)
{
    int ret=0;
    for(int i=x;i;i-=i&-i)
        for(int j=y;j;j-=j&-j)
            ret=max(ret,bit[i][j]);
    return ret;
}
void Change(int x,int y,int v)
{
    for(int i=x;i<=mx+k;i+=i&-i)
        for(int j=y;j<=k;j+=j&-j)
            bit[i][j]=max(bit[i][j],v);
}
int main()
{
    scanf("%d%d",&n,&k),k++;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),mx=max(mx,a[i]);
    for(int i=1;i<=n;i++)
        for(int j=k;j;j--)
        {
            int len=Query(a[i]+j,j)+1;
            ans=max(ans,len),Change(a[i]+j,j,len);
        }
    printf("%d ",ans);
    return 0;
}

IOI 2005 河流

对未来的承诺

因为当前节点的决策影响了之后父亲的决策，一般设状态转移不了。所以在dp状态里先对未来承诺：设$dp[i][j][k]$表示以$i$为根的子树里放了$k$个伐木场，承诺$i$上面的第一个伐木场是$j$的最小代价，然后每次在当前节点到根的链上DP。

不知为何转移时加上子树size的限制就错了

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=110,M=55;
int n,m,t1,t2,cnt,top;
int p[N],noww[N],goal[N],val[N];
int wood[N],dep[N],stk[N],dp[N][N][M];
void Mini(int &x,int y)
{
    if(x>y) x=y;
}
void Link(int f,int t,int v)
{
    noww[++cnt]=p[f],p[f]=cnt;
    goal[cnt]=t,val[cnt]=v;
}
void DFS(int nde)
{
    stk[++top]=nde;
    for(int i=p[nde];i;i=noww[i])
    {
        int g=goal[i];
        dep[g]=dep[nde]+val[i],DFS(g);
        for(int j=1;j<=top;j++)
            for(int k=m;~k;k--)
            {
                int anc=stk[j];
                dp[nde][anc][k]+=dp[g][anc][0];
                for(int h=1;h<=k;h++)
                    Mini(dp[nde][anc][k],dp[nde][anc][k-h]+dp[g][anc][h]);
            }    
    }
    top--;
    for(int i=1;i<=top;i++)
    {
        int anc=stk[i],cst=wood[nde]*(dep[nde]-dep[anc]);
        dp[nde][anc][0]+=cst;
        for(int j=1;j<=m;j++)
            dp[nde][anc][j]=min(dp[nde][anc][j]+cst,dp[nde][nde][j-1]);
    }
}
int main()
{
    scanf("%d%d",&n,&m),n++;
    for(int i=2;i<=n;i++)
        scanf("%d%d%d",&wood[i],&t1,&t2),Link(t1+1,i,t2);
    DFS(1),printf("%d",dp[1][1][m]);
    return 0;
}

HNOI 2007 梦幻岛宝珠

明示你按$b$分组，每组内先做背包再合并起来。合并就是从低位向高位合并，同时注意m的这一位是否有值

// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,t1,t2,len;
long long dp[35][1100];
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        if(n==-1) break;
        memset(dp,len=0,sizeof dp);
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d",&t1,&t2); int pw=0;
            while(t1%2==0) t1/=2,pw++; 
            for(int j=1000;j>=t1;j--)    
                dp[pw][j]=max(dp[pw][j],dp[pw][j-t1]+t2);
        }
        int tmp=m;
        while(tmp) tmp>>=1,len++; len--;
        for(int i=1;i<=len;i++)
            for(int j=1000;~j;j--)
                for(int k=0;k<=j;k++)
                {
                    int lst=min(1000,(k<<1)+((m>>(i-1))&1));
                    dp[i][j]=max(dp[i][j],dp[i][j-k]+dp[i-1][lst]);
                }
        printf("%lld
",dp[len][1]);
    }
    return 0;
}

洛谷 P5241 序列

这题好的

我直接转洛谷题解了

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=410,mod=1e9+7;
int n,m,nm,lim[N];
int f1[2][N][N],s1[N][N];
int f2[2][N],s2[N],ans[N*N];
int Add(int x,int y)
{
    x+=y;
    if(x>=mod) x-=mod;
    return x;
}
void Write(int x)
{
    if(x>9) Write(x/10);
    putchar(x%10|48);
}
int main()
{
    register int i,j,k;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        lim[i]=(n-i+1)*(n-1)+(i-1)*(i-2)/2;
    auto p1=f1[0],p2=f1[1]; 
    m=n*min(2,n-1),nm=n*(n-1),ans[1]=p2[n][1]=1;
    for(i=1;i<=n;i++) s1[n][1]=1;
    for(i=2;i<=m;i++)
    {
        for(j=1;j<=n;j++)
            if(i<=lim[j])
                for(k=1;k<=n;k++)
                    if(i-k+1>=n-j)
                        p1[j][k]=Add(p2[j][k],s1[j+1][k-1]);
        for(j=n;j;j--)
            for(k=1;k<=n;k++)
            {
                s1[j][k]=Add(s1[j+1][k],p1[j][k]);
                ans[i]=Add(ans[i],p1[j][k]),p2[j][k]=0;
            }
        swap(p1,p2);
    }
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            f2[1][i]=Add(f2[1][i],p2[i][j]),s2[i]=Add(s2[i],s1[i][j]);
    auto q1=f2[0],q2=f2[1];
    for(i=m+1;i<=nm;i++)
    {
        for(j=1;j<=n;j++)
            if(i<=lim[j])
                q1[j]=Add(q2[j],s2[j+1]);
        for(j=n;j;j--)
        {
            s2[j]=Add(s2[j+1],q1[j]);
            ans[i]=Add(ans[i],q1[j]),q2[j]=0;
        }
        swap(q1,q2);
    }
    for(i=1;i<=nm;i++) Write(ans[i]),putchar(' ');
    return 0;
}

洛谷 P4890 Never·island

学了一个处理这种序列上线段乱搞问题的套路

把每个线段抽象成一个点，线段本身分成左右端点讨论建图，最后把问题转成一个图上问题

这里把线段的左右端点从大到小排序后讨论每个点$x$和它的下一个点$y$：

如果$x$是左端点，$y$是右端点：如果$x,y$就是一条线段直接把点权加上长度；否则用权值为长度的边连接$x->y$所代表的线段，表示他们中间这段如果给$y$队钥匙是可以省掉的

如果两个都是左/右端点就把左/右边那个的点权加上长度

如果$x$是右端点，$y$是左端点，那么说明这中间是断开的，直接贡献进去

最后我们得到了一坨链，就可以依次DP这些链了。设$dp[i][j][2]$表示决策到第$i$个队伍给出去$j$把钥匙，当前队伍给没给钥匙，$O(n^2)$DP即可

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=4005;
struct a
{
    int typ,pos,idx;
}pts[N];
bool cmp(a x,a y)
{
    return x.pos<y.pos;
}
int n,m,t1,t2,cnt,tot,mem;
int per[N],vis[N],dp[2][N][N];
int pre[N],nxt[N],val[N],len[N],deg[N];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&t1,&t2);
        pts[++cnt]=(a){0,t1,i};
        pts[++cnt]=(a){1,t2,i};
    }
    sort(pts+1,pts+1+cnt,cmp);
    for(int i=1;i<cnt;i++)
    {
        a a1=pts[i],a2=pts[i+1];
        int lth=a2.pos-a1.pos,x=a1.idx,y=a2.idx;
        int xx=a1.typ,yy=a2.typ;
        if(!xx&&yy) 
        {
            if(x==y) mem+=lth;
            else pre[y]=x,nxt[x]=y,len[x]=lth,deg[y]++;
        }
        else if(!xx&&!yy) val[x]+=lth;
        else if(xx&&yy) val[y]+=lth;
        else mem+=lth;
    }
    for(int i=1;i<=cnt;i++)
        if(!vis[pts[i].idx]&&!deg[pts[i].idx])
        {
            int nde=pts[i].idx;
            per[++tot]=nde,vis[nde]=true;
            while(nxt[nde]) nde=nxt[nde],per[++tot]=nde,vis[nde]=true;
        }
    auto p1=dp[0],p2=dp[1];
    for(int i=1;i<=n;i++)
    {
        int nde=per[i];
        for(int j=1;j<=m;j++)
        {
            p1[i][j]=max(p1[i-1][j],p2[i-1][j]);
            if(!pre[nde]) p2[i][j]=max(p1[i-1][j-1],p2[i-1][j-1])+val[nde];
            else p2[i][j]=max(p1[i-1][j-1],p2[i-1][j-1]+len[pre[nde]])+val[nde];
        }
    }
    printf("%d",pts[cnt].pos-pts[1].pos-max(p1[n][m],p2[n][m])-mem);
    return 0;
}

洛谷 P2300 合并神犇

我太菜了，被高一学长吊打了

(按着一个错误的沙雕思路WA了一大串

设$dp[i]$表示合并到i为止的最少合并次数，转移是$dp[i]=dp[j]+i-j-1$，其中$j$是最靠后的满足$sum[i]-sum[j]>=lst[j]$的位置，$lst[j]$表示到$j$为止的最后一个数

显然移项之后就要找满足$sum[i]>=sum[j]+lst[j]$的最大的j，然后我不知道怎么想的认为这个东西可以set搞(显然tm是假的，就开始摁着改。

都省选了怎么还有这么制杖的人？

事实上权值线段树即可，注意开long long

#include<set>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define lli long long
using namespace std;
const int N=200005;
int n,tot,root;
lli sum[N],dp[N],lst[N];
int val[48*N],son[48*N][2]; 
int Query(int &nde,lli l,lli r,lli ll,lli rr)
{
    if(l>=ll&&r<=rr)
        return val[nde];
    else 
    {
        lli mid=(l+r)>>1;int ret=0;
        if(mid>=ll) ret=max(ret,Query(son[nde][0],l,mid,ll,rr));
        if(mid<rr) ret=max(ret,Query(son[nde][1],mid+1,r,ll,rr)); 
        val[nde]=max(val[son[nde][0]],val[son[nde][1]]); return ret;
    }
}
void Insert(int &nde,lli l,lli r,lli pos,int tsk)
{
    if(!nde) nde=++tot;
    if(l==r) 
        val[nde]=max(val[nde],tsk);
    else
    {
        lli mid=(l+r)>>1;
        if(pos<=mid) Insert(son[nde][0],l,mid,pos,tsk);
        else Insert(son[nde][1],mid+1,r,pos,tsk); 
        val[nde]=max(val[son[nde][0]],val[son[nde][1]]);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%lld",&sum[i]),sum[i]+=sum[i-1];
    Insert(root,0,sum[n],0,0);
    for(int i=1;i<=n;i++)
    {
        int pos=Query(root,0,sum[n],0,sum[i]);
        dp[i]=dp[pos]+i-pos-1,lst[i]=sum[i]-sum[pos];
        if(lst[i]+sum[i]<=sum[n]) Insert(root,0,sum[n],lst[i]+sum[i],i);
    }
//    for(int i=1;i<=n;i++) printf("%d ",dp[i]);puts("");
//    for(int i=1;i<=n;i++) printf("%d ",lst[i]);puts("");
    printf("%lld",dp[n]);
    return 0;
}

---

各种DP及他们的优化

DP优化的本质要么是删状态要么是改转移(废话

感觉DP这个东西更重理解

1.线性DP(基本看的Flashhu的博客)

就是当前的DP值由前面一个DP值加上个代价转移过来，这种DP我统称为线性DP

优化们

①做前缀和

这好像是通用的......例题的话 逆序对数列

②单调队列

1.转移是一块区间，而且区间单调地移动

2.当前不优的转移点将来一定不会更优

所以维护一个合法转移点的区间，每次从队头踢掉不合法的点，用队头更新，然后从队尾加入当前点，顺便把所有不优的都踢掉

例题有什么 瑰丽华尔兹 和 股票交易 之类的

这东西可以用来优化多重背包，对每个物品维护同余的单调队列，比二进制压缩还快那么一个log，然并卵

③数据结构优化

有个经典的东西叫做线段树优化DP

这种有时候会和单调线性结构结合

比如说 USACO12OPEN Bookshelf

现在感觉当时写麻烦了，可以看这个

线段树不仅是可以优化复杂度，还有整合信息的作用

比如说 CF833B The Bakery

④决策单调性优化

顾名思义，DP的决策点单调移动

有两种优化方法：单调线性结构(栈或队列)或者分治

(其实本质上没有区别，看你写哪个)

分治就记录当前求解区间和当前决策区间，每次暴力扫出来当前的最优决策点，往下递归就完了

好像是雅礼集训的题 珠宝(体积很小的01背包)

#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int N=1000005,M=305;
ll tr1[N],tr2[N],tmp[N],tep[N],sum[N];
int n,m,t1,t2,sz,mx; vector<int> ve[M];
bool cmp(ll a,ll b)
{
    return a>b;
}
void Solve(ll *lst,ll *cur,int l,int r,int nl,int nr)
{
    if(l>r) return;
    if(nl==nr)
        for(int i=l;i<=r;i++)    
            cur[i]=lst[nl]+sum[i-nl];
    else 
    {
        if(l==r)
        {
            cur[l]=0; int lp=max(nl,l-sz),rp=min(nr,l);
            for(int i=lp;i<=rp;i++)
                cur[l]=max(cur[l],lst[i]+sum[l-i]);
        }
        else
        {
            int mid=(l+r)/2; cur[mid]=0;
            int pt=-1,lp=max(nl,mid-sz),rp=min(nr,mid);
            for(int i=lp;i<=rp;i++)
            {
                ll val=lst[i]+sum[mid-i];
                if(val>=cur[mid])
                    cur[mid]=val,pt=i;
            }
            Solve(lst,cur,l,mid-1,nl,pt);
            Solve(lst,cur,mid+1,r,pt,nr);
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&t1,&t2);
        ve[t1].push_back(t2),mx=max(mx,t1);
    }
    mx=min(mx,m); ll *dp=tr1,*pd=tr2;
    for(int i=1;i<=mx;i++)
        if(!ve[i].empty())
        {
            sz=ve[i].size();
            sort(ve[i].begin(),ve[i].end(),cmp);
            for(int j=1;j<=sz;j++)
                sum[j]=sum[j-1]+ve[i][j-1];
            for(int j=0,p;j<i;j++)
            {
                p=0; for(int k=j;k<=m;k+=i) tmp[++p]=dp[k];
                Solve(tmp,tep,1,p,1,p);
                p=0; for(int k=j;k<=m;k+=i) pd[k]=tep[++p];
            }
            for(int j=0;j<i;j++) pd[j]=dp[j]; swap(dp,pd);
        }
    for(int i=1;i<=m;i++)
        dp[i]=max(dp[i-1],dp[i]),printf("%lld ",dp[i]);
    return 0;
}

线性结构的话如果之前的决策区间不会过期可以决策栈，否则决策队列

类似单调队列的操作，就是注意弹队尾的时候可能最后一个决策区间是弹了一部分，要二分一下

NOI 2009 诗人小G

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define lli long long
#define double long double
using namespace std;
const int N=100005;
const lli inf=1e18;
struct a
{
    int l,r,p;
}que[N];
int T,n,m,k,f,b,top,pre[N],stk[N]; 
lli len[N]; double dp[N]; char str[N][32];
double Qpow(double x,int k)
{
    if(k==1) return x;
    double tmp=Qpow(x,k/2);
    return k%2?tmp*tmp*x:tmp*tmp;
}
double Calc(int a,int b)
{
    return dp[b]+Qpow(fabs(len[a]-len[b]-m-1),k);
}
int main()
{ 
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&k);
        for(int i=1;i<=n;i++)
        {
            scanf("%s",str[i]+1);
            len[i]=len[i-1]+strlen(str[i]+1)+1;
        }
        que[f=b=0]=(a){1,n,0};
        for(int i=1;i<=n;i++)
        {
            while(f<b&&que[f].r<i) f++;
            int pt=que[f].p; que[f].l++;
            dp[i]=Calc(i,pt),pre[i]=pt;
            while(f<b&&Calc(que[b].l,que[b].p)>=Calc(que[b].l,i)) b--;
            int lp=que[b].l,rp=que[b].r,ps=rp+1;
            while(lp<=rp)
            {
                int mid=(lp+rp)/2;
                if(Calc(mid,i)<=Calc(mid,que[b].p)) rp=mid-1,ps=mid;
                else lp=mid+1;
            }
            (ps==que[b].l)?b--:que[b].r=ps-1;
            if(ps<=n) que[++b]=(a){ps,n,i};
        }
        if(dp[n]>inf) puts("Too hard to arrange");
        else
        {
            printf("%lld
",(lli)dp[n]),top=0;
            for(int i=n;i;i=pre[i]) stk[++top]=i; stk[++top]=0; 
            for(int i=top;i;i--)
                for(int j=stk[i+1]+1;j<=stk[i];j++)
                {
                    printf("%s",str[j]+1);
                    j==stk[i]?puts(""):putchar(' ');
                }
        }
        puts("--------------------");
    }
    return 0;
}

其实四边形不等式也可以归进决策单调性来

这玩意用的时候可能打决策表瞪眼比较好

如果有个DP实在不知道怎么优化可以胡猜它满足四边形不等式，再把边界放宽一点，乱搞技巧.JPG

⑤斜率优化

从这里开始我们数形结合了

感觉这东西非常让人(wo)头大

首先，我觉得也是最让人头大的(可能我脑回路不太正常)，什么^他娘的叫斜率优化？

这种DP的转移一般形如$dp[i]=max{dp[j]+a[i]*b[j]+c[j]+d[i]}$，$a,b,c,d$都是和下标有关的变量(当然那个max可以是min)

显然和j无关的在这个转移里都不用管，我们把剩下的东西分类整合一下

$(a[i]*b[j])+(dp[j]+c[j])$

那我们先说为什么会扯到斜率

如果你高一没有一直停课，你应该听你的高中数学老师讲过一个叫做线性规划的东西

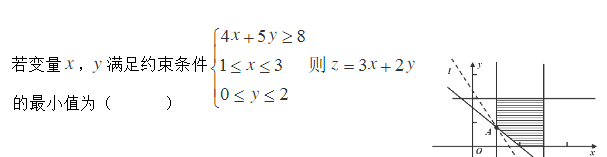
就像上面这种玩意，图是百度随便找的

你把可行区域画出来，拿那条直线去切它，找截距的最值

所以呢？这和斜率优化有什么关系？

我们把每个位置的dp值看做一个二维平面上的点......

怎么就看做点了呢？

个人觉得最好理解的方法是直接倒腾那个式子，因为dp[j]+c[j]都只和j有关，我们就把它们统称f[j]

我们假设从n转移比从m转移要优，那么就有

$a[i]*b[n]+f[n]>a[i]*b[m]+f[m]$

$f[n]-f[m]>a[i]*(b[m]-b[n])$

$frac{f[n]-f[m]}{b[n]-b[m]}<-a[i]$

所以上面那个式子成立的时候从n转移比从m转移优

现在如果我们把f(即只和转移点有关的项)看做x坐标，b(即一开始既和转移点有关又与当前位置有关的项)看做y坐标，左边的东西就是一个斜率

那对应的我们把右边的-a[i]也看做是斜率，所有转移就是一堆以-a[i]为斜率的直线，实际进行转移的是每条直线的截距

我们说完了什么是斜率，然后怎么优化呢？

暴力做转移就是拿那个斜率在每个点都试一试

优化？想想那道高考题

显然只要在边上的点试一试就好了，当然，我们都知道这些点组成的这个东西叫做— —

凸包

现在的问题就是— —

1.维护好凸包 2.在凸包上找答案

找答案是一个通用的过程，所以斜率优化优化来优化去就是在— —

维护凸包

(下面这段话假设了每次新来的横坐标和询问斜率都单调)

我们找一个单调线性结构(参考决策单调性优化DP)存储凸包上的点，以单调队列为例，对于每个点

1.按照推出来的那个式子更新队头

2.更新答案

3.把那些将来不可能成为凸包上的点的点从队尾踢掉

问题又来了

我刚才说“下面这段话假设了每次新来的横坐标和询问斜率都单调”

那如果询问斜率不单调怎么办？

也就是说队头不能pop，那我们总不能每次暴力扫凸包吧

当然不，斜率不单调也是有一个最优点的，可以二分这个最优点

那如果新来的横坐标不单调怎么办？

也就是说做着做着突然发现前面又出来一个点

按时间CDQ分治，每层里把左半边按横坐标排序建凸包，把右半边放上去跑，然后递归右半边

可以看CEOI2017 Building Bridges

#include<cstdio>
#include<cstring>
#include<algorithm>
#define lli long long
using namespace std;
const int N=100005;
int n,top,pos[N],stk[N];
lli h[N],s[N],x[N],y[N],dp[N];
void Maxi(lli &x,lli y){if(x<y) x=y;}
void Mini(lli &x,lli y){if(x>y) x=y;}
bool cmp(int a,int b)
{
    return x[a]==x[b]?y[a]<y[b]:x[a]<x[b];
}
bool Slope(int a,int b,int c)
{
    return (y[a]-y[c])*(x[b]-x[c])>=(y[b]-y[c])*(x[a]-x[c]);
}
lli Calc(int a,int b)
{
    return -2*h[b]*x[a]+y[a];
}
void CDQ(int l,int r)
{
    if(l==r)
        x[l]=h[l],y[l]=dp[l]-s[l]+h[l]*h[l]; 
    else
    {
        int mid=(l+r)>>1;
        CDQ(l,mid);
        sort(pos+l,pos+1+mid,cmp),top=0;
        for(int i=l;i<=mid;i++)
        {
            while(top>1&&Slope(pos[i],stk[top-1],stk[top])) top--;
            stk[++top]=pos[i];
        }
        for(int i=mid+1;i<=r;i++)
        {
            int ll=1,rr=top-1,re=top;
            while(ll<=rr)
            {
                int midd=(ll+rr)>>1;
                if(Calc(stk[midd],i)<Calc(stk[midd+1],i)) re=midd,rr=midd-1;
                else ll=midd+1;
            }
            Mini(dp[i],Calc(stk[re],i)+s[i-1]+h[i]*h[i]);
        }
        CDQ(mid+1,r);
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lld",&h[i]);
    for(int i=1;i<=n;i++) scanf("%lld",&s[i]);
    for(int i=1;i<=n;i++) pos[i]=i,s[i]+=s[i-1];
    memset(dp,0x3f,sizeof dp),dp[1]=0;
    CDQ(1,n),printf("%lld",dp[n]);
    return 0;
}

终于在省选前两周学完了斜率优化，wsl

2.选取物品型的DP

前面说的同余单调队列优化多重背包和决策单调性优化(特定的)01背包

二进制压缩多重背包

NOIP内容，不说了

凸优化

例题：八省联考2018 林克卡特树

以选取的个数为为x轴，最优解为y轴。如果这是个上凸函数，这种DP有个套路的优化方法叫做凸优化：二分斜率，然后我们强制选取物品时额外付出斜率的代价。把原来的DP当成一个输入斜率输出切点的黑箱，相当于不限制数目地选取。最后得到一个最优情况下选出来的数目，根据这个数目调整二分上下界即可。

树形背包

虽然这样不好，但我还是要借一个东西来说一个沙茶原来不会的技巧

— —九省联考2018 CoaT(指统计这种贡献的方法)

多项式卷积优化

经常与生成函数一起用

对未来的承诺

如果当前的选取决策影响将来的选取，可以在状态里对将来进行承诺

比如IOI2005河流

3.其他奇奇怪怪的DP 

状压DP

呃，没啥可说的？

看到范围很小记得想这个就行

数位DP

套路

看到了别忘了套路就行

(以上两种可以去洛谷博客找一找)

虚树DP

估计出了我又不会

至少记得怎么建虚树吧

(看博客去)

动态DP(DDP)

看NOIP2018保卫王国的题解

插头DP

状压走人，再问不会

斯坦纳树

看博客.jpg

所以最后这些就是让人去翻博客的=。=？？？