R语言-朴素贝叶斯

我们还是用相亲网站的数据来建立模型预测一个人是否约会成功：

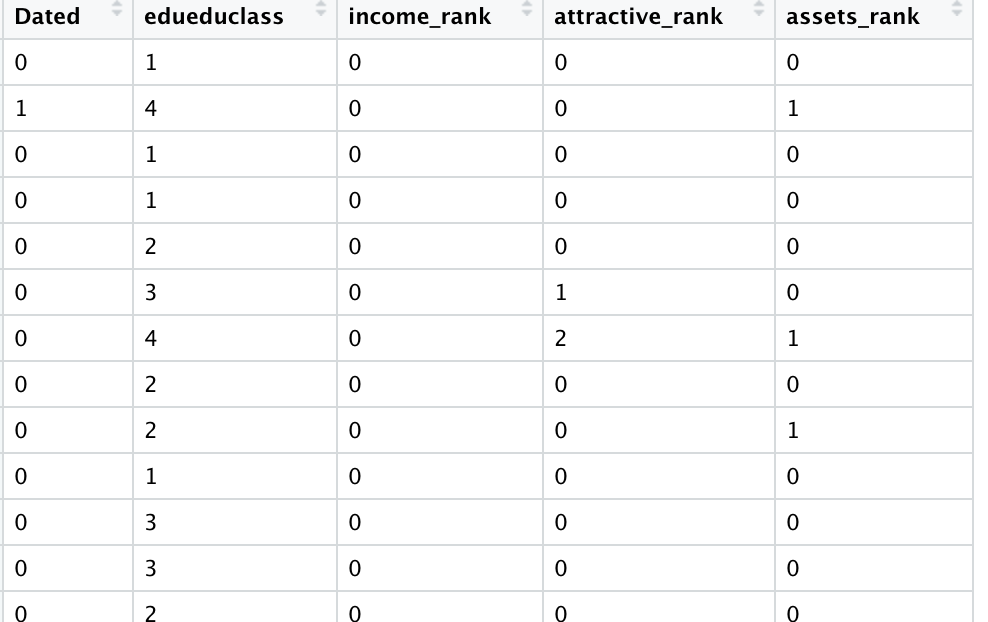
根据大数定律我们知道当数据足够多的时候频率等于概率，所以数据越大，我们用贝叶斯算法预测的越准确

> ##加载数据集:相亲网站约会数据
> setwd("/Users/yaozhilin/Downloads/R_edu/data")
> Data<-read.csv("date_data2.csv")
> data<-Data[,c(5,4,6,7,8)]
> #朴素贝叶斯需要数据都是等级变量
> data<-as.data.frame(lapply(data, as.factor))#需要lapply作用于数据的每个元素
> #选择训练集和测试集
> set.seed(123)
> sample<-sample(1:nrow(data),length(data$Dated)*0.6)
> train<-data[sample,]
> test<-data[-sample,]
> #加载调用bayes函数的包
> library(e1071)
> #用train训练得到模型
> bayesmodel<-naiveBayes(Dated~income_rank+attractive_rank+assets_rank,train)
> #用模型来预测test中Dated数据
> pre<-predict(bayesmodel,test)
> #查看预测结果的准确率
> table(pre,test$Dated)
   
pre  0  1
  0 15  5
  1  2 18
> accuracy<-sum(pre==test$Dated)/length(test$Dated)#准确率
> accuracy
[1] 0.825
> library(gmodels)
> table<-CrossTable(test$Dated,pre)

 
   Cell Contents
|-------------------------|
|                       N |
| Chi-square contribution |
|           N / Row Total |
|           N / Col Total |
|         N / Table Total |
|-------------------------|

 
Total Observations in Table:  40 

 
             | pre 
  test$Dated |         0 |         1 | Row Total | 
-------------|-----------|-----------|-----------|
           0 |        15 |         2 |        17 | 
             |     4.971 |     4.971 |           | 
             |     0.882 |     0.118 |     0.425 | 
             |     0.750 |     0.100 |           | 
             |     0.375 |     0.050 |           | 
-------------|-----------|-----------|-----------|
           1 |         5 |        18 |        23 | 
             |     3.674 |     3.674 |           | 
             |     0.217 |     0.783 |     0.575 | 
             |     0.250 |     0.900 |           | 
             |     0.125 |     0.450 |           | 
-------------|-----------|-----------|-----------|
Column Total |        20 |        20 |        40 | 
             |     0.500 |     0.500 |           | 
-------------|-----------|-----------|-----------|

 
> table$prop.row[2,2]#召回率
[1] 0.7826087
> table$prop.col[2,2]#命中率
[1] 0.9

总结:切记特征条件是独立的，数据要足够大才能使用朴素贝叶斯定理

> ##加载数据集:相亲网站约会数据> setwd("/Users/yaozhilin/Downloads/R_edu/data")> Data<-read.csv("date_data2.csv")> data<-Data[,c(5,4,6,7,8)]> #朴素贝叶斯需要数据都是等级变量> data<-as.data.frame(lapply(data, as.factor))#需要lapply作用于数据的每个元素> #选择训练集和测试集> set.seed(123)> sample<-sample(1:nrow(data),length(data$Dated)*0.6)> train<-data[sample,]> test<-data[-sample,]> #加载调用bayes函数的包> library(e1071)> #用train训练得到模型> bayesmodel<-naiveBayes(Dated~income_rank+attractive_rank+assets_rank,train)> #用模型来预测test中Dated数据> pre<-predict(bayesmodel,test)> #查看预测结果的准确率> table(pre,test$Dated)   pre  0  1  0 15  5  1  2 18> accuracy<-sum(pre==test$Dated)/length(test$Dated)#准确率> accuracy[1] 0.825> library(gmodels)> table<-CrossTable(test$Dated,pre)
    Cell Contents|-------------------------||                       N || Chi-square contribution ||           N / Row Total ||           N / Col Total ||         N / Table Total ||-------------------------|
 Total Observations in Table:  40 
              | pre   test$Dated |         0 |         1 | Row Total | -------------|-----------|-----------|-----------|           0 |        15 |         2 |        17 |              |     4.971 |     4.971 |           |              |     0.882 |     0.118 |     0.425 |              |     0.750 |     0.100 |           |              |     0.375 |     0.050 |           | -------------|-----------|-----------|-----------|           1 |         5 |        18 |        23 |              |     3.674 |     3.674 |           |              |     0.217 |     0.783 |     0.575 |              |     0.250 |     0.900 |           |              |     0.125 |     0.450 |           | -------------|-----------|-----------|-----------|Column Total |        20 |        20 |        40 |              |     0.500 |     0.500 |           | -------------|-----------|-----------|-----------|
 > table$prop.row[2,2]#召回率[1] 0.7826087> table$prop.col[2,2]#命中率[1] 0.9