大致可以总结如下:
- 前序排列(preorder):根左右
- 中序排列(inorder):左根右
- 后续排序(postorder):左右根
重点看“根”的位置,在最前面就是前序,中间就是中序,后面就是后序。补充一点,上述排列都是DFT(深度优先排列,Depth First Traversals)。另有Breadth First or Level Order Traversal 。
详解
首先上个例子:
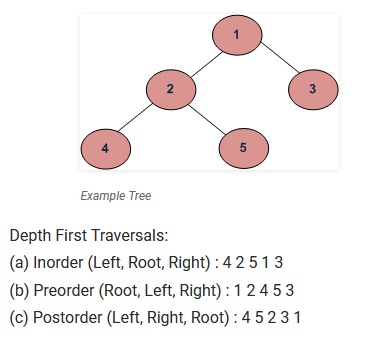
中序是左根右,所以从最左的左节点4开始(其他的还不够“左”,例如2,其实是4和5的根节点,所以不能从2开始),然后根节点2,然后右节点5,然后再上一层,把4、2、5看作一节点,那么1就是根节点,4、2、5是左节点,所以排列到1,最后右节点3。所以最后结果就如图所示,42513。
前序同理,首先根,所以从整棵树的根节点开始,因此到1,然后左节点,所以2,因为节点2是4和5的根节点,所以继续到4。4就是叶节点了,所以返回去,到右节点5……如此类推
C++中的实现
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
// 后序
void printPostorder(struct Node* node)
{
if (node == NULL)
return;
// first recur on left subtree
printPostorder(node->left);
// then recur on right subtree
printPostorder(node->right);
// now deal with the node
// 注意这行的位置,其实前中后序的实现组合是一样的,只是顺序不一样
cout << node->data << " ";
}
/* Given a binary tree, print its nodes in inorder*/
// 中序
void printInorder(struct Node* node)
{
if (node == NULL)
return;
/* first recur on left child */
printInorder(node->left);
/* then print the data of node */
cout << node->data << " ";
/* now recur on right child */
printInorder(node->right);
}
/* Given a binary tree, print its nodes in preorder*/
// 前序
void printPreorder(struct Node* node)
{
if (node == NULL)
return;
/* first print data of node */
cout << node->data << " ";
/* then recur on left sutree */
printPreorder(node->left);
/* now recur on right subtree */
printPreorder(node->right);
}
简单记忆方法:前序则对节点的操作在最前面(上例中为cout),其次是左右(递归)。相对应的,中序和后序分别就是在中间和后面。