SGU 253. Theodore Roosevelt 极角序+二分

/*
* 253. Theodore Roosevelt
* 题目：给出一个逆时针的凸包，然后再给出m个点，问这m个点是否至少有k个点在凸包里面
* （包括在边界上）
* 分析：O(n)的询问方式肯定TLE，所以我们可以像做动态凸包那种方式用set或者splay来维
* 护一个极角序，二分询问的那个点的极角，然后再用叉积判断即可。

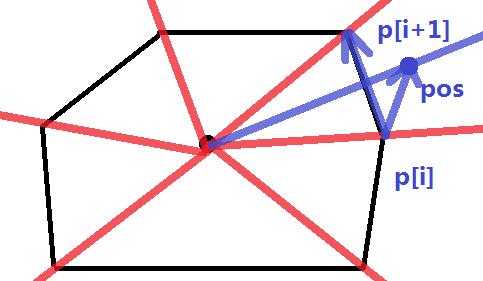
我们可以时刻用极角序维护一个凸包的点集。我们插入点pos的时候，我们可以计算出pos的极角，然后二分出pos的位置

（pos的极角恰好为p[i],p[i+1]中间）。然后判断叉积det(pos,p[i+1],p[i])是否新插入的点在凸包中。

*
* */

#include <cstdio>
#include <cstring>
#include <set>
#include <cmath>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const double eps = 1e-8;
const int X = 100005;

int dcmp(double x){
	if(fabs(x)<eps)
		return 0;
	return x>0?1:-1;
}

struct Point{
	ll x,y;
	double angle;
	Point(){}
	Point(ll _x,ll _y):x(_x),y(_y){}
	friend bool operator < (Point a,Point b){
		return dcmp(a.angle-b.angle)<0;
	}
	friend Point operator - (Point a,Point b){
		return Point(a.x-b.x,a.y-b.y);
	}
	void input(){
		scanf("%lld%lld",&x,&y);
		angle = atan2(y,x);
	}
};

set<Point> Convex;
int n,m,k;

ll det(Point a,Point b){
	return a.x*b.y-a.y*b.x;
}

ll det(Point a,Point b,Point o){
	return det(a-o , b-o);
}

Point Pre(Point pos){
	set<Point>::iterator it = Convex.lower_bound(pos);
	if(it==Convex.begin())
		return *(--Convex.end());
	return *(--it);
}

Point Next(Point pos){
	set<Point>::iterator it = Convex.upper_bound(pos);
	if(it==Convex.end())
		return *Convex.begin();
	return *it;
}

int cal(Point pos){
	Point pre = Pre(pos);
	Point next = Next(pre);
	return det(pre,next,pos)>=0;
}

int main(){
	//freopen("sumd.txt","r",stdin);
	cin>>n>>m>>k;
	Convex.clear();
	Point pos;
	for(int i=0;i<n;i++){
		pos.input();
		Convex.insert(pos);
	}
	int ans = 0;
	while(m--){
		pos.input();
		ans += cal(pos);
		if(ans>=k)
			break;
	}
	ans>=k?puts("YES"):puts("NO");

	return 0;
}