数据结构与算法（23）——表达式解析

• 树的应用：表达式解析

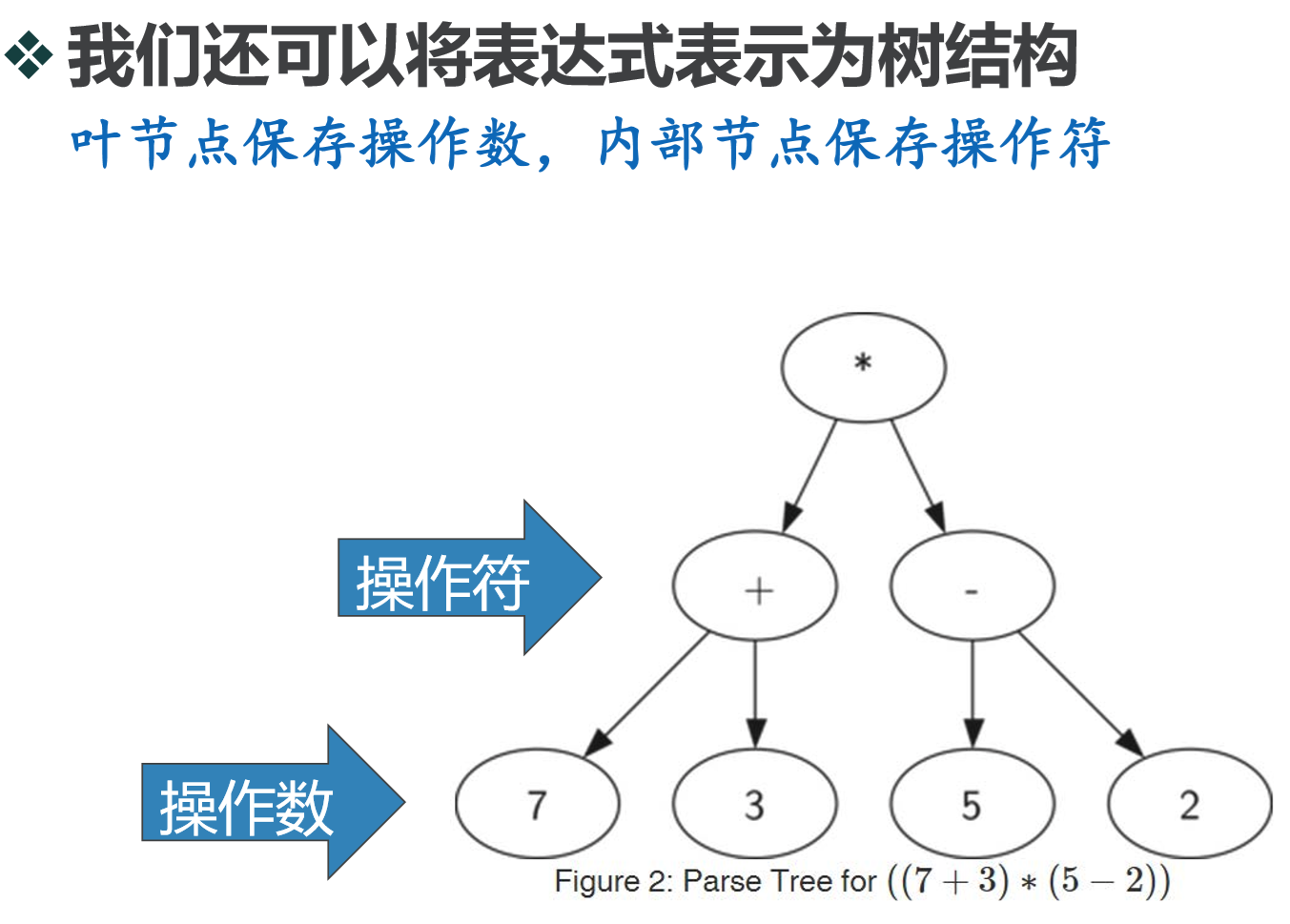
解析全括号表达式：(3+(4*5))

 

• 创建过程：

创建空树，当前节点为根节点

读入'('，创建了左子节点，当前节点下降

读入'3'，当前节点设置为3，上升到父节点

读入'+'，当前节点设置为+，创建右子节点，当前节点下降。

 读入'('，创建左子节点，当前节点下降

读入'4'，当前节点设置为4，上升到父节点

读入'*'，当前节点设置为*，创建右子节点，当 前节点下降

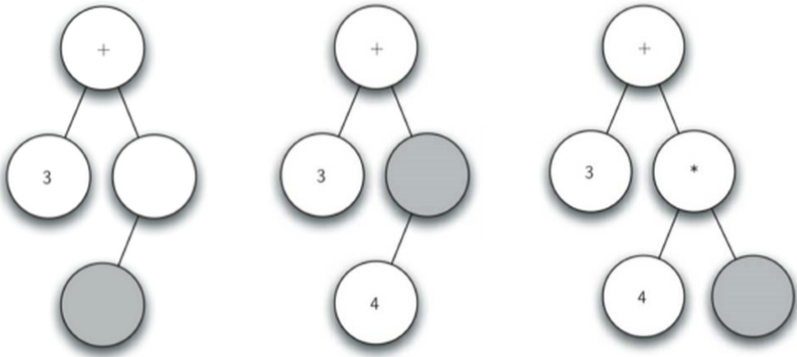
读入'5'，当前节点设置为5，上升到父节点

读入')'，上升到父节点

读入')'，再上升到父节点

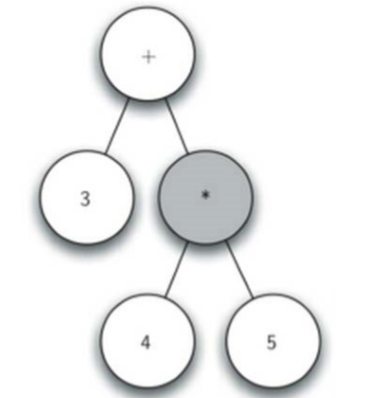
 总结下：如果当前单词是"("：为当前节点添加一个新节 点作为其左子节点，当前节点下降为这个新节点 如果当前单词是操作符"+,-,/,*"：将当前节点 的值设为此符号，为当前节点添加一个新节点作 为其右子节点，当前节点下降为这个新节点 如果当前单词是操作数：将当前节点的值设为此 数，当前节点上升到父节点 如果当前单词是")"：则当前节点上升到父节点。

 创建左右子树可调用insertLeft/Right

当前节点设置值，可以调用setRootVal

下降到左右子树可调用getLeft/RightChild 

创建一个栈来跟踪父节点：当前节点下降时，将下降前的节点push入栈 当前节点需要上升到父节点时，上升到pop出栈的节点即可！

from Stack import Stack
from Binary_Tree import BinaryTree
def buildParseTree(fpexp):
    fplist = fpexp.split()
    pStack = Stack()
    eTree = BinaryTree('') #创建一个空树
    pStack.push(eTree)
    currentTree = eTree
    for i in fplist:
        if i == "(":
            currentTree.insertLeft('')
            pStack.push(currentTree) #将老的当前节点入栈下降
            currentTree = currentTree.getLeftChild()
        elif i not in ['+', '-', '*', '/', ')']:
            currentTree.setRootVal(int(i)) #设置当前节点的值，为操作数
            parent = pStack.pop() #出栈上升
            currentTree = parent  #上升
        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i) #将当前阶段设置成操作符
            currentTree.insertRight('') #创建右子树
            pStack.push(currentTree) #把老的当前节点push到栈中
            currentTree = currentTree.getRightChild()
        elif i == ")":
            currentTree = pStack.pop()
        else:
            raise ValueError
    return eTree
flist = buildParseTree('( 3 + ( 4 * 5 ) )')

• 利用表达式解析树求值

创建了表达式解析树，可用来进行求值。由于二叉树BinaryTree是一个递归数据 结构，自然可以用递归算法来处理。由前述对子表达式的描述，可从树的底层子树开 始，逐步向上层求值，最终得到整个表达式的值。

求值函数evaluate的递归三要素：

基本结束条件：叶节点是最简单的子树，没有左 右子节点，其根节点的数据项即为子表达式树的值

缩小规模：将表达式树分为左子树、右子树，即为缩小规模

调用自身：分别调用evaluate计算左子树和右 子树的值，然后将左右子树的值依根节点的操作 符进行计算，从而得到表达式的值

这里引用函数引用包 operator。

from Stack import Stack
from Binary_Tree import BinaryTree
def buildParseTree(fpexp):
    fplist = fpexp.split()
    pStack = Stack()
    eTree = BinaryTree('') #创建一个空树
    pStack.push(eTree)
    currentTree = eTree
    for i in fplist:
        if i == "(":
            currentTree.insertLeft('')
            pStack.push(currentTree) #将老的当前节点入栈下降
            currentTree = currentTree.getLeftChild()
        elif i not in ['+', '-', '*', '/', ')']:
            currentTree.setRootVal(int(i)) #设置当前节点的值，为操作数
            parent = pStack.pop() #出栈上升
            currentTree = parent  #上升
        elif i in ['+', '-', '*', '/']:
            currentTree.setRootVal(i) #将当前阶段设置成操作符
            currentTree.insertRight('') #创建右子树
            pStack.push(currentTree) #把老的当前节点push到栈中
            currentTree = currentTree.getRightChild()
        elif i == ")":
            currentTree = pStack.pop()
        else:
            raise ValueError
    return eTree
flist = buildParseTree('( 3 + ( 4 * 5 ) )')