前面讲的是比较排序算法,主要有冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序等。
非比较排序算法:计数排序,基数排序,桶排序。在一定条件下,它们的时间复杂度可以达到O(n)。
一、桶排序(Bucket Sort)
1.1 桶排序介绍
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排。
【算法描述和实现】
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
public class BucketSort { public static void bucketSort(int[] arr) { int max = Integer.MIN_VALUE; int min = Integer.MAX_VALUE; for (int i = 0; i < arr.length; i++) { max = Math.max(max, arr[i]); min = Math.min(min, arr[i]); } //桶数 int bucketNum = (max - min) / arr.length + 1; ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum); for (int i = 0; i < bucketNum; i++) { bucketArr.add(new ArrayList<Integer>()); } //将每个元素放入桶 for (int i = 0; i < arr.length; i++) { int num = (arr[i] - min) / (arr.length); bucketArr.get(num).add(arr[i]); } //对每个非空的桶排序,排序后顺便存入临时的List,则list中已经有序) List<Integer> temp = new ArrayList<>(); for (int i = 0; i < bucketArr.size(); i++) { if (bucketArr.get(i) != null) { Collections.sort(bucketArr.get(i)); temp.addAll(bucketArr.get(i)); } } // 将temp中的数据写入原数组 for (int i = 0; i < arr.length; i++) { arr[i] = temp.get(i); } } public static void main(String[] args) { int[] arr = {29, 25, 3, 49, 9, 37, 21, 43}; bucketSort(arr); System.out.println(Arrays.toString(arr)); } }
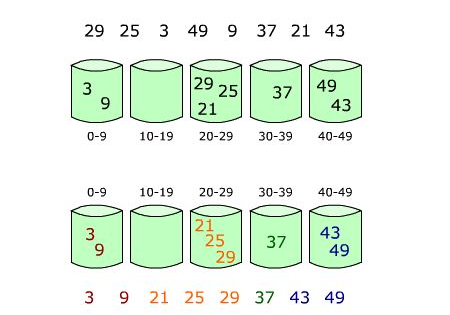
下图给出了对{ 29, 25, 3, 49, 9, 37, 21, 43 }进行桶排序的简单演示过程
【算法分析】
- 桶排序的时间复杂度通常是O(N+N*logM),其中,N表示桶的个数,M表示桶内元素的个数(这里,M取的是一个大概的平均数,这也说明,为何桶内的元素尽量不要出现有的很多,有的很少这种分布不均的事情,分布不均的话,算法的性能优势就不能最大发挥)。
- 桶排序可以是稳定的。这取决于我们对每个桶中的元素采取何种排序方法,比如桶内元素的排序使用快速排序,那么桶排序就是不稳定的;如果使用的是插入排序,桶排序就是稳定的。
- 桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。可以说其时间性能优势是由牺牲空间换来的。
1.2 桶排序经典应用(掌握)
【题目】
给定一个整型数组arr,返回排序后的相邻两数的最大差值 。
例如:
arr = [9, 3, 1, 10]。如果排序,结果为[1, 3, 9, 10],9和3的差为最大值,故返回6.
arr = [5, 5, 5, 5]。返回0.
要求时间复杂度O(N).
【基本思路】
如果用排序法实现,其时间复杂度为O(NlogN),而如果利用桶排序的思想(不是直接进行桶排序),可以做到时间复杂度O(N),空间复杂度O(N)。
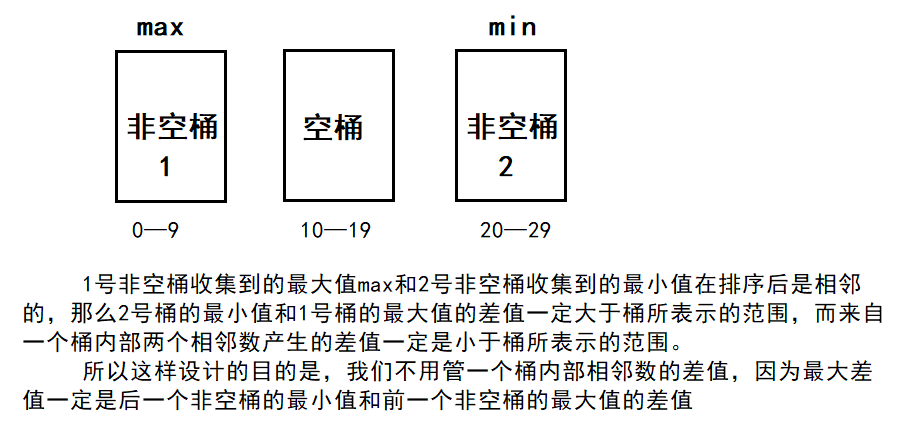
遍历数组arr,找到最大值max和最小值min。如果数组的长度为N,我们准备N+1个桶(0~N号桶),把最小值min放在第0号桶里,最大值max放在第N个桶里,那么中间的值放在哪个桶里呢?把min~max这个范围等分成N+1份,一个数属于哪个范围,就放在哪个桶里。举个例子:有一个长度为9的数组,最小值是0,最大值是99,那么就需要准备10个桶,0号桶的范围是0~9,1号桶的范围是10~19...9号桶的范围是90~99。
arr中[min, max)范围上的数放在0~N号桶里。对于0~N个桶,每个桶负责的区间大小为(max- min) / N。所以对于元素num,它应该被分配进的桶的编号是(num - min) / ((max - min) / N) = (num - min) * N / (max - min),注意:这里的桶的编号是从0开始计数的。
arr一共有N个数,其中min一定会放在0号桶,max一定会放在N号桶,所以如果把N个数放入N+1个桶,其中一定有桶是空的。那么差值最大的情况一定不来自同一个桶内的数。所以,如果arr经过排序,最大差值只可能来自某个非空桶的最小值减去前一个非空桶的最大值。每一个桶不用装所有进入里面的数,只用记录进入这个桶内的最小值和最大值(还要记录这个桶里面进没进来过数)
【代码实现】
public class MaxGap { public static int maxGap(int[] nums) { if (nums == null || nums.length < 2) { return 0; } int len = nums.length; int min = Integer.MAX_VALUE; int max = Integer.MIN_VALUE; //遍历数组,找到最小值和最大值 for (int i = 0; i < len; i++) { min = Math.min(min, nums[i]); max = Math.max(max, nums[i]); } if (min == max) { return 0; } /* 以下三个数组的目的:先把N+1号桶每一个桶的三组信息用3个数组来描述 */ //桶中是否有值 boolean[] hasNum = new boolean[len + 1]; //桶中的最大值 int[] maxs = new int[len + 1]; //桶中的最小值 int[] mins = new int[len + 1]; int bid = 0; for (int i = 0; i < len; i++) { //确定当前数属于几号桶 bid = bucket(nums[i], len, min, max); //更新桶中的最小值 mins[bid] = hasNum[bid] ? Math.min(mins[bid], nums[i]) : nums[i]; //更新桶中的最大值 maxs[bid] = hasNum[bid] ? Math.max(maxs[bid], nums[i]) : nums[i]; //这个数要去几号桶,这个桶的hasNum就改为true hasNum[bid] = true; } int res = 0; int lastMax = maxs[0]; int i = 1; //找到每一个非空桶和离它最近的左边的非空的桶,用当前的最小值减去前一个的最大值 for (; i <= len; i++) { if (hasNum[i]) { res = Math.max(res, mins[i] - lastMax); lastMax = maxs[i]; } } return res; } public static int bucket(long num, long len, long min, long max) { return (int) ((num - min) * len / (max - min)); } public static void main(String[] args) { int[] arr = {9, 3, 1, 10}; int max = maxGap(arr); System.out.println(max); } }
二、计数排序(Counting Sort)
计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况,它是一个非基于比较的排序算法,其空间复杂度和时间复杂度均为O(n+k),其中k是整数的范围,快于任何比较排序算法。当然这是一种牺牲空间换取时间的做法。
【基本思想】
对于给定的输入序列中的每一个元素x,确定该序列中值小于x的元素的个数(此处并非比较各元素的大小,而是通过对元素值的计数和计数值的累加来确定)。一旦有了这个信息,就可以将x直接存放到最终的输出序列的正确位置上。
文字说明比较抽象,先上图举例来分析一下其过程。
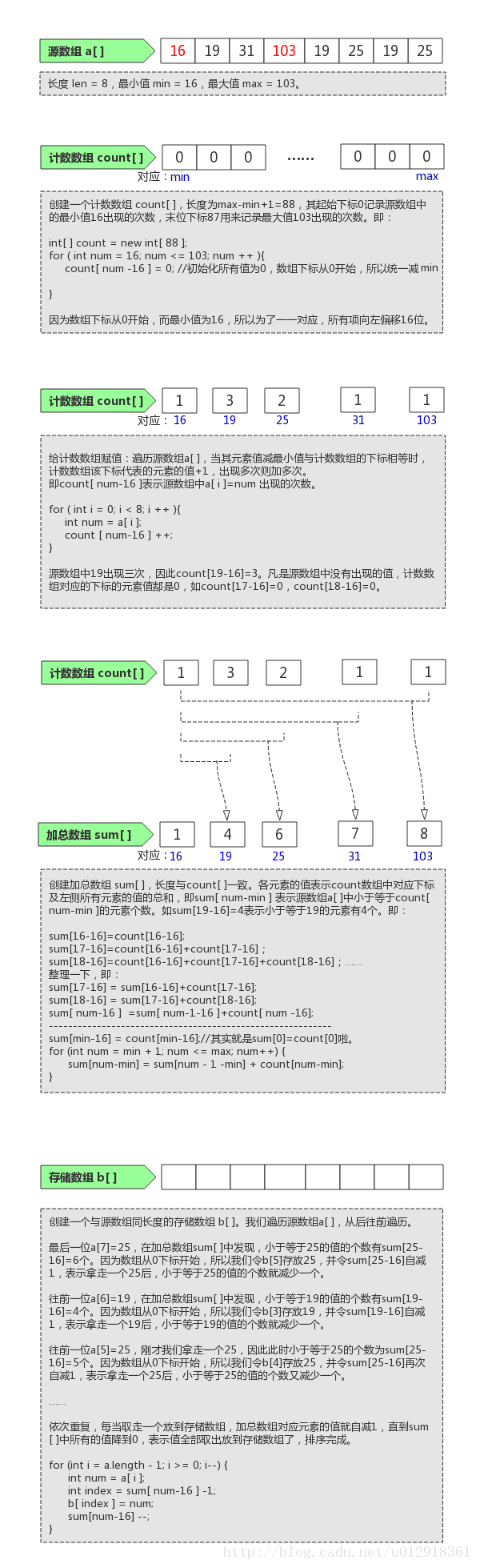
【图解说明】
根据图解过程发现,我们采用计数排序需要知道一些前提条件。例如数组中的最大值与最小值。所以写代码时,显然这个是需要作为形参手动传入的。
当然,也有人想,我何必用肉眼去观察呢,可以用其它排序手法写个程序找出其最大值最小值,再传入此处啊。认真思考一下,这样多没意思啊,其它排序手法直接就可以排好序啊,真这样做又何必多此一举再用计数排序呢。
所以,这里其实引申出了计数排序的使用场景。就是无论数列有多少元素,其最大值最小值应当容易辨别。例如高中生考试的总分数,显然用0-750就OK啦;又比如一群人的年龄,用个0-150应该就可以了,再不济就用0-200喽。
除了最值容易辨别外,还有个暗含条件是,最大值最小值不能相差太大,否则需要消耗很多的资源。例如数组{1,20000000,5,8},最大值最小值容易辨别,但!如果用计数排序,那么新建计数数组的长度是2千万,显然这种场景不应该采用计数排序。
【代码实现】
public class CountSort { public static void countSort(int[] a, int max, int min) { //存储数组 int[] b = new int[a.length]; //计数数组 int[] count = new int[max - min + 1]; //加总数组 int[] sum = new int[max - min + 1]; for (int num = min; num <= max; num++) { //初始化各元素值为0,数组下标从0开始因此减min count[num - min] = 0; } for (int i = 0; i < a.length; i++) { int num = a[i]; //每出现一个值,计数数组对应元素的值+1 count[num - min]++; } sum[0] = count[0]; for (int num = min + 1; num <= max; num++) { //加总数组元素的值为计数数组对应元素及左侧所有元素的值的总和 sum[num - min] = sum[num - min - 1] + count[num - min]; } for (int i = 0; i < a.length; i++) { //源数组第i位的值 int num = a[i]; //加总数组中对应元素的下标 int index = sum[num - min] - 1; //将该值存入存储数组对应下标中 b[index] = num; //加总数组中,该值的总和减少1。 sum[num - min]--; } for (int i = 0; i < a.length; i++) { //将存储数组的值一一替换给源数组 a[i] = b[i]; } } public static void main(String[] args) { int[] a = new int[]{6, -2, -8, 9, 3}; //9和-8分别是最大值和最小值。 countSort(a, 9, -8); System.out.println(Arrays.toString(a)); } }
三、基数排序(Radix Sort)
【算法简介】
基数排序是按照低位先排序,然后收集(就是按低位排序);再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
【算法描述和实现】
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);
public static void radixSort(int[] array, int maxDigit) { int len = array.length; int digitCount = 1; int digitDev = 1; int[] tmp = new int[len]; int[] count = new int[10]; while (digitCount <= maxDigit) { Arrays.fill(count, 0); Arrays.fill(count, 0); for (int i = 0; i < len; i++) { count[(array[i] / digitDev) % 10]++; } int sum = 0; for (int i = 1; i < 10; i++) { count[i] = count[i] + count[i - 1]; } for (int i = len - 1; i >= 0; i--) { tmp[count[(array[i] / digitDev) % 10] - 1] = array[i]; count[(array[i] / digitDev) % 10]--; } for (int i = 0; i < len; i++) { array[i] = tmp[i]; } digitDev *= 10; digitCount++; } }
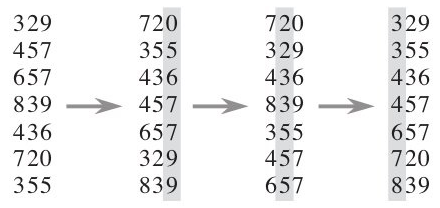
下图给出了对{ 329, 457, 657, 839, 436, 720, 355 }进行基数排序的简单演示过程
【算法分析】
最佳情况:T(n) = O(n * k)
最差情况:T(n) = O(n * k)
平均情况:T(n) = O(n * k)
基数排序 vs 计数排序 vs 桶排序
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
基数排序:根据键值的每位数字来分配桶
计数排序:每个桶只存储单一键值
桶排序:每个桶存储一定范围的数值
参考:https://www.cnblogs.com/xdyixia/p/9151938.html
https://blog.csdn.net/u012918361/article/details/70185637