50.Pow(x,n)

---

• 暴力解题绝对没救 ，肯定超时
• 本题通过使用快速幂来降低时间复杂度，而从解题思路上可分为 快速幂+递归 ，快速幂+迭代

快速幂 +递归

• 本题较为容易想到的是使用递归的方式

  • 以 计算Pow（2,35）为例 x=2，n=35；

  
  

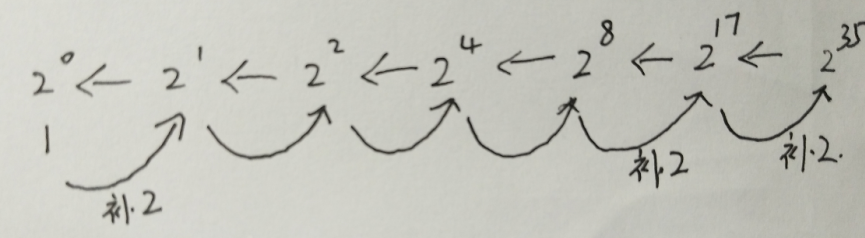
  • 由上图可知 （从右往左）指数35->17->8.....->0 通过 n/2 的方式一直拆分，即“递”操作
  • 递推的终止条件 为 n==0 此时返回1.0 设置 y 存储 中间值
  • 开始 “归” 操作 （从左往右）
    • 当N%2==1时（N为奇数） 需要在原来基础上(y*y) 补充x,即 (y*y*x)
    • 反之（N为偶数）直接（y*y）

  代码

     public double myPow(double x,int n){
          int N=n;
          return N>=0?quickMul(x, N):quickMul(x, -N);
      }
  
      public double quickMul(double x,int N){
          //递归结束条件
          if(N==0) return 1.0;
          double y=quickMul(x,N/2);
          return N%2==1?y*y*x:y*y;
      }
  

  • 时间复杂度O(log n) 即递归的次数
  • 空间复杂度O(log n) * 空间复杂度 O(log n) 递归的层数 这是由于递归的函数调用会使用栈空间

---

快速幂+迭代

• 据上述所知 递归方式 导致 空间占用率 受递归的次数的影响，极有可能导致栈溢出。可以采用迭代的方式进行空间优化

• 官方详解 妙。。。

  
  

代码

    /**
     * 快速幂+迭代
     */
    public double quickMul(double x, long N) {
        double ans = 1.0;
        // 贡献的初始值为 x
        double x_contribute = x;
        // 在对 N 进行二进制拆分的同时计算答案
        while (N > 0) {
            if (N % 2 == 1) {
                // 如果 N 二进制表示的最低位为 1，那么需要计入贡献
                ans *= x_contribute;
            }
            // 将贡献不断地平方
            x_contribute *= x_contribute;
            // 舍弃 N 二进制表示的最低位，这样我们每次只要判断最低位即可
            N /= 2;
        }
        return ans;
    }

• 很明显 空间复杂度 O(1)