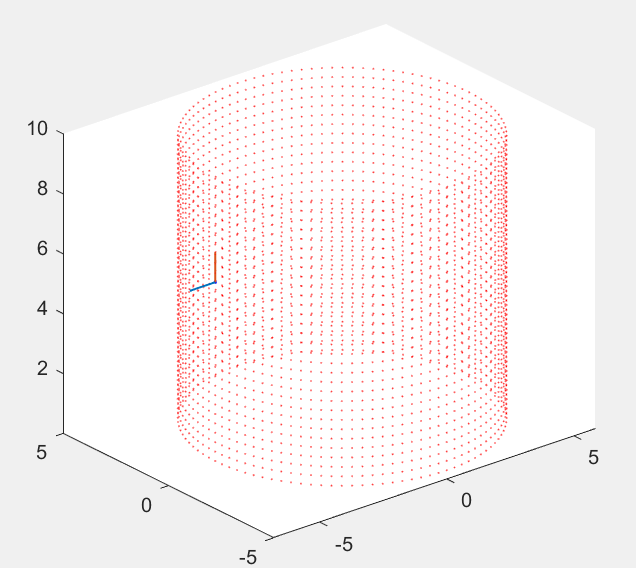
1.绘制圆柱体,计算圆柱体表面某一点的法向量。
1 r=5; 2 h=10; 3 n=100;%分点数 4 radius = 1.0;%搜索半径 5 min_neighbors = 8; 6 %------------------------------- 7 n_h= floor(h/(r*2*pi/n)); 8 X=zeros(n,n_h); 9 Y=zeros(n,n_h); 10 Z=zeros(n,n_h); 11 for j=1:n_h 12 for i=1:n 13 X(i,j)=r*cos(i*2*pi/n); 14 Y(i,j)=r*sin(i*2*pi/n); 15 Z(i,j)=j*r*2*pi/n; 16 end 17 end 18 19 data=zeros(n*n_h,3); 20 data(:,1)=reshape(X,[n*n_h,1]); 21 data(:,2)=reshape(Y,[n*n_h,1]); 22 data(:,3)=reshape(Z,[n*n_h,1]); 23 tree=KDTreeSearcher(data); 24 query=[X(50,20),Y(50,20),Z(50,20)]; 25 hold on 26 plot3(X,Y,Z,'r.','MarkerSize',1) 27 plot3(query(:,1),query(:,2),query(:,3),'b.','MarkerSize',4) 28 idx = rangesearch(tree, query, radius); 29 idxs = idx{1}; 30 neighbors = [data(idxs(:),1) data(idxs(:),2) data(idxs(:),3)]; 31 if size(neighbors) < min_neighbors 32 normal = {1}; 33 return; 34 end 35 C = cov(neighbors);% 计算协方差矩阵 36 [v, lambda] = eig(C); 37 [~, i_min] = min(diag(lambda)); 38 [~, i_max] = max(diag(lambda)); 39 normal = v(:,i_min) ./ norm(v(:,i_min)); 40 normal_max = v(:,i_max) ./ norm(v(:,i_max)); 41 query1=[normal(1,1)+ query(1,1),normal(2,1)+ query(1,2),normal(3,1)+ query(1,3)]; 42 query2=[normal_max(1,1)+ query(1,1),normal_max(2,1)+ query(1,2),normal_max(3,1)+ query(1,3)]; 43 plot3([query1(1,1) query(1,1)],[query1(1,2) query(1,2)],[query1(1,3) query(1,3)],'LineWidth',1); 44 plot3([query2(1,1) query(1,1)],[query2(1,2) query(1,2)],[query2(1,3) query(1,3)],'LineWidth',1); 45 46 47 hold off 48 axis equal