三次样条插值

三次样条插值函数：

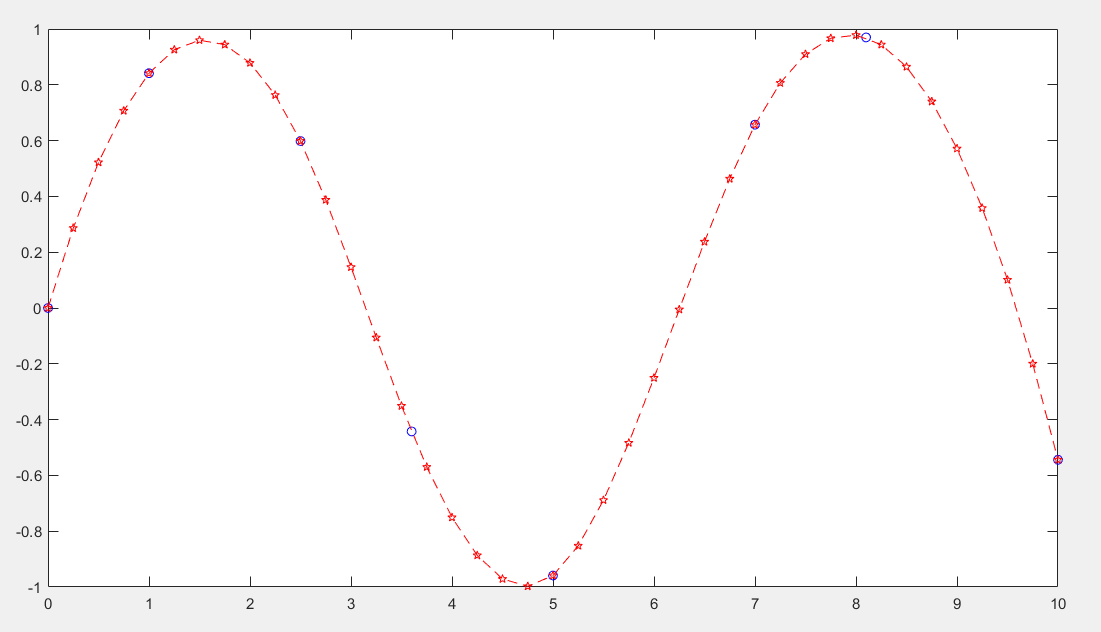
被插值函数：f(x)=1/(1+x^2)    -5<=x<=5

插值点-5，-4，-3，-2，-1,0,1,2,3,4,5

clc;clear;
x=-5:5;
y=1./(1+x.^2);
figure(1);hold on;plot(x,y,'r-o');
xi=-5:.05:5;
yi=spline(x,y,xi);
plot(xi,yi,'b-o');

官方文档：

https://ww2.mathworks.cn/help/matlab/ref/spline.html

语法

s = spline(x,y,xq)

pp = spline(x,y)

 

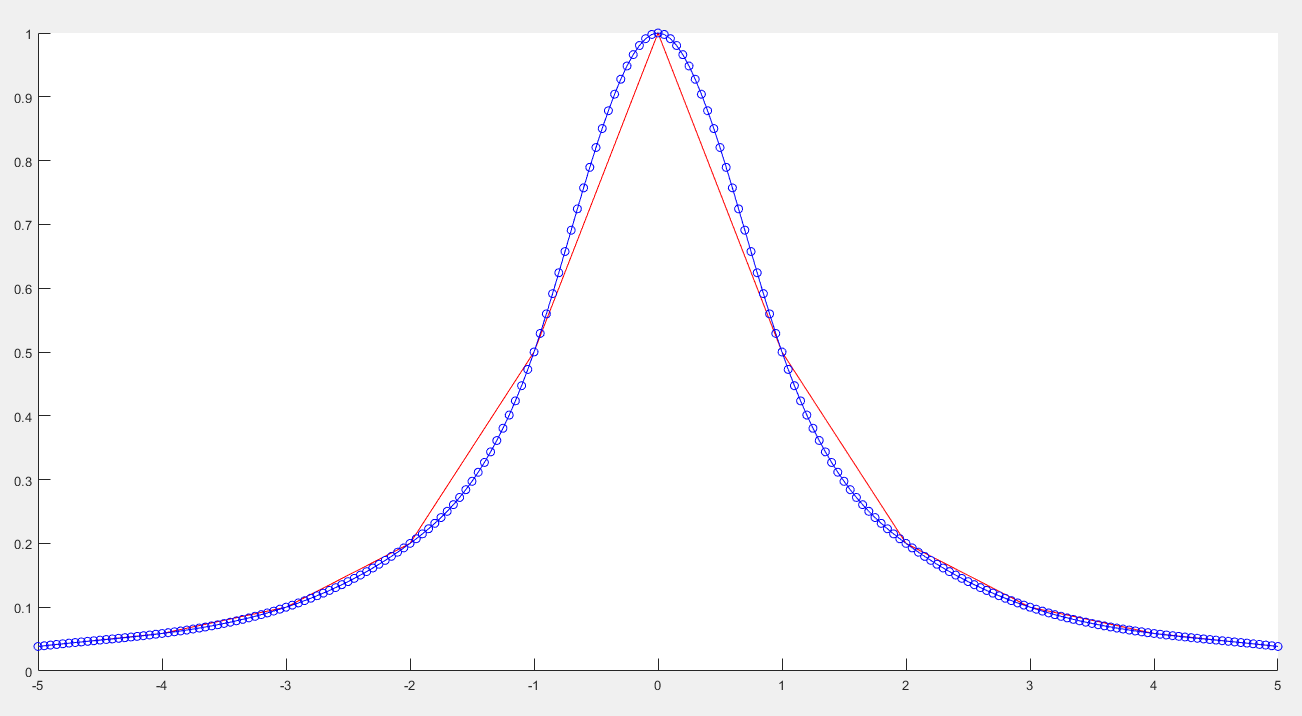
说明

s = spline(x,y,xq) 返回与 xq 中的查询点对应的插值 s 向量。s 的值由 x 和 y 的三次样条插值函数确定。

pp = spline(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。

例1

正弦数据的样条插值

使用 spline 基于非均匀分布的样本点对正弦曲线插值。

clc;clear;
x = [0 1 2.5 3.6 5 7 8.1 10];
y = sin(x);
xx = 0:.25:10;
yy = spline(x,y,xx);
plot(x,y,'bo',xx,yy,'rp--')

注：蓝色圆圈是插值点，红色五角星是点带入插值函数后的结果。

例2

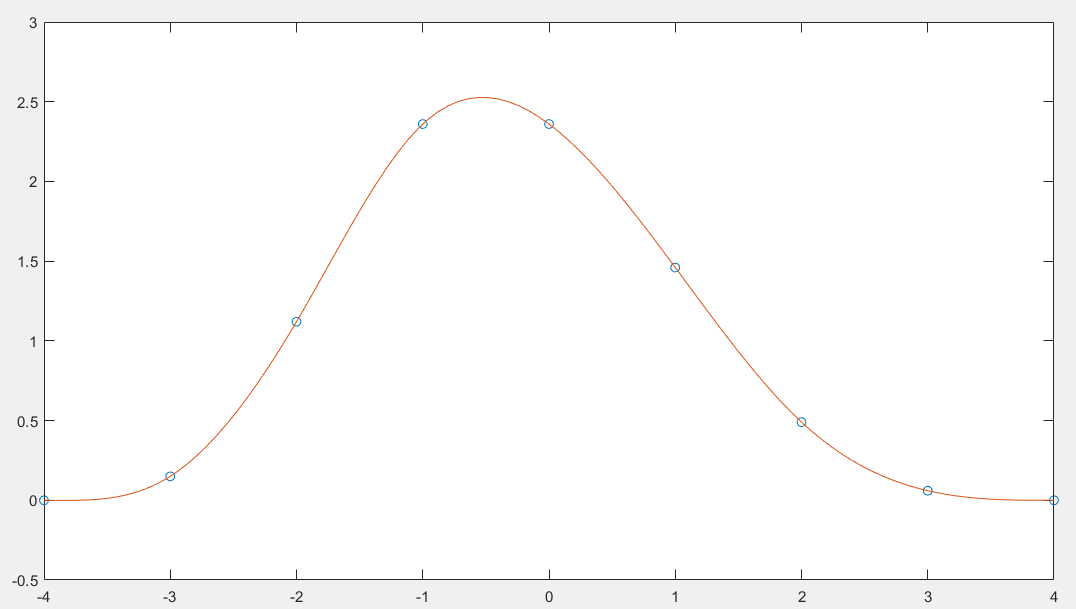
具有指定端点斜率的分布的样条插值

当端点斜率已知时，使用 clamped 或 complete 样条插值。此示例在插值的终点处强制实施零斜率。

x = -4:4;
y = [0 .15 1.12 2.36 2.36 1.46 .49 .06 0];
cs = spline(x,[0 y 0]);
xx = linspace(-4,4,101);
plot(x,y,'o',xx,ppval(cs,xx),'-');

注：

cs = spline(x,[0 y 0]);%这一句注明了插值点坐标和第一类边界条件，即提供端点处的一阶导数值。

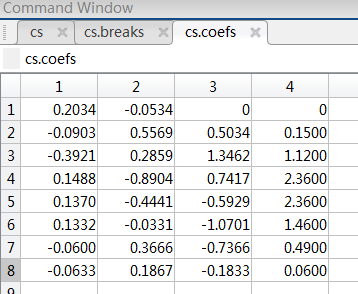
 返回的插值结果是一个结构体，

 

cs.coefs是每一段插值函数的系数，9个插值点，共8段样条函数，每个样条函数有4个系数。