随机梯度下降

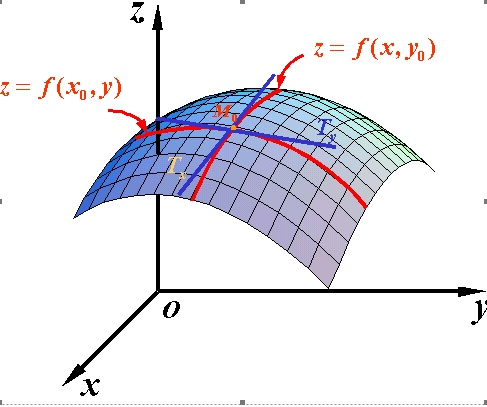
理解随机梯度下降，首先要知道梯度下降法，故先介绍梯度下降法：

梯度下降法

大多数机器学习或者深度学习算法都涉及某种形式的优化。 优化指的是改变 以最小化或最大化某个函数 的任务。 我们通常以最小化 指代大多数最优化问题。 最大化可经由最小化算法最小化 来实现。

我们把要最小化或最大化的函数称为目标函数或准则。 当我们对其进行最小化时，我们也把它称为代价函数、损失函数或误差函数。

下面，我们假设一个损失函数为

其中 然后要使得最小化它。

注意：这里只是假设，不用知道这个目标函数就是平方损失函数等等，然后肯定有人问既然要最小化它，那求个导数，然后使得导数等于0求出不就好了吗？是的，有这样的解法，可以去了解正规方程组求解。说下这里不讲的原因，主要是那样的方式太难求解，然后在高维的时候，可能不可解，但机器学习或深度学习中，很多都是超高维的，所以也一般不用那种方法。总之，梯度下降是另一种优化的不错方式，比直接求导好很多。

梯度下降：

先说一下梯度：

 图片来源：https://www.zhihu.com/question/36301367/answer/142096153

1.梯度是在某一点处z对x的偏导与z对y的偏导的矢量和；

2.梯度是一个矢量，既有大小，又有方向；

3.梯度总是指向z值增长最大（快）的方向，矢量和的大小表示这个方向上增加的量，矢量和的方向表示梯度的方向。

我们知道曲面上方向导数的最大值的方向就代表了梯度的方向，因此我们在做梯度下降的时候，应该是沿着梯度的反方向进行权重的更新，可以有效的找到全局的最优解。这个 的更新过程可以描述为

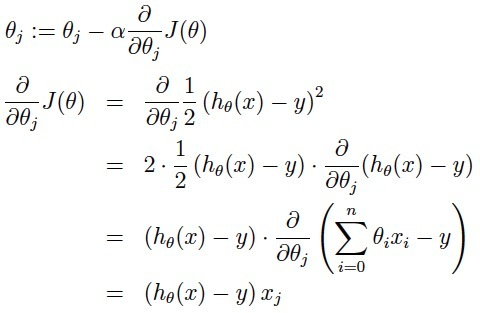
a表示的是步长或者说是学习率（learning rate），决定着梯度下降的步长。

从数学的角度，我们可以这样想，先想在低维的时候，比如二维，我们要找到最小值，其实可以是这样的方法，具体化到1元函数中时，梯度方向首先是沿着曲线的切线的，然后取切线向上增长的方向为梯度方向，2元或者多元函数中，梯度向量为函数值f对每个变量的导数，该向量的方向就是梯度的方向，当然向量的大小也就是梯度的大小。现在假设我们要求函数的最值，采用梯度下降法，结合如图所示：

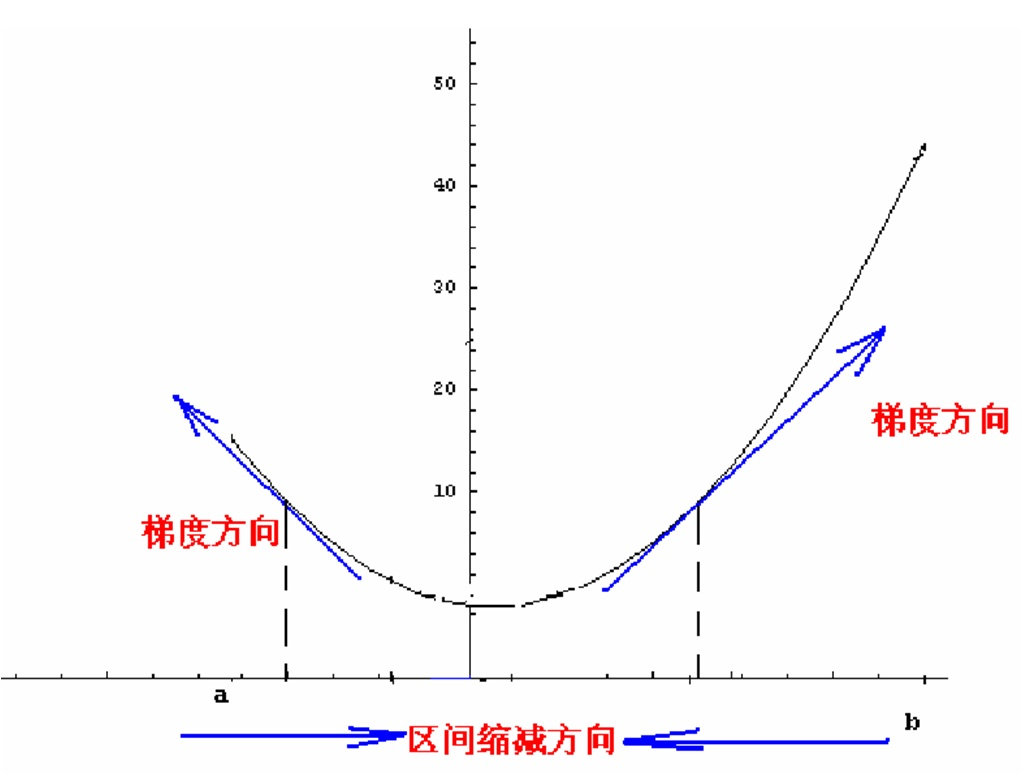
如图所示，我们假设函数是 ,那么如何使得这个函数达到最小值呢，简单的理解，就是对x求导，得到 y'=2x ，然后用梯度下降的方式，如果初始值是（0的左边）负值,那么这是导数也是负值，用梯度下降的公式，使得x更加的靠近0,如果是正值的时候同理。注意：这里的梯度也就是一元函数的导数，高维的可以直接类推之

来源：https://www.zhihu.com/question/264189719/answer/291167114

 

---

 以上是分割线。

总样本数=10000（张桌子）

每个 batch 都从 10000 个样本里随机采样 10 个，然后计算、更新，再随机采样 10 个，再一个 batch 。。。这里的更新，叫随机梯度下降，随机是指你每个 batch 的数据是对整个数据空间的随机采样。

随机梯度下降的理论（其实算不上理论。。。很直观的一个式子）告诉你，只要你的采样够随机，随机梯度的期望和真实梯度是相等的。用人话说，放在模型训练里，哪怕一个 batch 就一个数据点，你只要辛苦多迭代几个 batch，最终效果一定是一样的。

---

函数梯度：导数dy/dx的多变量表达式，用来表示y相对于x的瞬时变化率。往往为了计算多变量函数的导数时，会用梯度取代导数，并使用偏导数来计算梯度。梯度和导数之间的一个主要区别是函数的梯度形成了一个向量场。

因此，对单变量函数，使用导数来分析；而梯度是基于多变量函数而产生的。

---

1. 随机梯度下降(SDG)

随机梯度下降（Stochastic gradient descent，SGD）对每个训练样本进行参数更新，每次执行都进行一次更新，且执行速度更快。

θ=θ−η⋅∇(θ) × J(θ;x(i);y(i))，其中x(i)和y(i)为训练样本。

频繁的更新使得参数间具有高方差，损失函数会以不同的强度波动。这实际上是一件好事，因为它有助于我们发现新的和可能更优的局部最小值，而标准梯度下降将只会收敛到某个局部最优值。

但SGD的问题是，由于频繁的更新和波动，最终将收敛到最小限度，并会因波动频繁存在超调量。

虽然已经表明，当缓慢降低学习率η时，标准梯度下降的收敛模式与SGD的模式相同。

图2：每个训练样本中高方差的参数更新会导致损失函数大幅波动，因此我们可能无法获得给出损失函数的最小值。

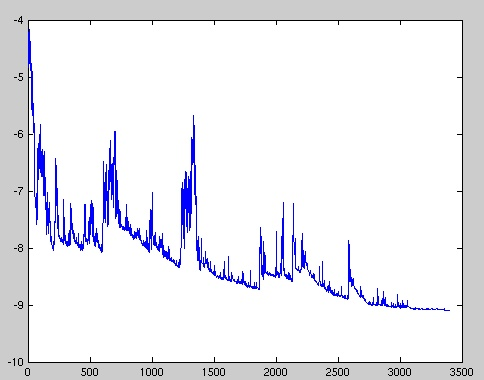
另一种称为“小批量梯度下降”的变体，则可以解决高方差的参数更新和不稳定收敛的问题。

2. 小批量梯度下降

为了避免SGD和标准梯度下降中存在的问题，一个改进方法为小批量梯度下降（Mini Batch Gradient Descent），因为对每个批次中的n个训练样本，这种方法只执行一次更新。

batch_sizebatch_size中的n通常设置为2的幂次方，通常设置2，4，8，16，32，64，128，256，5122，4，8，16，32，64，128，256，512（很少设置大于512）。因为设置成2的幂次方，更有利于GPU加速。

使用小批量梯度下降的优点是：

1) 可以减少参数更新的波动，最终得到效果更好和更稳定的收敛。

2) 还可以使用最新的深层学习库中通用的矩阵优化方法，使计算小批量数据的梯度更加高效。

3) 通常来说，小批量样本的大小范围是从50到256，可以根据实际问题而有所不同。

4) 在训练神经网络时，通常都会选择小批量梯度下降算法。

这种方法有时候还是被成为SGD。

---

如何直观形象的理解方向导数与梯度以及它们之间的关系？

---

 

 梯度下降优化算法

梯度下降基本框架是 Mini-batch Gradient Descent，对每一个mini-batch更新一次参数，每一个mini-batch包含事先设置好的batch size个数的样本。而经常提到的SGD(Stochastic gradient descent)，则是对每一个样本更新一次参数，现实中人们更多将 Mini-batch Gradient Descent也视为SGD而不加以区别。假设训练集中输入特征为，对应样本标签为 ，参数为 ，损失函数为 ，batch size为 ，学习率为 ， 表示梯度符号。训练时每吃进个样本，按如下公式更新一次参数，注意减号表示往负梯度方向更新参数。

为什么会有 呢？负梯度为我们指明了前进的方向，但是每次前进多远为宜呢？ 就是为了控制迈出步子的大小。步子小了，走得慢，还可能跨不出当前的小坑；步子大了，则容易跨过当前的坑而错过最优解。由于是凭经验预先设置，也许算是有些人提出的深度学习是炼金术的一个论据吧。

• Momentum

SGD without momentum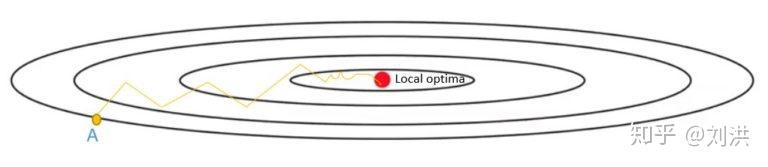SGD with momentum

如上图所示，黑色实现表示等高线，局部最优解在中间位置，中间横向位置存在沟壑。SGD在沿着沟壑探寻最优解时，由于维度众多，可能在某个维度的梯度分量比其他维度打很多，导致负梯度方向不是直接指向最优解，造成探寻轨迹在沟壑处左右徘徊，从而达到最优解颇费周折，训练时间拖慢。为优化此问题，momentum应运而生，字面意思是动量，即每次前行时，都考虑进上一步的梯度，与当前梯度一起决定这一步该如何走，如下式，其中 一般预设为0.9。

其实momentum更多是利用了惯性，如同一块石头从山顶滚到谷底。上一步负梯度与当前步负梯度方向相同时，会在该方向加速前行；上一步负梯度与当前步负梯度方向相反时，则抵消掉一些速度。如此利用上一步负梯度对当前梯度进行修正，可以加快探寻速度，减少不必要的波折。

---