P6 第2讲 矩阵02

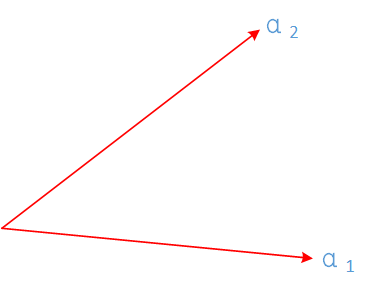
 如图：向量阿尔法1和阿尔法2既不是正交的向量，也都不是单位向量，它们两个线性无关。

 施密特标准正交化的过程如下(思路是不是正交的两个向量掰成正交)：

1. 任意找一个已给向量，记作贝塔1.如把阿尔法1记作贝塔1，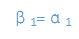

2. 对阿尔法2往阿尔法1投影.

 

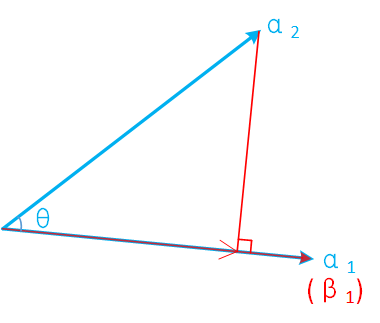
投影下来的向量长度是：||α2||cosθ

投影下来的向量是：||α2||cosθ再乘以一个方向，投影下来的方向和阿尔法1的方向相同，取阿尔法1的单位向量就行(单位向量是带方向的)，即：

 与阿尔法1正交的向量记作贝塔2，可以表示为：

 化简：

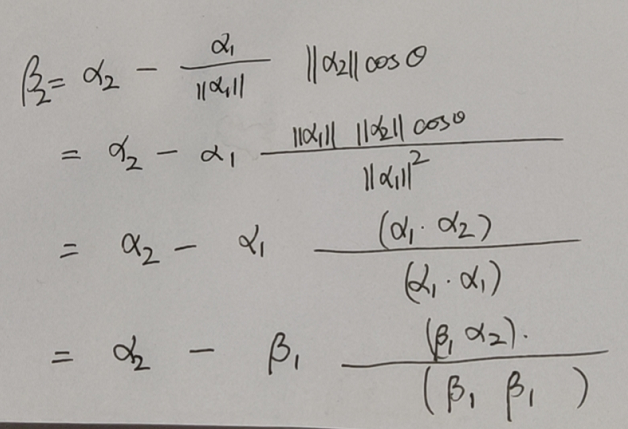
 再把贝塔1和贝塔2单位化，即可得到正交的单位向量组：

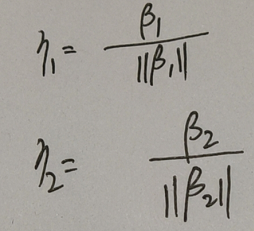
 以上就是施密特正交化的过程。

注解：

1. 线性无关的两个或者三个正交向量可以进行施密特标准正交化，进而化成像2维或者3维系中的坐标轴那样的正交单位向量组。 

 举例：

在计算单位向量ξ2的时候，不要直接对β1求平方和再开方，这样比较麻烦，可以先对它放大3倍，然后再求其单位向量，因为无论放大或者缩小几倍，求的单位向量都不会发生变化。

 注解：

• 标准(规范)正交向量组和标准(规范)正交基的名字的差别是：前者一般指互相垂直的单位向量，如果是3维的话，可以只包含2个；后者的话如果是2维则包含2个，如果是3维，则包含3个，它们分别能组成坐标轴的2个或者3个轴。即前者不限定个数，后者个数限定(个数等于维数的标准正交向量组)。

 (1)中的式子由于矩阵不满足交换律一般是不成立的，但(2)是成立的，因为不涉及到矩阵的交换律，只涉及到A的m次幂。

 注解：

• (9)的证明还是很复杂的。
• 对角阵极为重要。
• 对称矩阵也很重要(主对角线可以想象成是一面镜子)。

• 正交矩阵极为重要。

 注解：

• AA^T=E也能得出A^TA=E。

证明：

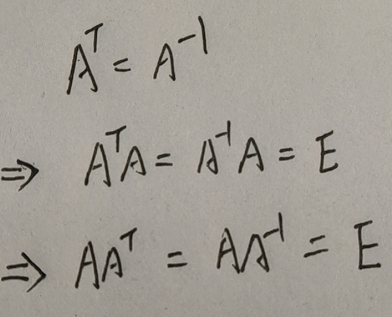
•  如果A(假如是3阶矩阵)是正交矩阵，则马上推出组成A的三个行都是单位向量，且两两正交。

 注解：

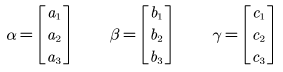
•  A是正交矩阵，则表明组成A的行向量组是规范正交基。
•  A是正交矩阵，则表明组成A的列向量组是规范正交基。
• 正交矩阵就是由规范正交基所拼成的矩阵。

 

 

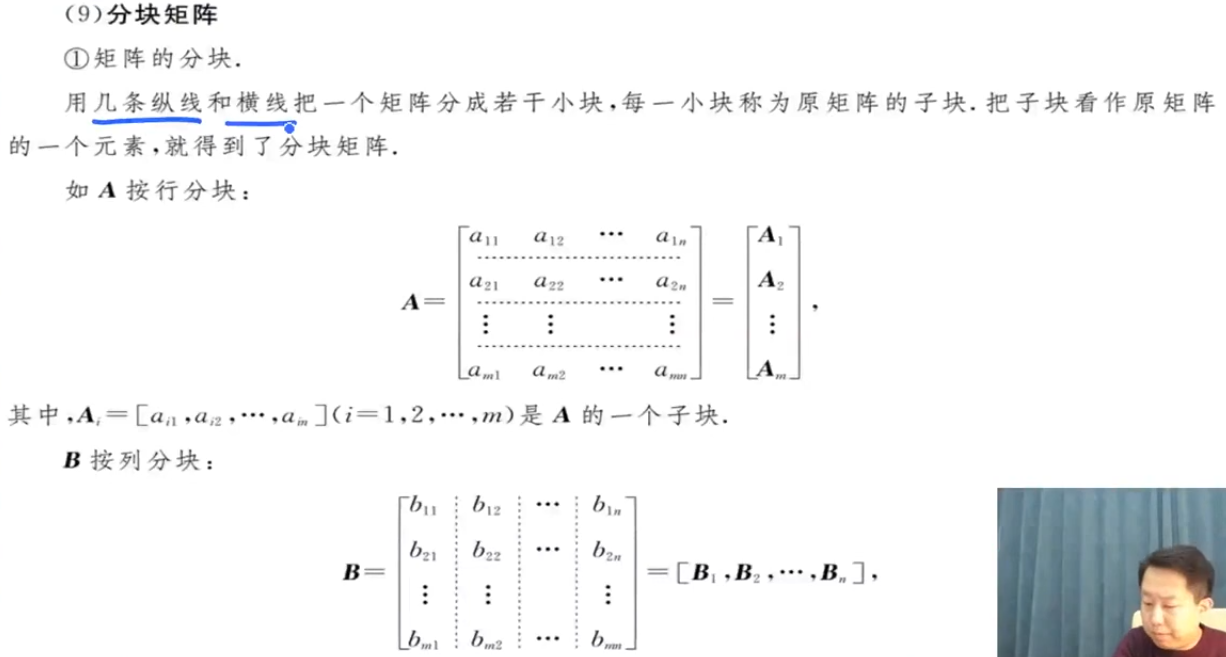
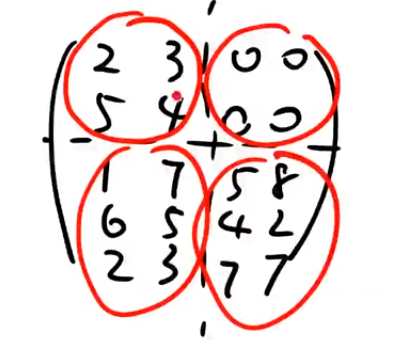
 注意：

 

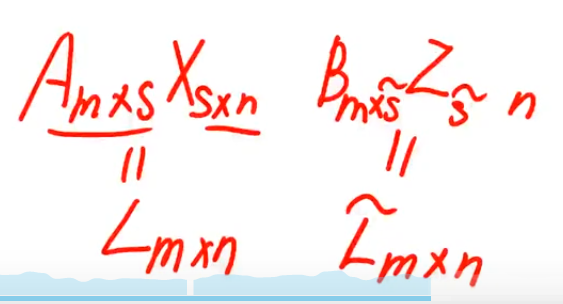
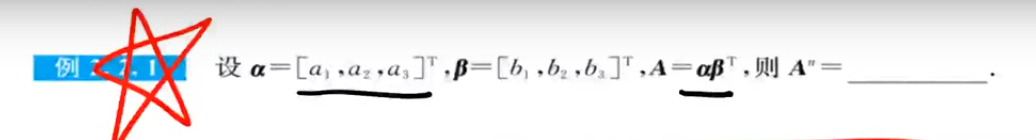
 注解：

• 给定一个矩阵，要学会倒着写。

 注解：

• 矩阵中一个向量能由其它两个向量线性表示，则此矩阵的秩是1.秩的定义就是：矩阵中最大线性无关组的向量的个数。
• 一阶子式不为0，所有超过1阶的子式都为0，所以R=1.

 

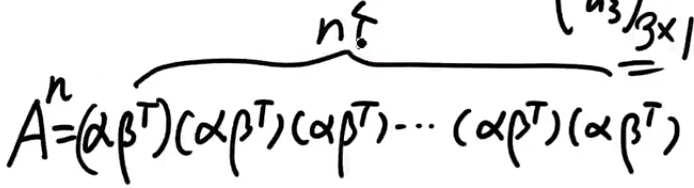
 矩阵的乘法没有交换律但是有结合律。i.e., ABC=(AB)C=A(BC)。

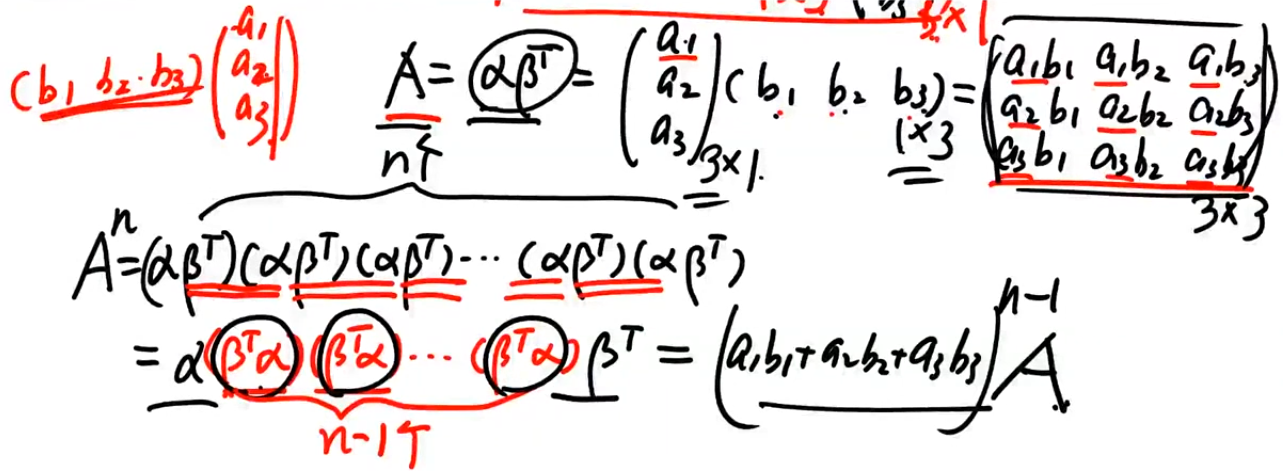
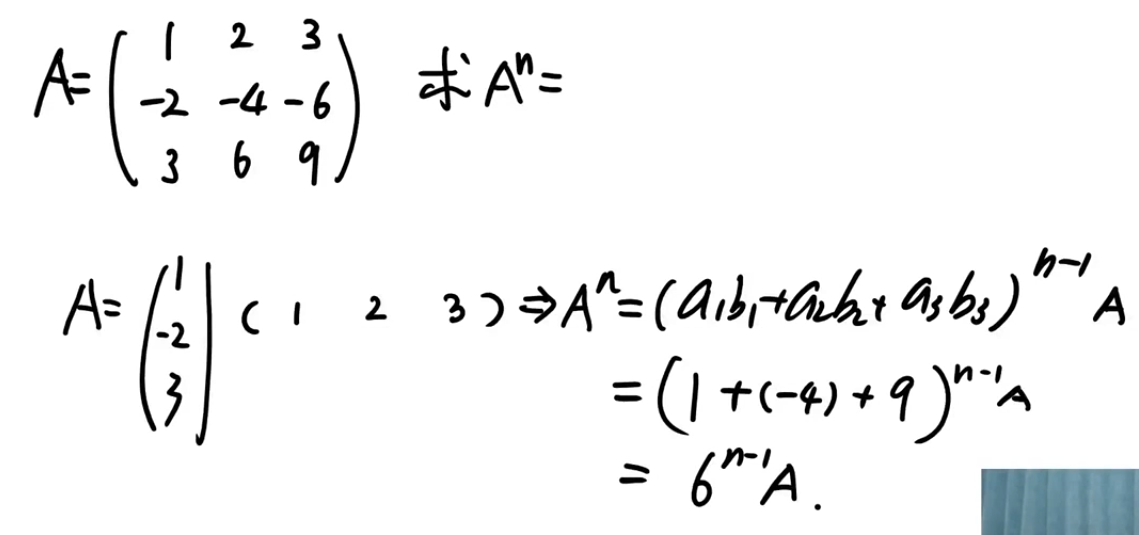
这种单行成比例秩为1的矩阵的n次方结果是主对角线元素的和的(n-1)次方，即矩阵的迹的(n-1)次方乘以矩阵本身，这个是偶然的吗？答：这个不是偶然，这是必然。

 

 

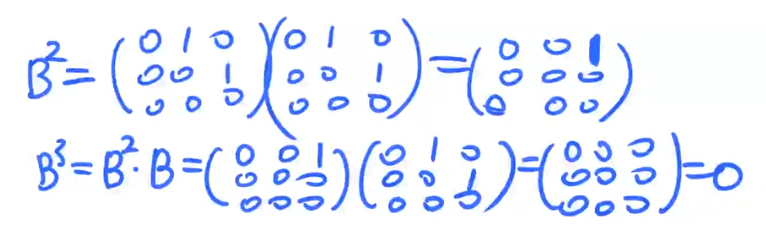
 注解：

1. B的3次方是0，那么B的比3次幂大的次幂都会为0.所以上面的二项式展开只写3项就行了 

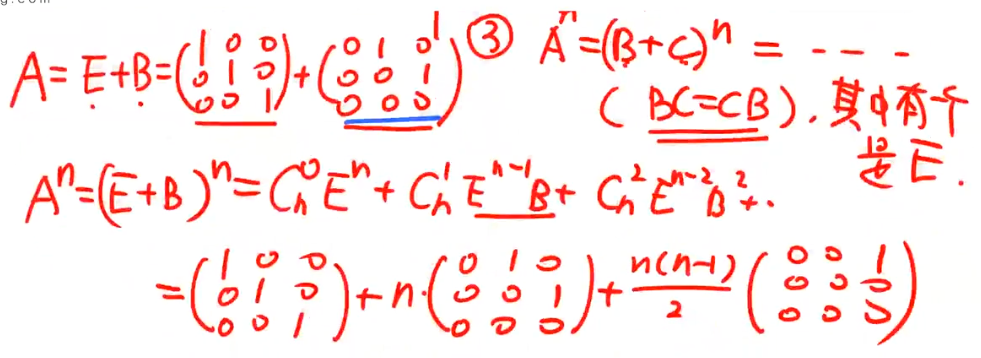
例题：

 

注解：

1. 因为β0的方向不确定，所以答案要添加一个正负号。

 

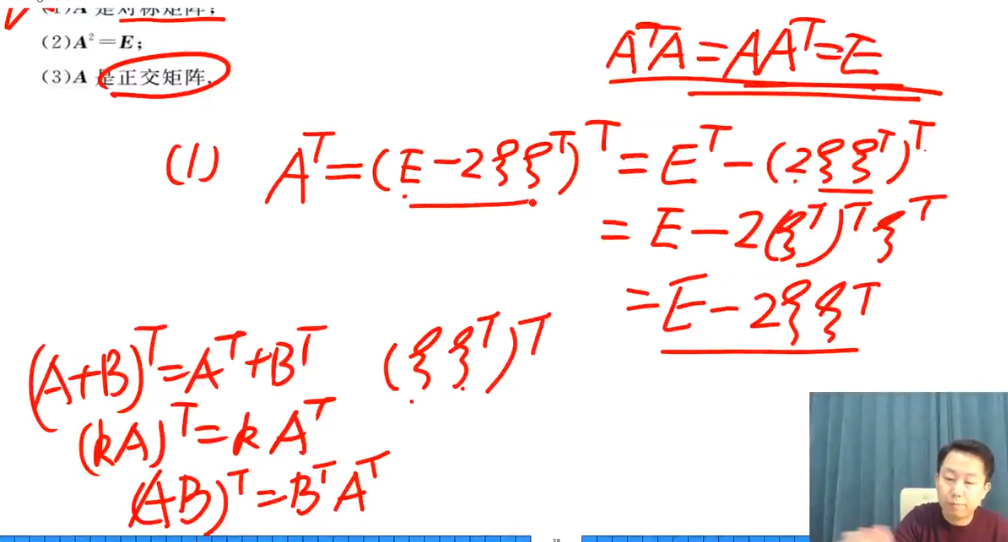
第二问：

 第3问：