算法介绍
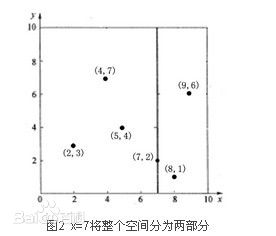
KD树的全称为k-Dimension Tree的简称,是一种分割K维空间的数据结构,主要应用于关键信息的搜索。为什么说是K维的呢,因为这时候的空间不仅仅是2维度的,他可能是3维,4维度的或者是更多。我们举个例子,如果是二维的空间,对于其中的空间进行分割的就是一条条的分割线,比如说下面这个样子。
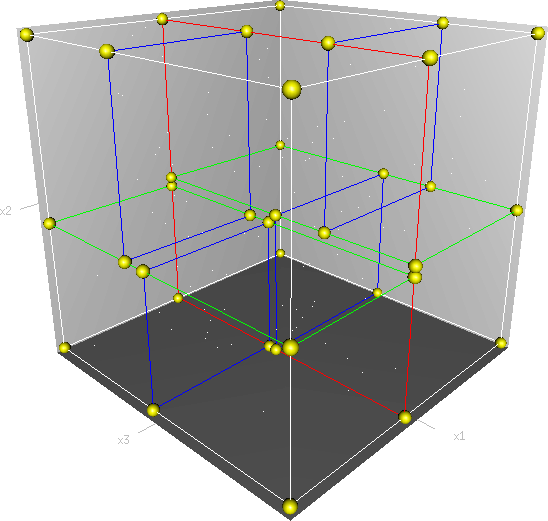
如果是3维的呢,那么分割的媒介就是一个平面了,下面是3维空间的分割
这就稍稍有点抽象了,如果是3维以上,我们把这样的分割媒介可以统统叫做超平面 。那么KD树算法有什么特别之处呢,还有他与K-NN算法之间又有什么关系呢,这将是下面所将要描述的。
KNN
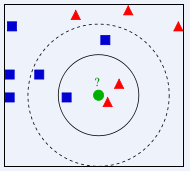
KNN就是K最近邻算法,他是一个分类算法,因为算法简单,分类效果也还不错,也被许多人使用着,算法的原理就是选出与给定数据最近的k个数据,然后根据k个数据中占比最多的分类作为测试数据的最终分类。图示如下:
算法固然简单,但是其中通过逐个去比较的办法求得最近的k个数据点,效率太低,时间复杂度会随着训练数据数量的增多而线性增长。于是就需要一种更加高效快速的办法来找到所给查询点的最近邻,而KD树就是其中的一种行之有效的办法。但是不管是KNN算法还是KD树算法,他们都属于相似性查询中的K近邻查询的范畴。在相似性查询算法中还有一类查询是范围查询,就是给定距离阈值和查询点,dbscan算法可以说是一种范围查询,基于给定点进行局部密度范围的搜索。想要了解KNN算法或者是Dbscan算法的可以点击我的K-最近邻算法和Dbscan基于密度的聚类算法。
KD-Tree
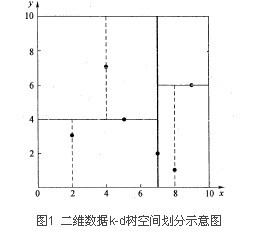
在KNN算法中,针对查询点数据的查找采用的是线性扫描的方法,说白了就是暴力比较,KD树在这方面用了二分划分的思想,将数据进行逐层空间上的划分,大大的提高了查询的速度,可以理解为一个变形的二分搜索时间,只不过这个适用到了多维空间的层次上。下面是二维空间的情况下,数据的划分结果:
现在看到的图在逻辑上的意思就是一棵完整的二叉树,虚线上的点是叶子节点。
KD树的算法原理
KD树的算法的实现原理并不是那么好理解,主要分为树的构建和基于KD树进行最近邻的查询2个过程,后者比前者更加复杂。当然,要想实现最近点的查询,首先我们得先理解KD树的构建过程。下面是KD树节点的定义,摘自百度百科:
|
域名
|
数据类型
|
描述
|
|
Node-data
|
数据矢量
|
数据集中某个数据点,是n维矢量(这里也就是k维)
|
|
Range
|
空间矢量
|
该节点所代表的空间范围
|
|
split
|
整数
|
垂直于分割超平面的方向轴序号
|
|
Left
|
k-d树
|
由位于该节点分割超平面左子空间内所有数据点所构成的k-d树
|
|
Right
|
k-d树
|
由位于该节点分割超平面右子空间内所有数据点所构成的k-d树
|
|
parent
|
k-d树
|
父节点
|
变量还是有点多的,节点中有孩子节点和父亲节点,所以必然会用到递归。KD树的构建算法过程如下(这里假设构建的是2维KD树,简单易懂,后续同上):
1、首先将数据节点坐标中的X坐标和Y坐标进行方差计算,选出其中方差大的,作为分割线的方向,就是接下来将要创建点的split值。
2、将上面的数据点按照分割方向的维度进行排序,选出其中的中位数的点作为数据矢量,就是要分割的分割点。
3、同时进行空间矢量的再次划分,要在父亲节点的空间范围内再进行子分割,就是Range变量,不理解的话,可以阅读我的代码加以理解。
4、对剩余的节点进行左侧空间和右侧空间的分割,进行左孩子和右孩子节点的分割。
5、分割的终点是最终只剩下1个数据点或一侧没有数据点的情况。
在这里举个例子,给定6个数据点:
(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)
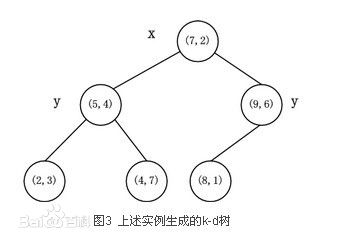
对这6个数据点进行最终的KD树的构建效果图如下,左边是实际分割效果,右边是所构成的KD树:
x,y代表的是当前节点的分割方向。读者可以进行手动计算并验证,本人不再加以描述。
KD树构建完毕,之后就是对于给定查询点数据,进行此空间数据的最近数据点,大致过程如下:
1、从根节点开始,从上往下,根据分割方向,在对应维度的坐标点上,进行树的顺序查找,比如给定(3,1),首先来到(7,2),因为根节点的划分方向为X,因此只比较X坐标的划分,因为3<7,所以往左边走,后续的节点同样的道理,最终到达叶子节点为止。
2、当然以这种方式找到的点并不一定是最近的,也许在父节点的另外一个空间内存在更近的点呢,或者说另外一种情况,当前的叶子节点的父亲节点比叶子节点离查询点更近呢,这也是有可能的。
3、所以这个过程会有回溯的步骤,回溯到父节点时候,需要做2点,第一要和父节点比,谁里查询点更近,如果父节点更近,则更改当前找到的最近点,第二以查询点为圆心,当前查询点与最近点的距离为半径画个圆,判断是否与父节点的分割线是否相交,如果相交,则说明有存在父节点另外的孩子空间存在于查询距离更短的点,然后进行父节点空间的又一次深度优先遍历。在局部的遍历查找完毕,在于当前的最近点做比较,比较完之后,继续往上回溯。
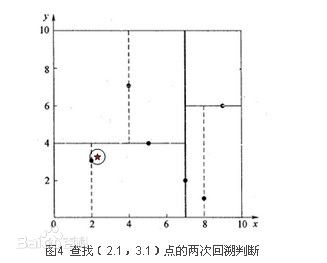
下面给出基于上面例子的2个测试例子,查询点为(2.1,3.1)和(2,4.5),前者的例子用于理解一般过程,后面的测试点真正诠释了递归,回溯的过程。先看下(2.1,3.1)的情况:
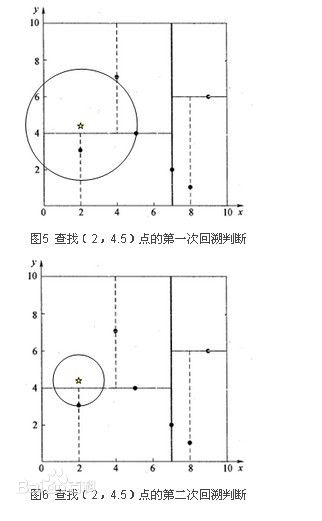
因为没有碰到任何的父节点分割边界,所以就一直回溯到根节点,最近的节点就是叶子节点(2,3).下面(2,4.5)是需要重点理解的例子,中间出现了一次回溯,和一次再搜索:
在第一次回溯的时候,发现与y=4碰撞到了,进行了又一次的搜寻,结果发现存在更近的点,因此结果变化了,具体的过程可以详细查看百度百科-kd树对这个例子的描述。
算法的代码实现
许多资料都是只有理论,没有实践,本人基于上面的测试例子,自己写了一个,效果还行,基本上实现了上述的过程,不过貌似Range这个变量没有表现出用途来,可以我一番设计,例子完全是上面的例子,输入数据就不放出来了,就是给定的6个坐标点。
坐标点类Point.java:
package DataMining_KDTree;
/**
* 坐标点类
*
* @author lyq
*
*/
public class Point{
// 坐标点横坐标
Double x;
// 坐标点纵坐标
Double y;
public Point(double x, double y){
this.x = x;
this.y = y;
}
public Point(String x, String y) {
this.x = (Double.parseDouble(x));
this.y = (Double.parseDouble(y));
}
/**
* 计算当前点与制定点之间的欧式距离
*
* @param p
* 待计算聚类的p点
* @return
*/
public double ouDistance(Point p) {
double distance = 0;
distance = (this.x - p.x) * (this.x - p.x) + (this.y - p.y)
* (this.y - p.y);
distance = Math.sqrt(distance);
return distance;
}
/**
* 判断2个坐标点是否为用个坐标点
*
* @param p
* 待比较坐标点
* @return
*/
public boolean isTheSame(Point p) {
boolean isSamed = false;
if (this.x == p.x && this.y == p.y) {
isSamed = true;
}
return isSamed;
}
}
package DataMining_KDTree;
/**
* 空间矢量,表示所代表的空间范围
*
* @author lyq
*
*/
public class Range {
// 边界左边界
double left;
// 边界右边界
double right;
// 边界上边界
double top;
// 边界下边界
double bottom;
public Range() {
this.left = -Integer.MAX_VALUE;
this.right = Integer.MAX_VALUE;
this.top = Integer.MAX_VALUE;
this.bottom = -Integer.MAX_VALUE;
}
public Range(int left, int right, int top, int bottom) {
this.left = left;
this.right = right;
this.top = top;
this.bottom = bottom;
}
/**
* 空间矢量进行并操作
*
* @param range
* @return
*/
public Range crossOperation(Range r) {
Range range = new Range();
// 取靠近右侧的左边界
if (r.left > this.left) {
range.left = r.left;
} else {
range.left = this.left;
}
// 取靠近左侧的右边界
if (r.right < this.right) {
range.right = r.right;
} else {
range.right = this.right;
}
// 取靠近下侧的上边界
if (r.top < this.top) {
range.top = r.top;
} else {
range.top = this.top;
}
// 取靠近上侧的下边界
if (r.bottom > this.bottom) {
range.bottom = r.bottom;
} else {
range.bottom = this.bottom;
}
return range;
}
/**
* 根据坐标点分割方向确定左侧空间矢量
*
* @param p
* 数据矢量
* @param dir
* 分割方向
* @return
*/
public static Range initLeftRange(Point p, int dir) {
Range range = new Range();
if (dir == KDTreeTool.DIRECTION_X) {
range.right = p.x;
} else {
range.bottom = p.y;
}
return range;
}
/**
* 根据坐标点分割方向确定右侧空间矢量
*
* @param p
* 数据矢量
* @param dir
* 分割方向
* @return
*/
public static Range initRightRange(Point p, int dir) {
Range range = new Range();
if (dir == KDTreeTool.DIRECTION_X) {
range.left = p.x;
} else {
range.top = p.y;
}
return range;
}
}
package DataMining_KDTree;
/**
* KD树节点
* @author lyq
*
*/
public class TreeNode {
//数据矢量
Point nodeData;
//分割平面的分割线
int spilt;
//空间矢量,该节点所表示的空间范围
Range range;
//父节点
TreeNode parentNode;
//位于分割超平面左侧的孩子节点
TreeNode leftNode;
//位于分割超平面右侧的孩子节点
TreeNode rightNode;
//节点是否被访问过,用于回溯时使用
boolean isVisited;
public TreeNode(){
this.isVisited = false;
}
}
package DataMining_KDTree;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.Stack;
/**
* KD树-k维空间关键数据检索算法工具类
*
* @author lyq
*
*/
public class KDTreeTool {
// 空间平面的方向
public static final int DIRECTION_X = 0;
public static final int DIRECTION_Y = 1;
// 输入的测试数据坐标点文件
private String filePath;
// 原始所有数据点数据
private ArrayList<Point> totalDatas;
// KD树根节点
private TreeNode rootNode;
public KDTreeTool(String filePath) {
this.filePath = filePath;
readDataFile();
}
/**
* 从文件中读取数据
*/
private void readDataFile() {
File file = new File(filePath);
ArrayList<String[]> dataArray = new ArrayList<String[]>();
try {
BufferedReader in = new BufferedReader(new FileReader(file));
String str;
String[] tempArray;
while ((str = in.readLine()) != null) {
tempArray = str.split(" ");
dataArray.add(tempArray);
}
in.close();
} catch (IOException e) {
e.getStackTrace();
}
Point p;
totalDatas = new ArrayList<>();
for (String[] array : dataArray) {
p = new Point(array[0], array[1]);
totalDatas.add(p);
}
}
/**
* 创建KD树
*
* @return
*/
public TreeNode createKDTree() {
ArrayList<Point> copyDatas;
rootNode = new TreeNode();
// 根据节点开始时所表示的空间时无限大的
rootNode.range = new Range();
copyDatas = (ArrayList<Point>) totalDatas.clone();
recusiveConstructNode(rootNode, copyDatas);
return rootNode;
}
/**
* 递归进行KD树的构造
*
* @param node
* 当前正在构造的节点
* @param datas
* 该节点对应的正在处理的数据
* @return
*/
private void recusiveConstructNode(TreeNode node, ArrayList<Point> datas) {
int direction = 0;
ArrayList<Point> leftSideDatas;
ArrayList<Point> rightSideDatas;
Point p;
TreeNode leftNode;
TreeNode rightNode;
Range range;
Range range2;
// 如果划分的数据点集合只有1个数据,则不再划分
if (datas.size() == 1) {
node.nodeData = datas.get(0);
return;
}
// 首先在当前的数据点集合中进行分割方向的选择
direction = selectSplitDrc(datas);
// 根据方向取出中位数点作为数据矢量
p = getMiddlePoint(datas, direction);
node.spilt = direction;
node.nodeData = p;
leftSideDatas = getLeftSideDatas(datas, p, direction);
datas.removeAll(leftSideDatas);
// 还要去掉自身
datas.remove(p);
rightSideDatas = datas;
if (leftSideDatas.size() > 0) {
leftNode = new TreeNode();
leftNode.parentNode = node;
range2 = Range.initLeftRange(p, direction);
// 获取父节点的空间矢量,进行交集运算做范围拆分
range = node.range.crossOperation(range2);
leftNode.range = range;
node.leftNode = leftNode;
recusiveConstructNode(leftNode, leftSideDatas);
}
if (rightSideDatas.size() > 0) {
rightNode = new TreeNode();
rightNode.parentNode = node;
range2 = Range.initRightRange(p, direction);
// 获取父节点的空间矢量,进行交集运算做范围拆分
range = node.range.crossOperation(range2);
rightNode.range = range;
node.rightNode = rightNode;
recusiveConstructNode(rightNode, rightSideDatas);
}
}
/**
* 搜索出给定数据点的最近点
*
* @param p
* 待比较坐标点
*/
public Point searchNearestData(Point p) {
// 节点距离给定数据点的距离
TreeNode nearestNode = null;
// 用栈记录遍历过的节点
Stack<TreeNode> stackNodes;
stackNodes = new Stack<>();
findedNearestLeafNode(p, rootNode, stackNodes);
// 取出叶子节点,作为当前找到的最近节点
nearestNode = stackNodes.pop();
nearestNode = dfsSearchNodes(stackNodes, p, nearestNode);
return nearestNode.nodeData;
}
/**
* 深度优先的方式进行最近点的查找
*
* @param stack
* KD树节点栈
* @param desPoint
* 给定的数据点
* @param nearestNode
* 当前找到的最近节点
* @return
*/
private TreeNode dfsSearchNodes(Stack<TreeNode> stack, Point desPoint,
TreeNode nearestNode) {
// 是否碰到父节点边界
boolean isCollision;
double minDis;
double dis;
TreeNode parentNode;
// 如果栈内节点已经全部弹出,则遍历结束
if (stack.isEmpty()) {
return nearestNode;
}
// 获取父节点
parentNode = stack.pop();
minDis = desPoint.ouDistance(nearestNode.nodeData);
dis = desPoint.ouDistance(parentNode.nodeData);
// 如果与当前回溯到的父节点距离更短,则搜索到的节点进行更新
if (dis < minDis) {
minDis = dis;
nearestNode = parentNode;
}
// 默认没有碰撞到
isCollision = false;
// 判断是否触碰到了父节点的空间分割线
if (parentNode.spilt == DIRECTION_X) {
if (parentNode.nodeData.x > desPoint.x - minDis
&& parentNode.nodeData.x < desPoint.x + minDis) {
isCollision = true;
}
} else {
if (parentNode.nodeData.y > desPoint.y - minDis
&& parentNode.nodeData.y < desPoint.y + minDis) {
isCollision = true;
}
}
// 如果触碰到父边界了,并且此节点的孩子节点还未完全遍历完,则可以继续遍历
if (isCollision
&& (!parentNode.leftNode.isVisited || !parentNode.rightNode.isVisited)) {
TreeNode newNode;
// 新建当前的小局部节点栈
Stack<TreeNode> otherStack = new Stack<>();
// 从parentNode的树以下继续寻找
findedNearestLeafNode(desPoint, parentNode, otherStack);
newNode = dfsSearchNodes(otherStack, desPoint, otherStack.pop());
dis = newNode.nodeData.ouDistance(desPoint);
if (dis < minDis) {
nearestNode = newNode;
}
}
// 继续往上回溯
nearestNode = dfsSearchNodes(stack, desPoint, nearestNode);
return nearestNode;
}
/**
* 找到与所给定节点的最近的叶子节点
*
* @param p
* 待比较节点
* @param node
* 当前搜索到的节点
* @param stack
* 遍历过的节点栈
*/
private void findedNearestLeafNode(Point p, TreeNode node,
Stack<TreeNode> stack) {
// 分割方向
int splitDic;
// 将遍历过的节点加入栈中
stack.push(node);
// 标记为访问过
node.isVisited = true;
// 如果此节点没有左右孩子节点说明已经是叶子节点了
if (node.leftNode == null && node.rightNode == null) {
return;
}
splitDic = node.spilt;
// 选择一个符合分割范围的节点继续递归搜寻
if ((splitDic == DIRECTION_X && p.x < node.nodeData.x)
|| (splitDic == DIRECTION_Y && p.y < node.nodeData.y)) {
if (!node.leftNode.isVisited) {
findedNearestLeafNode(p, node.leftNode, stack);
} else {
// 如果左孩子节点已经访问过,则访问另一边
findedNearestLeafNode(p, node.rightNode, stack);
}
} else if ((splitDic == DIRECTION_X && p.x > node.nodeData.x)
|| (splitDic == DIRECTION_Y && p.y > node.nodeData.y)) {
if (!node.rightNode.isVisited) {
findedNearestLeafNode(p, node.rightNode, stack);
} else {
// 如果右孩子节点已经访问过,则访问另一边
findedNearestLeafNode(p, node.leftNode, stack);
}
}
}
/**
* 根据给定的数据点通过计算反差选择的分割点
*
* @param datas
* 部分的集合点集合
* @return
*/
private int selectSplitDrc(ArrayList<Point> datas) {
int direction = 0;
double avgX = 0;
double avgY = 0;
double varianceX = 0;
double varianceY = 0;
for (Point p : datas) {
avgX += p.x;
avgY += p.y;
}
avgX /= datas.size();
avgY /= datas.size();
for (Point p : datas) {
varianceX += (p.x - avgX) * (p.x - avgX);
varianceY += (p.y - avgY) * (p.y - avgY);
}
// 求最后的方差
varianceX /= datas.size();
varianceY /= datas.size();
// 通过比较方差的大小决定分割方向,选择波动较大的进行划分
direction = varianceX > varianceY ? DIRECTION_X : DIRECTION_Y;
return direction;
}
/**
* 根据坐标点方位进行排序,选出中间点的坐标数据
*
* @param datas
* 数据点集合
* @param dir
* 排序的坐标方向
*/
private Point getMiddlePoint(ArrayList<Point> datas, int dir) {
int index = 0;
Point middlePoint;
index = datas.size() / 2;
if (dir == DIRECTION_X) {
Collections.sort(datas, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
// TODO Auto-generated method stub
return o1.x.compareTo(o2.x);
}
});
} else {
Collections.sort(datas, new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
// TODO Auto-generated method stub
return o1.y.compareTo(o2.y);
}
});
}
// 取出中位数
middlePoint = datas.get(index);
return middlePoint;
}
/**
* 根据方向得到原部分节点集合左侧的数据点
*
* @param datas
* 原始数据点集合
* @param nodeData
* 数据矢量
* @param dir
* 分割方向
* @return
*/
private ArrayList<Point> getLeftSideDatas(ArrayList<Point> datas,
Point nodeData, int dir) {
ArrayList<Point> leftSideDatas = new ArrayList<>();
for (Point p : datas) {
if (dir == DIRECTION_X && p.x < nodeData.x) {
leftSideDatas.add(p);
} else if (dir == DIRECTION_Y && p.y < nodeData.y) {
leftSideDatas.add(p);
}
}
return leftSideDatas;
}
}
package DataMining_KDTree;
import java.text.MessageFormat;
/**
* KD树算法测试类
*
* @author lyq
*
*/
public class Client {
public static void main(String[] args) {
String filePath = "C:\Users\lyq\Desktop\icon\input.txt";
Point queryNode;
Point searchedNode;
KDTreeTool tool = new KDTreeTool(filePath);
// 进行KD树的构建
tool.createKDTree();
// 通过KD树进行数据点的最近点查询
queryNode = new Point(2.1, 3.1);
searchedNode = tool.searchNearestData(queryNode);
System.out.println(MessageFormat.format(
"距离查询点({0}, {1})最近的坐标点为({2}, {3})", queryNode.x, queryNode.y,
searchedNode.x, searchedNode.y));
//重新构造KD树,去除之前的访问记录
tool.createKDTree();
queryNode = new Point(2, 4.5);
searchedNode = tool.searchNearestData(queryNode);
System.out.println(MessageFormat.format(
"距离查询点({0}, {1})最近的坐标点为({2}, {3})", queryNode.x, queryNode.y,
searchedNode.x, searchedNode.y));
}
}
距离查询点(2.1, 3.1)最近的坐标点为(2, 3)
距离查询点(2, 4.5)最近的坐标点为(2, 3)算法的输出结果与期望值还是一致的。
目前KD-Tree的使用场景是SIFT算法做特征点匹配的时候使用到了,特征点匹配指的是通过距离函数在高维矢量空间进行相似性检索。
参考文献:百度百科 http://baike.baidu.com