最短路径问题----Dijkstra算法的解释

先上图：

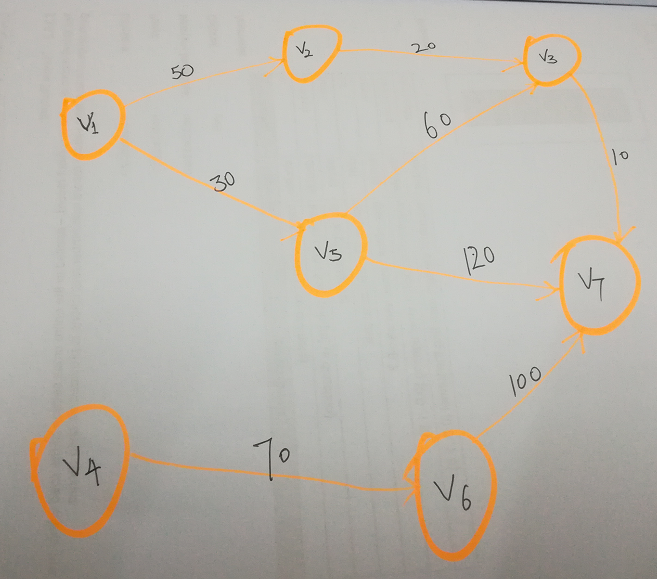
现在要找到地点V1到其余各个地点的最短路径（图中数字的单位默认为km.）。有一个原则是：永远找最小，确保无更小。

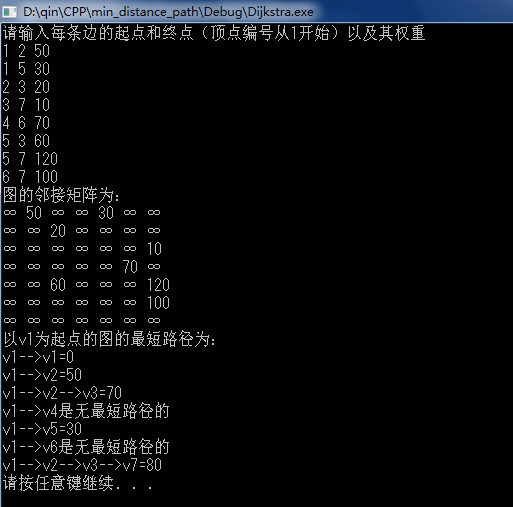
第一步：v1->v1,v1->v2,...v1->v7的距离用一维数组dis[0],dis[1],dis[2],...dis[6]表示。初始化数组：dis=[0 50 inf inf 30 inf inf];

第二步：找到dis数组中的最小值(注意不算v1->v1=0)，它是dis[4]=30;这个距离就是v1->v5的最小距离了，因为所有的距离都是正数，如果你从v1出发，通过其他顶点绕路绕到v5,那总距离肯定大于30，因为30+（一个大于0的数）肯定大于30.此时，找到了v1->v5的最短路径；

第三步：把顶点v5置为true,代表顶点v5已被访问；

第四步：看v5通往里，从图上可以看到v5通往v3和v7,v5->v3的距离是60，v5->v7的距离是120，所以通过v5中转到v3和v7后，v1->v3的距离变成30+60=90，v1->v7的距离变成30+120=150；这对dis数组中保存的v1到其它各个顶点的距离产生了影响， 此时就用更小的值去更新dis数组中的值。更新后的dis数组是：dis=[0 50 90 inf 30 inf 150].(注：inf代表无穷大)

第五步：找dis数组中除去v1->v5=30这个值之后的最小值，它是v1->v2=50，找到后把顶点v2置为ture.

第六步：从v1出发，通过v2中转，看v2会到达哪里。可以看到，v2->v3=20,这时更新dis数组中v1->v3值，把90更新成70.此时数组dis=[0 50 70 inf 30 inf 150].

第七步：重复第5步，找排除掉顶点是ture的值后，剩余的数的最小值，它是v1->v3=70，把顶点v3置为true.

第八步：从v1出发，通过v3中转，看v3会到达哪里。可以看到，v3->v7=10,这时更新dis数组中v1->v7值，把150更新成80.此时数组dis=[0 50 70 inf 30 inf 80].

第九步：结束！

最终结果：

以下C++代码来源于：https://blog.csdn.net/qq_35644234/article/details/60870719

 Dijkstra.h文件的代码：

/************************************************************/
/*                程序作者：Willam                          */
/*                程序完成时间：2017/3/8                    */
/*                有任何问题请联系：2930526477@qq.com       */
/************************************************************/
//@尽量写出完美的程序

#pragma once
//#pragma once是一个比较常用的C/C++杂注，
//只要在头文件的最开始加入这条杂注，
//就能够保证头文件只被编译一次。

#include<iostream>
#include<string>
using namespace std;

/*
本程序是使用Dijkstra算法实现求解最短路径的问题
采用的邻接矩阵来存储图
*/
//记录起点到每个顶点的最短路径的信息
struct Dis {
    string path;
    int value;
    bool visit;
    Dis() {
        visit = false;
        value = 0;
        path = "";
    }
};

class Graph_DG {
private:
    int vexnum;   //图的顶点个数
    int edge;     //图的边数
    int **arc;   //邻接矩阵
    Dis * dis;   //记录各个顶点最短路径的信息
public:
    //构造函数
    Graph_DG(int vexnum, int edge);
    //析构函数
    ~Graph_DG();
    // 判断我们每次输入的的边的信息是否合法
    //顶点从1开始编号
    bool check_edge_value(int start, int end, int weight);
    //创建图
    void createGraph();
    //打印邻接矩阵
    void print();
    //求最短路径
    void Dijkstra(int begin);
    //打印最短路径
    void print_path(int);
};

Dijkstra.cpp文件的代码：

#include"Dijkstra.h"

//构造函数
Graph_DG::Graph_DG(int vexnum, int edge) {
    //初始化顶点数和边数
    this->vexnum = vexnum;//this 代表调用构造函数的那一个一个对象的地址
    this->edge = edge;
    //为邻接矩阵开辟空间和赋初值
    arc = new int*[this->vexnum];//arc 是二级指针
    dis = new Dis[this->vexnum];
    for (int i = 0; i < this->vexnum; i++) {
        arc[i] = new int[this->vexnum];
        for (int k = 0; k < this->vexnum; k++) {
            //邻接矩阵初始化为无穷大
            arc[i][k] = INT_MAX;
        }
    }
}
//析构函数
Graph_DG::~Graph_DG() {
    delete[] dis;
    for (int i = 0; i < this->vexnum; i++) {
        delete this->arc[i];
    }
    delete arc;
}

// 判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool Graph_DG::check_edge_value(int start, int end, int weight) {
    if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {
        return false;
    }
    return true;
}

void Graph_DG::createGraph() {
    cout << "请输入每条边的起点和终点（顶点编号从1开始）以及其权重" << endl;
    int start;
    int end;
    int weight;
    int count = 0;
    while (count != this->edge) {
        cin >> start >> end >> weight;
        //首先判断边的信息是否合法
        while (!this->check_edge_value(start, end, weight)) {
            cout << "输入的边的信息不合法，请重新输入" << endl;
            cin >> start >> end >> weight;
        }
        //对邻接矩阵对应上的点赋值
        arc[start - 1][end - 1] = weight;
        //无向图添加上这行代码
        //arc[end - 1][start - 1] = weight;
        ++count;
    }
}

void Graph_DG::print() {
    cout << "图的邻接矩阵为：" << endl;
    int count_row = 0; //打印行的标签
    int count_col = 0; //打印列的标签
    //开始打印
    while (count_row != this->vexnum) {
        count_col = 0;
        while (count_col != this->vexnum) {
            if (arc[count_row][count_col] == INT_MAX)
                cout << "∞" << " ";
            else
                cout << arc[count_row][count_col] << " ";
            ++count_col;
        }
        cout << endl;
        ++count_row;
    }
}
void Graph_DG::Dijkstra(int begin){
    //首先初始化我们的dis数组
    int i;
    for (i = 0; i < this->vexnum; i++) {
        //设置当前的路径
        dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + 1);
        dis[i].value = arc[begin - 1][i];
    }
    //设置起点的到起点的路径为0
    dis[begin - 1].value = 0;
    dis[begin - 1].visit = true;

    int count = 1;
    //计算剩余的顶点的最短路径（剩余this->vexnum-1个顶点）
    while (count != this->vexnum) {
        //temp用于保存当前dis数组中最小的那个下标
        //min记录的当前的最小值
        int temp = 0;
        int min = INT_MAX;
        for (i = 0; i < this->vexnum; i++) {
            if (!dis[i].visit && dis[i].value<min) {
                min = dis[i].value;
                temp = i;
            }
        }
        //cout << temp + 1 << "  "<<min << endl;
        //把temp对应的顶点加入到已经找到的最短路径的集合中
        dis[temp].visit = true;
        ++count;
        for (i = 0; i < this->vexnum; i++) {
            //注意这里的条件arc[temp][i]!=INT_MAX必须加，不然会出现溢出，从而造成程序异常
            if (!dis[i].visit && arc[temp][i] != INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
                //如果新得到的边可以影响其他为访问的顶点，那就更新它的最短路径和长度
                dis[i].value = dis[temp].value + arc[temp][i];
                dis[i].path = dis[temp].path + "-->v" + to_string(i + 1);
            }
        }
    }

}
void Graph_DG::print_path(int begin) {
    string str;
    str = "v" + to_string(begin);
    cout << "以" << str << "为起点的图的最短路径为：" << endl;
    for (int i = 0; i != this->vexnum; i++) {
        if (dis[i].value != INT_MAX)
            cout << dis[i].path << "=" << dis[i].value << endl;
        else {
            cout << dis[i].path << "是无最短路径的" << endl;
        }
    }
}

main.cpp文件的代码：

#include"Dijkstra.h"


//检验输入边数和顶点数的值是否有效，可以自己推算为啥：
//顶点数和边数的关系是：((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
    if (Vexnum <= 0 || edge <= 0 || ((Vexnum*(Vexnum - 1)) / 2) < edge)
        return false;
    return true;
}
int main() {
    int vexnum; int edge;

    cout << "输入图的顶点个数和边的条数：" << endl;
    cin >> vexnum >> edge;
    while (!check(vexnum, edge)) {
        cout << "输入的数值不合法，请重新输入" << endl;
        cin >> vexnum >> edge;
    }
    Graph_DG graph(vexnum, edge);
    graph.createGraph();
    graph.print();
    graph.Dijkstra(1);
    graph.print_path(1);
    system("pause");
    return 0;
}

运行结果：

---