目录
- 最小二乘法的原理与要解决的问题
- 最小二乘法的代数法解法
- 最小二乘法的矩阵法解法
- 最小二乘法的局限性和适用场景
- 常见问题
最小二乘法是用来做函数拟合或者求函数极值的方法。在机器学习,尤其是回归模型中,经常可以看到最小二乘法的身影,这里就对我对最小二乘法的认知做一个小结。
一、最小二乘法的原理与要解决的问题
最小二乘法是由勒让德在19世纪发现的(也有争议为高斯发明),形式如下式:

观测值就是我们的多组样本,理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数,我们的目标是得到使目标函数最小化时候的拟合函数的模型。举一个最简单的线性回归的简单例子,比如我们有m个只有一个特征的样本:

二、最小二乘法的代数法解法
上面提到要使J(θ0,θ1)最小,方法就是对θ0和θ1分别来求偏导数,令偏导数为0,得到一个关于θ0和θ1的二元方程组。求解这个二元方程组即可。

这个方法很容易推广到多个样本特征的线性拟合。

这样我们得到一个N+1元一次方程组,这个方程组有N+1个方程,求解这个方程,就可以得到所有的N+1个未知的θ。
这个方法很容易推广到多个样本特征的非线性拟合。原理和上面的一样,都是用损失函数对各个参数求导取0,然后求解方程组得到参数值。这里就不累述了。
三、最小二乘法的矩阵法解法
矩阵法比代数法要简洁,且矩阵运算可以取代循环,所以现在很多书和机器学习库都是用的矩阵法来做最小二乘法。这里用上面的多元线性回归例子来描述矩阵法解法。在我的博客【1】中已经使用到:
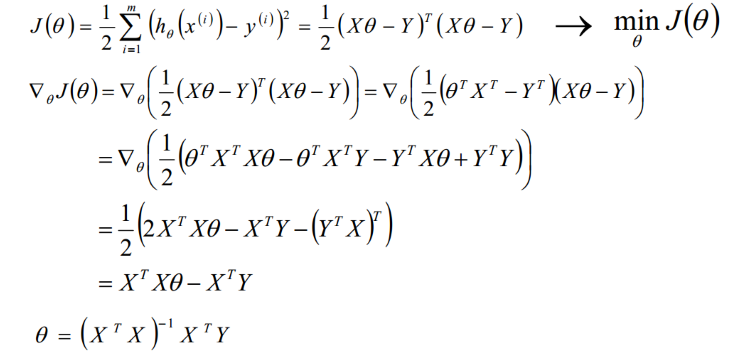
四、最小二乘法的局限性和适用场景
从上面可以看出,最小二乘法适用简洁高效,比梯度下降这样的迭代法似乎方便很多。但是这里我们就聊聊最小二乘法的局限性。


- 如果拟合函数不是线性的,这时无法使用最小二乘法,需要通过一些技巧转化为线性才能使用,此时梯度下降仍然可以用。
- 当样本量m很少,小于特征数n的时候,这时拟合方程是欠定的,常用的优化方法都无法去拟合数据。当样本量m等于特征数n的时候,用方程组求解就可以了。当m大于n时,拟合方程是超定的,也就是我们常用与最小二乘法的场景了。
五、常见问题
1) 对于多元函数求其极值,即使求偏导并令偏导数为0,也不能代表所求的值为极值点,也可能是拐点吧?
回答: 是的,不一定是全局极值点。只有数据集是凸的情况下,是全局的极值点。
2)假设函数非凸,求偏导之后,应该会求出多个值。此时这些值,应该是局部最优、或者拐点及全局最优解。如何判定这些值属于什么情况? 需要代入计算么?
回答:一般不用,这是理论上的情况,实际应用中局部最优也可以满足要求。
3)对于一元函数,可导必连续,连续未必可导。而对于多元函数而言,两者没有必然联系。如果存在不可导的情况,又该如何解决呢? 比如用梯度下降法求极值时,如何确保函数是连续的?如何确保函数在某点可导?
回答:对于无法连续可导的情况,比如L1正则化,一般可以用坐标轴下降法和最小角回归法来迭代求解极值。
4)是否可能存在损失函数为单调函数,那这样的话,不是没有极值了?
回答:这也有可能,但是我们总可以迭代找到局部最优的极小值。
5)如果存在调参时,正好选择的区间处于拐点区间。梯度下降法又是以梯度值接近0为判定条件,这样的话,应该会造成错误的参数选择吧。这个感觉还和局部最优解不一样。
回答:是的,所以一般需要多选择几个初始值分别梯度下降,找里面最优的局部最优解。
6)对于单调函数而言,其梯度是很难找到接近0的情况(除非是拐点)。。如何能通过迭代找到局部最优解呢?--比如X^3这样的函数,是单调递增的,X=0时是拐点,那是将X=0作为最优解了?
回答: 一般机器学习都是定义损失函数,损失最小为0,所以肯定会有拐点。拐点附近的局部最优解容易被找到。
附件一:手写推导过程练习
