目录
- 为什么要初始化
- 公式推导
- 初始化方法
- 引入激活函数
-
初始化方法分类
一、为什么要初始化
在深度学习中,神经网络的权重初始化方法(weight initialization)对模型的收敛速度和性能有着至关重要的影响。简单而言:神经网络其实就是对权重参数w的不停迭代更新,以期达到较好的性能。但随着层数的增多,极易出现梯度消失或者梯度爆炸。因此,对权重w的初始化则显得至关重要,一个好的权重初始化虽然不能完全解决梯度消失和梯度爆炸的问题,但是对于处理这两个问题是有很大的帮助的,并且十分有利于模型性能和收敛速度。
一般地,假定输入的每个特征是服从均值为0,方差为1的分布(一般输入到神经网络的数据都是要做归一化的,就是为了达到这个条件)。为了使网络中的信息更好的传递,每一层的特征的方差应该尽可能相等,如果保证这个特征的方差是相等的呢。我们可以从初始化的权重值入手。
二、公式推导
为了使网络中的信息更好的传递,每一层的特征的方差应该尽可能相等,基于此,可以分析每一层的网络初始化的权重应该满足哪些条件。首先来做一个公式推导:

在这里假定了x的均值为0,对于初始化的权重通常均值也是选择0,因此上面的式子可以转换成
![]()
又因为x中每个特征我们都假定方差为1,因此上面的式子可以改写成
![]()
现在要使得var(s)=1,则有
![]()

为了确保量纲和期望一致,我们将方差转换成标准差,因此要确保标准差为1/√n
三、初始化方法
现在我们来看看每种方法初始化时我们该如何设置方差能保证输入的分布状态不变。
3.1 均匀分布
对于均匀分布U(a,b),其期望和方差分别为
![]()
假定均匀分布为
![]()
在这里d为神经元的个数,则有期望和方差为
![]()
根据代入到下面表达式中,
![]()
可以得到:
![]()
因此为了保证最终的方差为1,因此方差需要乘以3,标准差则需要乘以√3。因此一般均匀分布的初始化值可以选择
![]()
在在xavier uniform init(也称glorot uniform,是2010年Xavier glorot发明的),在tensorflow中有对饮的API: tf.glorot_uniform_initializer()方法中初始化值为如下,在一个二维矩阵中din,dout分别表示矩阵的第一个维度和第二个维度。
![]()
1)举例说明——tf.random_uniform_initializer()
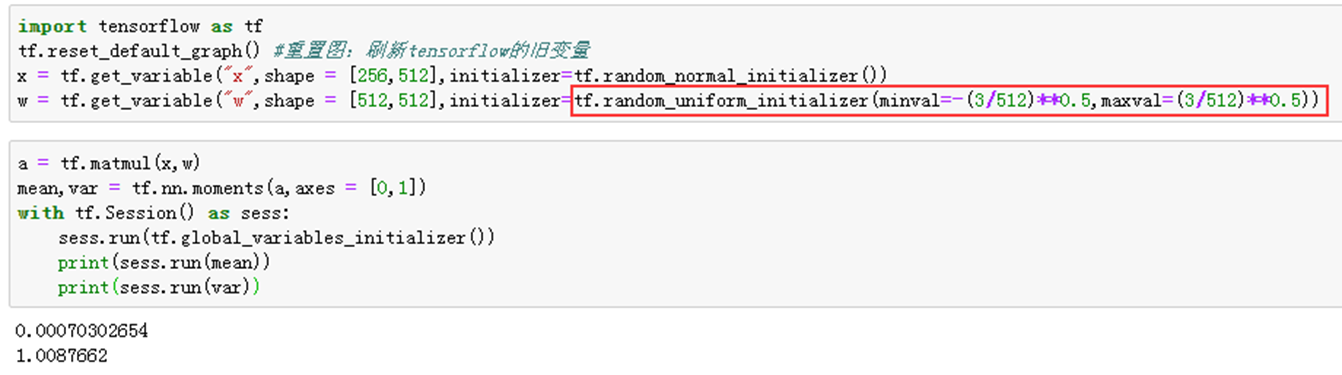
2)举例说明——tf.glorot_uniform_initializer()

3.2 正态分布
正态分布会直接给出期望和标准差,所以这个不用多说。为了保证var(s)=1,我们需要让var(w)=1/d,则标准差为1/√d。
同样还是从两个方面来展示,第一个随机取值,设置方差为:1/√d,xavier uniform init内部有定义,其标准差为:

1)举例说明——tf.random_normal_initializer()

2)举例说明——tf.glorot_normal_initializer()

3.3 常数初始化
常数初始化时期望为常数值n,方差为0。
1)举例说明——tf.zeros_initializer()

2)举例说明——tf.ones_initializer()
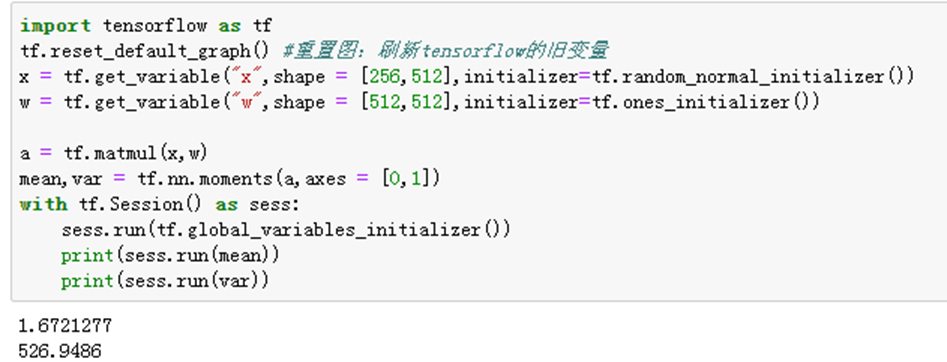
3)举例说明——tf.constant_initializer()

从上面实验可以看出,初始权重为0时,mean和VAR为0,无法有效计算;当取1或者常数时候,会较大变化。
四、引入激活函数
上面都是在线性运算的情况下的结果,但实际应用中都是要引入激活函数的,这样神经网络才具有更强的表达能力。如果引入激活函数会怎么样?为了观看效果,我们将网络层数设置为100层,分别采用tf.random_normal_initializer()和tf.glorot_normal_initializer()。
1-1)举例说明——tf.random_normal_initializer(),不加激活函数

1-2)举例说明——tf.random_normal_initializer(),加tanh函数
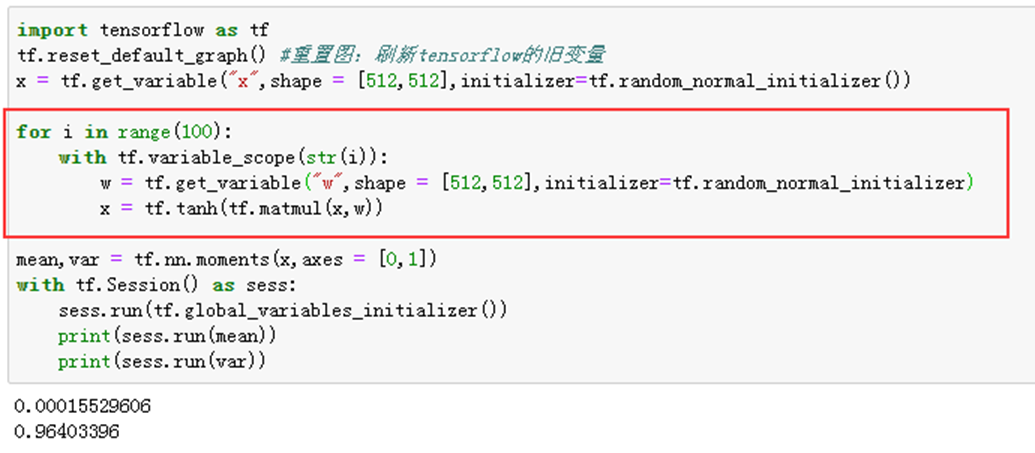
1-3)举例说明——tf.random_normal_initializer(),加relu函数

2-1)举例说明——tf.glorot_normal_initializer(),不加激活函数

2-2)举例说明——tf.glorot_normal_initializer(),加tanh函数

2-3)举例说明——tf.glorot_normal_initializer(),加relu函数

3)举例说明——tf.random_normal_initializer(stddev = (2/512)**0.5),加relu函数
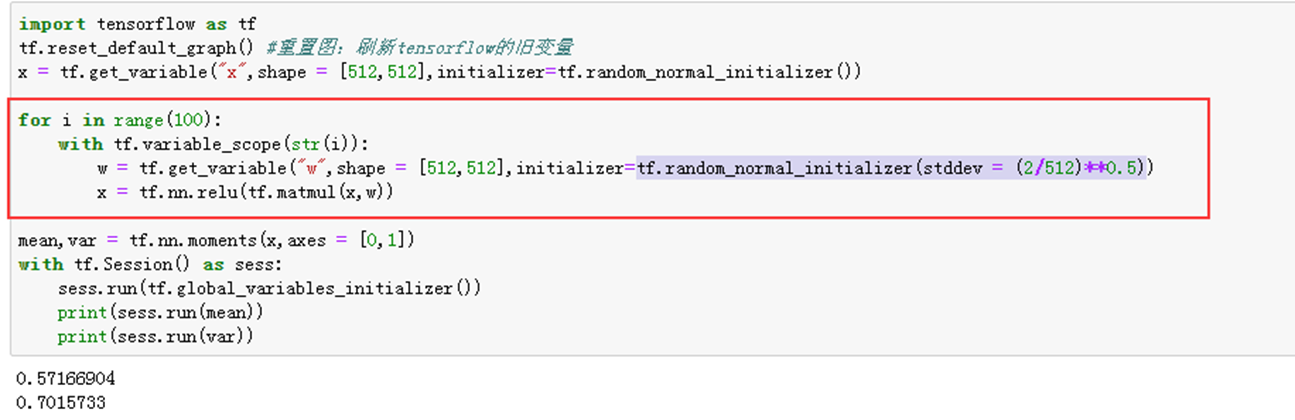
实验说明:
1、2-3实验说明relu函数并不适用tf.glorot_normal_initializer(),1-3实验说明初始化的tf.random_normal_initializer(mean=0.0, stddev=1.0, seed=None, dtype=tf.float32)原型结合也不好,3实验说明调整后的tf.random_normal_initializer有较好的效果。对于relu激活函数时,正态分布的标准差通常为
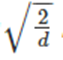
2、实验出现NAN,表明有指数爆炸发生。
五、初始化方法分类
- 随机初始化
- Xavier初始化:tf.glorot_normal_initializer()
- Kaiming初始化(he初始化):其实就是上一节中实验3的部分:tf.random_normal_initializer(stddev = (2/512)**0.5)。
附件一:第三节实验
import tensorflow as tf tf.reset_default_graph() #重置图:刷新tensorflow的旧变量 x = tf.get_variable("x",shape = [256,512],initializer=tf.random_normal_initializer()) w = tf.get_variable("w",shape = [512,512],initializer=tf.glorot_normal_initializer) a = tf.matmul(x,w) mean,var = tf.nn.moments(a,axes = [0,1]) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) print(sess.run(mean)) print(sess.run(var))
附件二:第四章实验3
import tensorflow as tf tf.reset_default_graph() #重置图:刷新tensorflow的旧变量 x = tf.get_variable("x",shape = [512,512],initializer=tf.random_normal_initializer()) for i in range(100): with tf.variable_scope(str(i)): w = tf.get_variable("w",shape = [512,512],initializer=tf.random_normal_initializer(stddev = (2/512)**0.5)) x = tf.nn.relu(tf.matmul(x,w)) mean,var = tf.nn.moments(x,axes = [0,1]) with tf.Session() as sess: sess.run(tf.global_variables_initializer()) print(sess.run(mean)) print(sess.run(var))
参考:
【1】初始化方法:https://www.cnblogs.com/jiangxinyang/p/11574049.html
【2】从最基本的方法到xavier、he初始化方法一路走来的历程:https://zhuanlan.zhihu.com/p/86602524