实现一个简单的线性回归(mxnet)
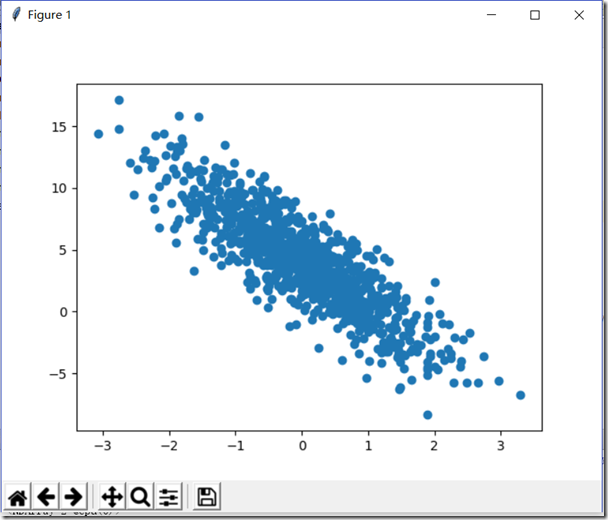
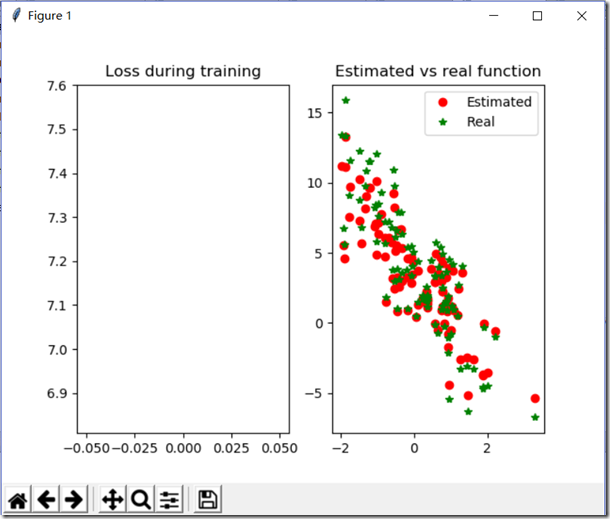
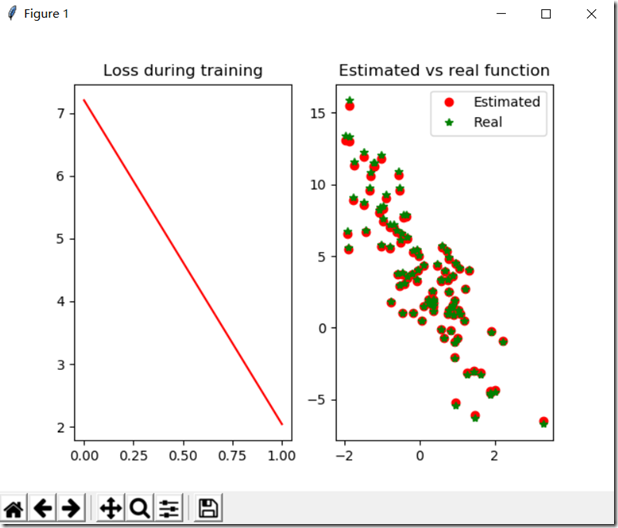
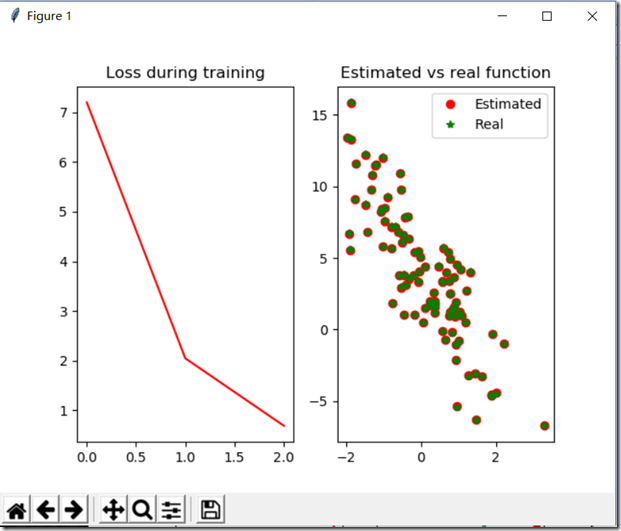
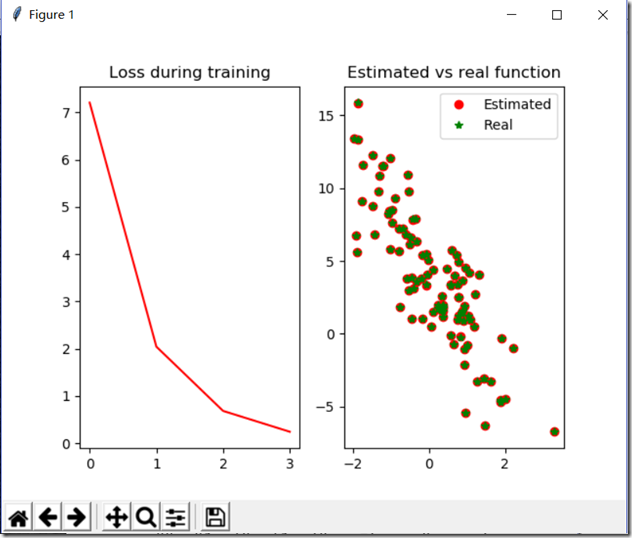
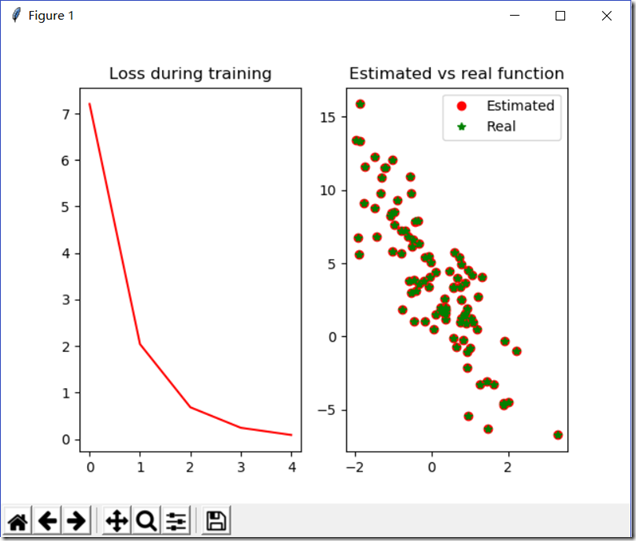
from mxnet import ndarray as nd from mxnet import autograd import matplotlib.pyplot as plt import random num_input=2#变量数 num_examples=1000#1000个样例 true_w=[2,-3.4]#真实的系数W true_b=4.2#真实的偏倚b X=nd.random_normal(shape=(num_examples,num_input))#随机产生数据 y=true_w[0]*X[:,0]+true_w[1]*X[:,1]+true_b#得到y值 y+=0.01*nd.random_normal(shape=y.shape)#加噪声 print(X[0],y[0]) plt.scatter(X[:,1].asnumpy(),y.asnumpy())#必须转换为numpy才能绘图 plt.show() batch_size=10#batch大小 def data_iter(): idx=list(range(num_examples)) random.shuffle(idx)#打乱数组 for i in range(0,num_examples,batch_size):#步长为10 j=nd.array(idx[i:min(i+batch_size,num_examples)]) yield nd.take(X,j),nd.take(y,j) for data,label in data_iter():#从data_liter()中提取 print(data,label) break w=nd.random_normal(shape=(num_input,1))#初始化 b=nd.zeros((1,))#初始化 params=[w,b]#参数合一 for param in params: param.attach_grad()#给参数的梯度赋予空间 def net(X):#设置网络 return nd.dot(X,w)+b def square_loss(yhat,y):#设置损失函数 return (yhat-y.reshape(yhat.shape))**2 def SGD(params,lr):#随机梯度下降函数 for param in params:#对每个参数使用随机梯度下降 param[:]=param-lr*param.grad#param.grad是自动求导的值 def real_fn(X):#真实的函数 return 2*X[:,0]-3.4*X[:,1]+4.2 def plot(losses,X,sample_size=100):#绘图 xs=list(range(len(losses))) f=plt.figure() fg1=f.add_subplot(121) fg2=f.add_subplot(122) fg1.set_title('Loss during training') fg1.plot(xs,losses,'r') fg2.set_title('Estimated vs real function') fg2.plot(X[:sample_size,1].asnumpy(),net(X[:sample_size,:]).asnumpy(),'or',label='Estimated') fg2.plot(X[:sample_size,1].asnumpy(),real_fn(X[:sample_size,:]).asnumpy(),'*g',label='Real') fg2.legend() plt.show() epochs = 5 learning_rate = .001 niter = 0 losses = [] moving_loss = 0 smoothing_constant = .01 # 训练 for e in range(epochs):#五次更新权重 total_loss = 0 for data, label in data_iter(): with autograd.record(): output = net(data)#预测值 loss = square_loss(output, label) loss.backward() SGD(params, learning_rate) total_loss += nd.sum(loss).asscalar()#转换为标量求和 # 记录每读取一个数据点后,损失的移动平均值的变化; niter +=1 curr_loss = nd.mean(loss).asscalar() moving_loss = (1 - smoothing_constant) * moving_loss + (smoothing_constant) * curr_loss # correct the bias from the moving averages est_loss = moving_loss/(1-(1-smoothing_constant)**niter)
结果:
线性回归 — 使用Gluon
from mxnet import ndarray as nd from mxnet import autograd from mxnet import gluon num_inputs=2 num_examples=1000 true_w=[2,-3.4] true_b=4.2 X=nd.random_normal(shape=(num_examples,num_inputs)) y=true_w[0]*X[:,0]+true_w[1]*X[:,1]+true_b y+=0.01*nd.random_normal(shape=y.shape) #数据读取 batch_size=10 dataset=gluon.data.ArrayDataset(X,y) data_iter=gluon.data.DataLoader(dataset,batch_size,shuffle=True) for data,label in data_iter: print(data,label) break net=gluon.nn.Sequential() net.add(gluon.nn.Dense(1)) net.initialize() square_loss=gluon.loss.L2Loss() trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.1}) epoch=5 batch_size=10 for e in range(epoch): total_loss=0 for data,label in data_iter: with autograd.record(): output=net(data) loss=square_loss(output,label) loss.backward() trainer.step(batch_size) total_loss+=nd.sum(loss).asscalar() print("Epoch %d average loss:%f"%(e,total_loss/num_examples))