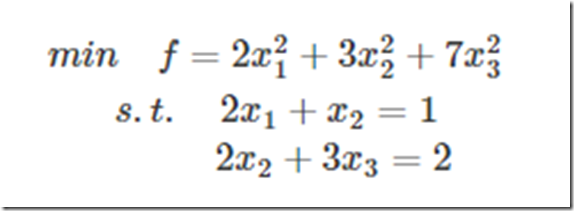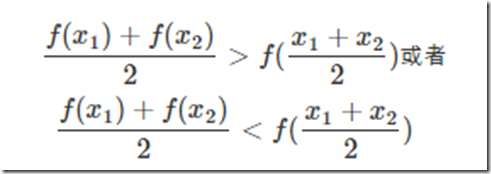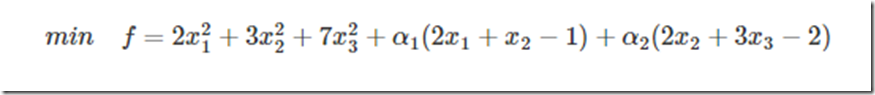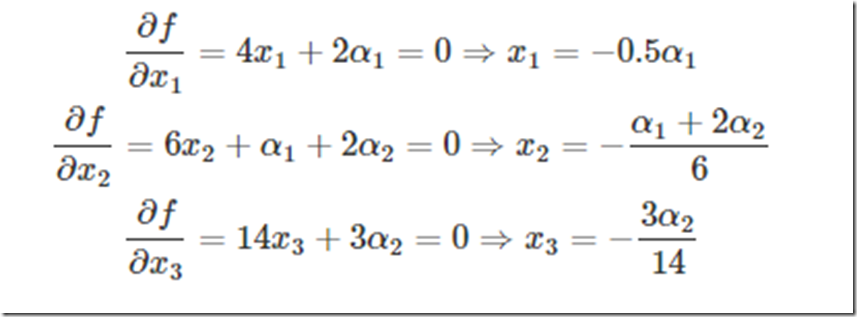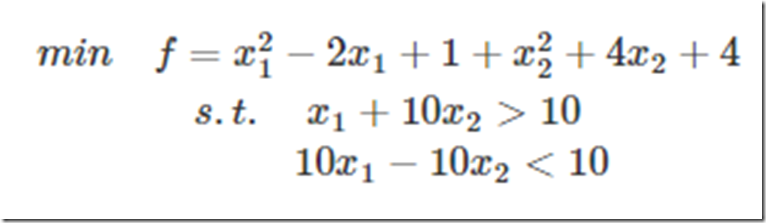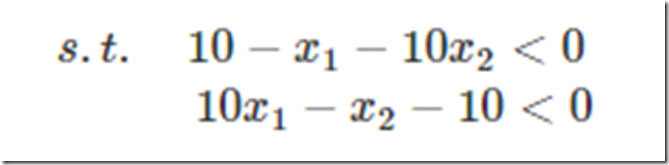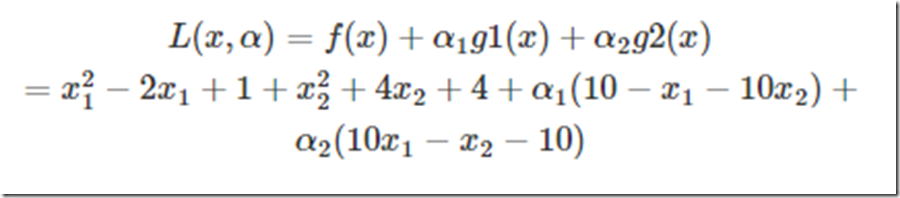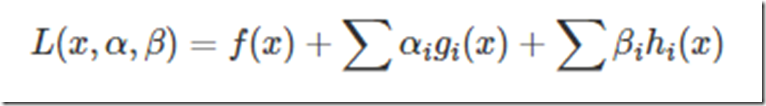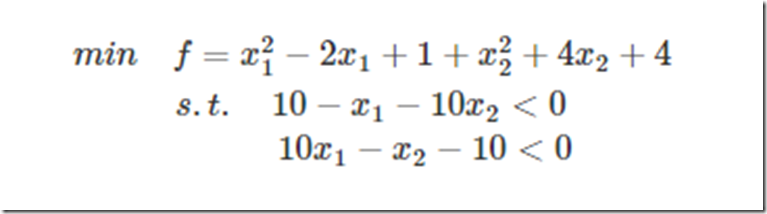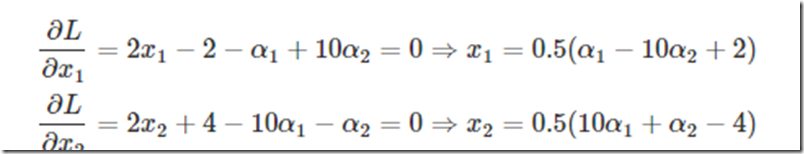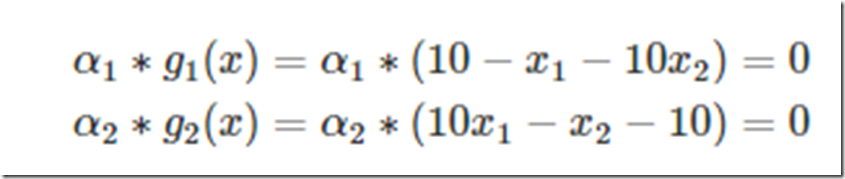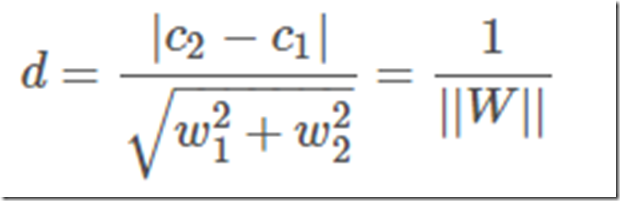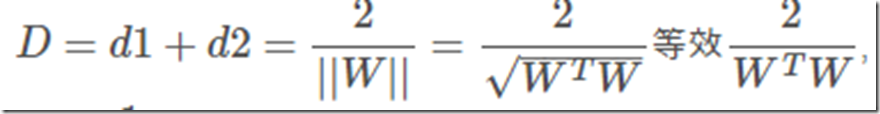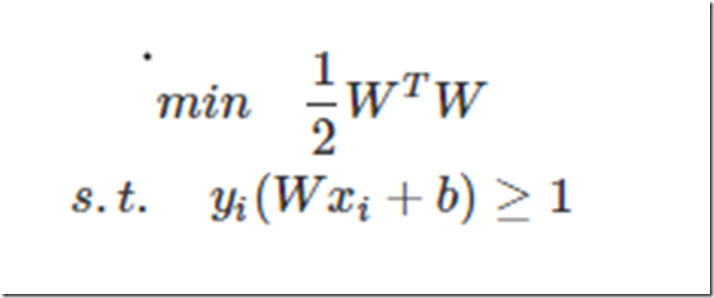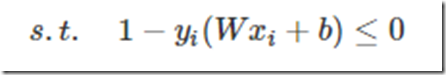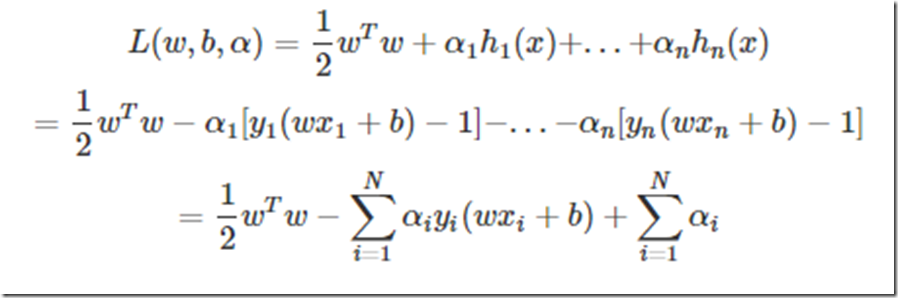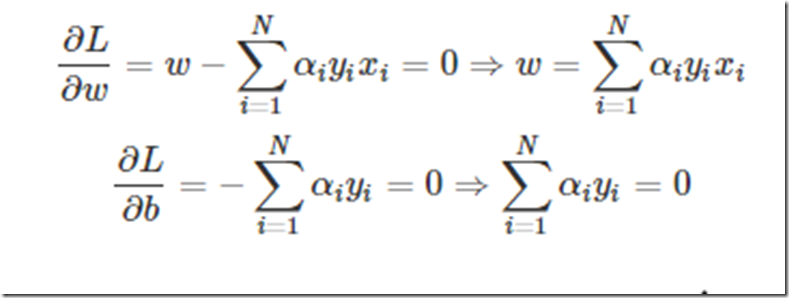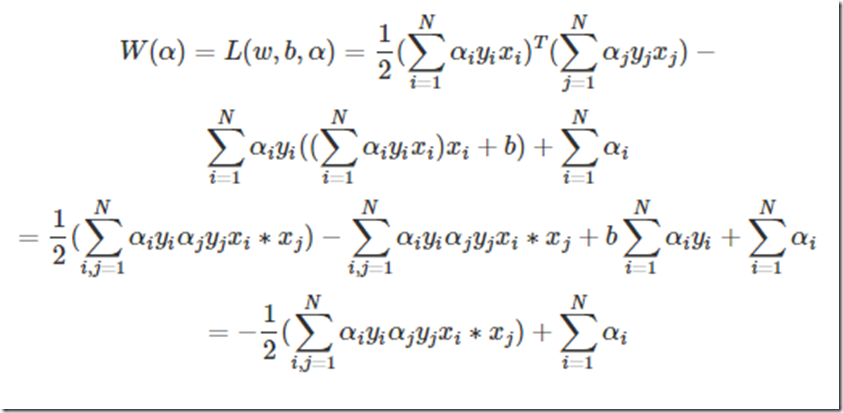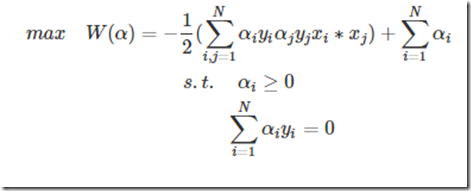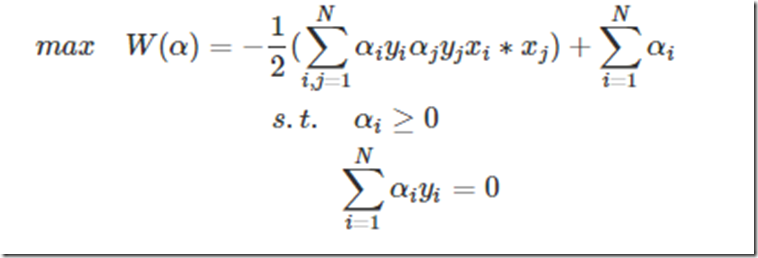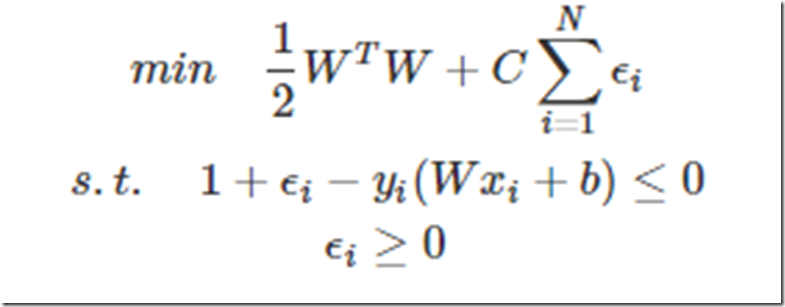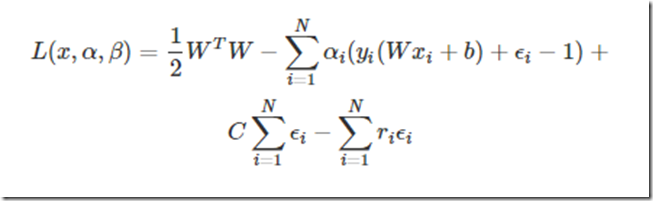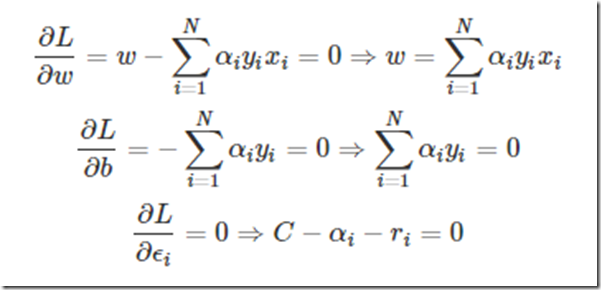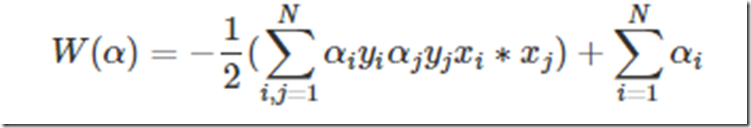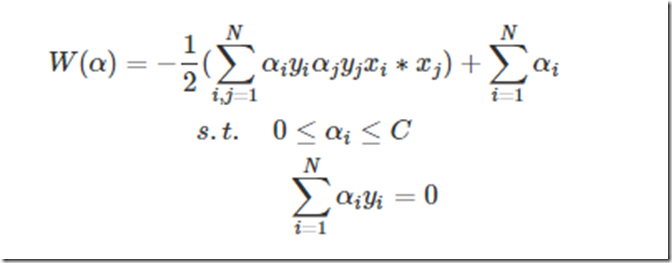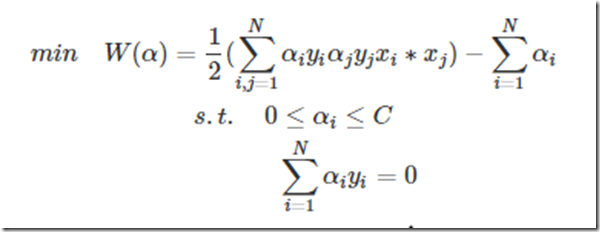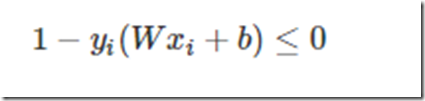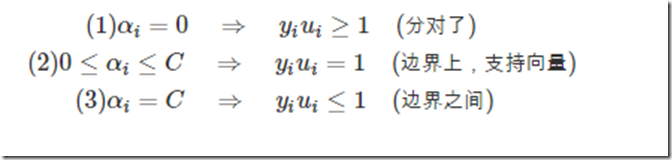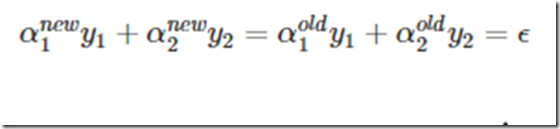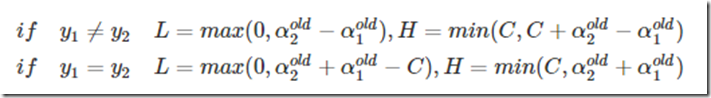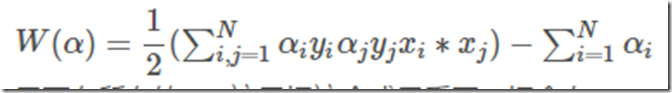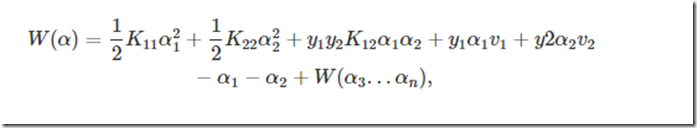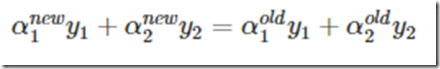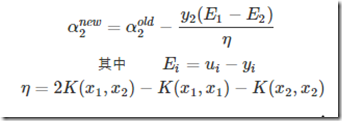一、拉格朗日乘子法
一般,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。这里我们先介绍拉格朗日乘子法,后面再介绍KKT条件。
比如考虑下面的组合优化的问题,
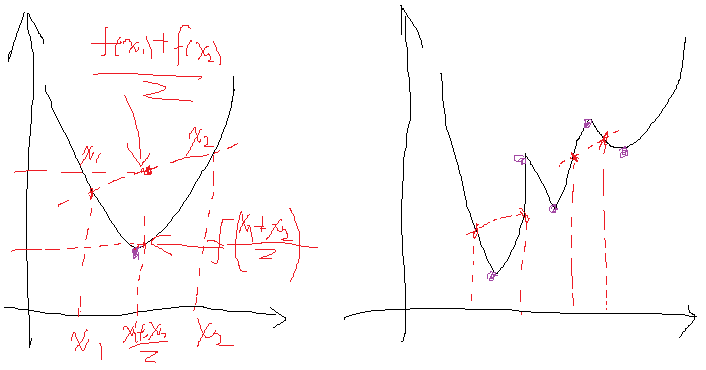
这是一个带等式约束的优化问题,有目标值,有约束条件。那么想想假设没有约束条件这个问题是怎么求解的呢?是不是直接f对各个x求导等于0,,解x就可以了,可以看到没有约束的话,求导为0,那么各个x均为0吧,这样f=0了,最小。但是x都为0不满足约束条件呀,那么问题就来了。这里在说一点的是,为什么上面说求导为0就可以呢?理论上多数问题是可以的,但是有的问题不可以。如果求导为0一定可以的话,那么f一定是个凸优化问题,什么是凸的呢?像下面这个左图:
凸的就是开口朝一个方向(向上或向下)。更准确的数学关系就是:
再来看看有约束的问题,既然有了约束不能直接求导,那么如果把约束去掉不就可以了吗?怎么去掉呢?这才需要拉格朗日方法。既然是等式约束,那么我们把这个约束乘一个系数加到目标函数中去,这样就相当于既考虑了原目标函数,也考虑了约束条件,比如上面那个函数,加进去就变为:
这里可以看到与α1,α2相乘的部分都为0,所以α1,α2的取值为全体实数。现在这个优化目标函数就没有约束条件了吧,既然如此,求法就简单了,分别对x求导等于0,如下:
把它在带到约束条件中去,可以看到,2个变量两个等式,可以求解,最终可以得到α1=−0.39,α2=−1.63,这样再带回去求x就可以了。那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。那么更高一层的,带有不等式的约束问题怎么办?那么就需要用更一般化的拉格朗日乘子法即KKT条件来解决这种问题了。
二、KKT条件
继续讨论关于带等式以及不等式的约束条件的凸函数优化。任何原始问题约束条件无非最多3种,等式约束,大于号约束,小于号约束,而这三种最终通过将约束方程化简化为两类:约束方程等于0和约束方程小于0。再举个简单的方程为例,假设原始约束条件为下列所示:
那么把约束条件变个样子:
现在将约束拿到目标函数中去就变成:
那么KKT条件的定理是什么呢?就是如果一个优化问题在转变完后变成
其中g是不等式约束,h是等式约束(像上面那个只有不等式约束,也可能有等式约束)。那么KKT条件就是函数的最优值必定满足下面条件:
(1) L对各个x求导为零;
(2) h(x)=0;
(3) ∑αigi(x)=0,αi≥0
这三个式子前两个好理解,重点是第三个式子不好理解,因为我们知道在约束条件变完后,所有的g(x)<=0,且αi≥0,然后求和还要为0,无非就是告诉你,要么某个不等式gi(x)=0,要么其对应的αi=0。那么为什么KKT的条件是这样的呢?
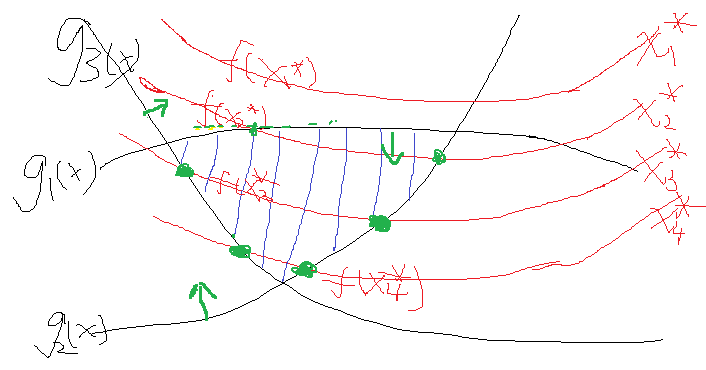
假设就这么几个吧,最终约束是把自变量约束在一定范围,而函数是在这个范围内寻找最优解。函数开始也不知道该取哪一个值是吧,那就随便取一个,假设某一次取得自变量集合为x1*,发现一看,不满足约束,然后再换呀换,换到了x2*,发现可以了,但是这个时候函数值不是最优的,并且x2*使得g1(x)与g2(x)等于0了,而g3(x)还是小于0。这个时候,我们发现在x2的基础上再寻找一组更优解要靠谁呢?当然是要靠约束条件g1(x)与g2(x),因为他们等于0了,很极限呀,一不小心,走错了就不满足它们两了,这个时候我们会选择g1(x)与g2(x)的梯度方向往下走,这样才能最大程度的拜托g1(x)与g2(x)=0的命运,使得他们满足小于0的约束条件对不对。至于这个时候需不需要管g3(x)呢?正常来说管不管都可以,如果管了,也取g3在x2*处的梯度的话,因为g3已经满足了小于0的条件,这个时候在取在x2*处的梯度,你能保证它是往好的变了还是往差的变了?答案是都有可能。运气好,往好的变了,可以更快得到结果,运气不好,往差的变了,反而适得其反。那么如果不管呢?因为g1(x)与g2(x)已经在边缘了,所以取它的梯度是一定会让目标函数变好的。综合来看,这个时候我们就不选g3。那么再往下走,假设到了自变量优化到了x3*,这个时候发现g2(x)与g3(x)等于0,也就是走到边了,而g1(x)小于0,可变化的空间绰绰有余,那么这个时候举要取g2(x)与g3(x)的梯度方向作为变化的方向,而不用管g1(x)。那么一直这样走呀走,最终找到最优解。可以看到的是,上述如果g1(x)、g2(x)=0的话,我们是需要优化它的,又因为他们本身的条件是小于0的,所以最终的公式推导上表明,是要乘以一个正系数α作为他们梯度增长的倍数,而那些不需要管的g(x)为了统一表示,这个时候可以将这个系数设置为0,那么这一项在这一次的优化中就没有了。那么把这两种综合起来就可以表示为
∑αigi(x)=0,αi≥0。
也即是某次的g(x)在为最优解起作用,那么它的系数值(可以)不为0。如果某次g(x)没有为下一次的最优解x的获得起到作用,那么它的系数就必须为0,这就是这个公式的含义。
比如上面例子的目标值与约束:
此时分别对x1、x2求导数:
而我们还有一个条件就是α∗g(x)=0,那么也就是:
这样我们就去讨论下,要么g=0,要么α=0,这里两个g两个α,这样我们就需要讨论四种情况,可能你会说,这是约束条件少的情况,那么如果有10个约束条件,这样就有10个g和10个α,你去给我讨论?多少种组合,不知道,但是换个思路,我们非得去10个一起去讨论?机智的学者想到一种方法,考虑到∑αigi(x)=0这个条件,那么我两个两个讨论不就可以了,比如现在我就讨论α7,α8,让其他的α不变,为什么选或者至少选两个讨论呢,因为这个式子求和为0,改变一个显然是不行的,那就改变两个,你增我就减,这样和可以为0。再问为什么不讨论3个呢?也可以,这不是麻烦嘛,一个俗语怎么说来着,三个和尚没水喝,假设你改变了一个,另外两个你说谁去减或者加使得和为0,还是两个都变化一点呢?不好说吧,自然界都是成双成对的才和谐,没有成三成四的(有的话也少)。这里顺便提一下后面会介绍到的内容,就是实现SVM算法的SMO方法,在哪里,会有很多α,那么人们怎么解决的呢,就是随便选择两个α去变化,看看结果好的话,就接受,不好的话就舍弃在选择两个α,如此反复,后面介绍。
说回来,这里有四种情况,正好两个α,也不用挑不用减的,一次完事。那么我们分着讨论吧,
(1)α1=α2=0,那么看上面的关系可以得到x1=1,x2=−1,再把两个x带到不等式约束,发现第一个就是需要满足(10-1+20=29<0)显然不行,29>0的。舍弃
(2)g1(x)=g2(x)=0,带进去解得,x1=110/101;x2=90/101,再带回去求解α1,α2α1,α2,发现α1=58/101,α2=4/101,它们满足大于0的条件,那么显然这组解是可以的。
(3)其他两种情况再去讨论发现是不行的。
可以看到像这种简单的讨论完以后就可以得到解了。
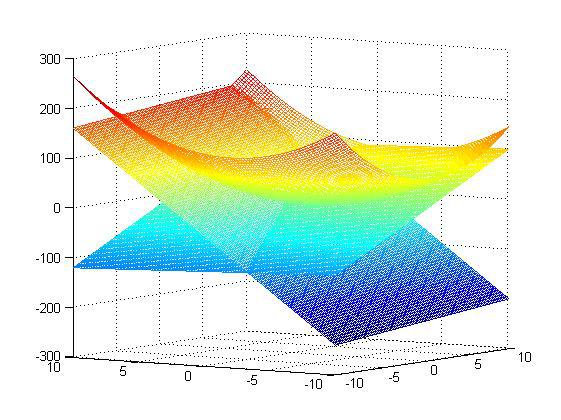
x1=110/101=1.08;x2=90/101=0.89,那么它得到结果对不对呢?这里因为函数简单,可以在matlab下画出来,同时约束条件也可以画出来,那么原问题以及它的约束面画出来就如下所示:
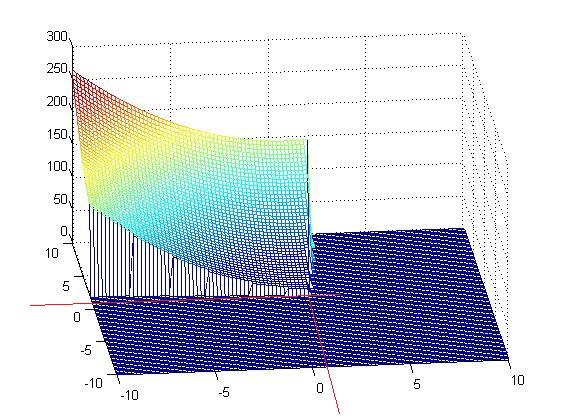
这是截取下来的符合约束要求的目标面
可以看到最优解确实就是上面我们求的那个解。既然简单的问题可以这样解,那么复杂一点的只需要简单化,照样可以解,至此KKT条件解这类约束性问题就是这样,它对后续的SVM求解最优解至关重要。
三、SVM理论基础
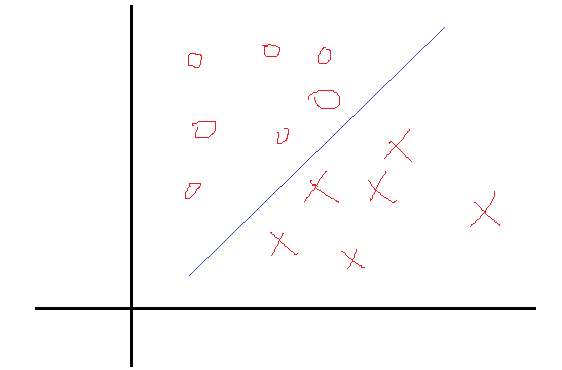
一个简单的二分类问题如下图:
我们希望找到一个决策面使得两类分开,这个决策面一般表示就是WTX+b=0,现在的问题是找到对应的W和b使得分割最好。
那么SVM的求优方式是怎样的呢?
假设我们知道了结果,就是上面这样的分类线对应的权值W和b。那么我们会看到,在这两个类里面,是不是总能找到离这个线最近的点,向下面这样:
然后定义一下离这个线最近的点到这个分界面(线)的距离分别为d1,d2。那么SVM找最优权值的策略就是,先找到最边上的点,再找到这两个距离之和D,然后求解D的最大值,想想如果按照这个策略是不是可以实现最优分类,是的。好了还是假设找到了这样一个分界面WTX+b=0,那么做离它最近的两类点且平行于分类面,如上面的虚线所示。好了再假设我们有这两个虚线,那么真实的分界面我们认为正好是这两个分界面的中间线,这样d1就等于d2了。因为真实的分界面为WTX+b=0WTX+b=0,那么就把两个虚线分别设置为WTX+b=1和WTX+b=−1可以看到虚线相对于真实面只是上下移动了1个单位距离,可能会说你怎么知道正好是一个距离?确实不知道,就假设上下是k个距离吧,那么假设上虚线现在为WTX+b=k,两边同时除k可以吧,这样上虚线还是可以变成WT1X+b1=1,同理下虚线也可以这样,然后他们的中线就是WT1X+b1=0吧,可以看到从k到1,权值无非从w变化到w1,b变到b1,我在让w=w1,b=b1,不是又回到了起点吗,也就是说,这个中间无非是一个倍数关系。所以我们只需要先确定使得上下等于1的距离,再去找这一组权值,这一组权值会自动变化到一定倍数使得距离为1的。
好了再看看D=d1+d2怎么求吧,假设分界面WTX+b=0,再假设X是两维的,那么分界面再细写出来就是:w1x1+w2x2+b=0。上分界线:w1x1+w2x2+b=1,这是什么,两条一次函数(y=kx+b)的曲线是不是,那么初中就学过两直线的距离吧,
这里W=(w1,w2),是个向量,||W||为向量的距离,那么||W||2=WTW。下界面同理。
要使D最大,就要使分母最小,这样优化问题就变为min(WTW),乘一个系数0.5没影响,但是在后面却有用。
我们知道,如果一个一次函数分界面为WTX+b=0,那么线上方的x可以使得WTX+b>0,下方的x可以使得WTX+b<0吧,那么对于上界面以上的点就有WTX+b>1,下界面以下的点就有WTX+b<−1。我们现在再假设上界面以上的点的分类标签为1,下界面以下的点的分类标签为-1。那么这两个不等式再分别乘以他们的标签会怎么样?是不是可以统一为yi(WTxi+b)≥1了(这也是为什么SVM在使用之前为什么要把两类标签设置为+1,-1,而不是0,1等等之类的了)。好了假设分界面一旦确定,是不是所有点都得满足这个关系。那么最终的带约束的优化问题转化为:
把约束条件换成小于号的形式:
注意的是这可不是一个约束条件,而是对所有的每个样本xi都有一个这样的约束条件。
转换到这种形式以后是不是很像上节说到的KKT条件下的优化问题了,就是这个。但是有一个问题,我们说上节的KKT是在凸函数下使用的,那么这里的目标函数是不是呢?答案是的,想想WT∗W,函数乘出来应该很单一,不能有很多极点,当然也也可以数学证明是的。
好了那样的话就可以引入拉格朗日乘子法了,优化的目标变为:
然后要求这个目标函数最优解,求导吧,
这两个公式非常重要,简直是核心公式。
求导得到这个应该很简单吧,那我问你为什么WTW对w求导是w呢?如果你知道,那么你很厉害了,反正开始我是一直没转过来。其实说起来也很简单,如果光去看看为什么求导以后,转置就没了,不太好想明白,设想一下假设现在是二维样本点,也就是最终的W=(w1,w2),那么WTW=w1∗w1+w2∗w2那么对w1求导就是2w1,对w2就是2w2,这样写在一起就是对w求导得到(2w1,2w2)=2w了,然后乘前面一个1/2(这也就是为什么要加一个1/2),就变成w了。
好了得到上面的两个公式,再带回L中把去w和b消掉,你又可能发现,w确实可以消,因为有等式关系,那b怎么办?上述对b求导的结果竟然不含有b,上天在开玩笑吗?其实没有,虽然没有b,但是有那个求和为0呀,带进去你会惊人的发现,b还真的可以消掉,就是因为了那个等式。简单带下:
那么求解最最开始的函数的最小值等价到这一步以后就是求解W的最大值了,因为使用了拉格朗日乘子法后,原问题就变为其对偶问题了,最小变成了最大,至于为什么,等到详细研究过对偶问题再来解释吧。不了解的,只需要知道求W的极值即可。
整理一下,经过这么一圈的转化,最终的问题为:
那么求解最最开始的函数的最小值等价到这一步以后就是求解W的最大值了,因为使用了拉格朗日乘子法后,原问题就变为其对偶问题了,最小变成了最大,至于为什么,等到详细研究过对偶问题再来解释吧。不了解的,只需要知道求W的极值即可。
整理一下,经过这么一圈的转化,最终的问题为:
为什么有αi≥0,这是上节说到的KKT条件的必须。至此问题来源部分到这。
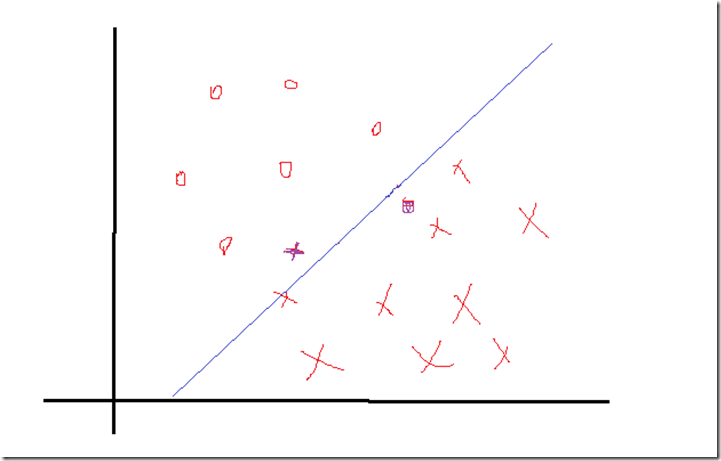
细心的你肯可能会发现,上述所有的构造等等都是在数据完全线性可分,且分界面完全将两类分开,那么如果出现了下面这种情况:
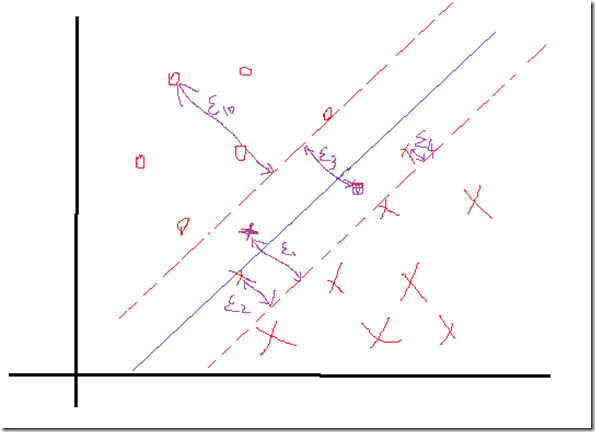
正负两类的最远点没有明显的分解面,搞不好正类的最远点反而会跑到负类里面去了,负类最远点跑到正类里面去了,要是这样的话,你的分界面都找不到,因为你不可能找到将它们完全分开的分界面,那么这些点在实际情况是有的,就是一些离群点或者噪声点,因为这一些点导致整个系统用不了。当然如果不做任何处理确实用不了,但是我们处理一下就可以用了。SVM考虑到这种情况,所以在上下分界面上加入松弛变量ϵi,认为如果正类中有点到上界面的距离小于ϵi,那么认为他是正常的点,哪怕它在上界面稍微偏下一点的位置,同理下界面。还是以上面的情况,我们目测下的是理想的分解面应该是下面这种情况:
如果按照这种分会发现4个离群点,他们到自己对应分界面的距离表示如上,理论上讲,我们给每一个点都给一个自己的松弛变量ϵi,如果一个分界面求出来了,那么比较这个点到自己对应的界面(上、下界面)的距离是不是小于这个值,要是小于这个值,就认为这个界面分的可以,比如上面的ϵ3这个点,虽然看到明显偏离了正轨,但是计算发现它的距离d小于等于我们给的ϵ3,那么我们说这个分界面可以接受。你可能会说那像上面的ϵ10,距离那么远了,他肯定是大于预设给这个点的ϵi了对吧,确实是这样的,但是我们还发现什么?这个点是分对了的点呀,所以你管他大不大于预设值,反正不用调整分界面。需要调整分界面的情况是只有当类似ϵ3这样的点的距离大于了ϵ3的时候。
好了那么因为松弛变量的加入,导致每个点的约束条件就变化了点,像上界面以上的点,它满足的条件可能就是:WTxi+b≥1−ϵi,yi=1
而下界面可能就是:WTxi+b≤−1+ϵi,yi=−1
并且ϵi≥0
统一在一起,整个问题就变成:
你发现目标函数里面多了一点东西,而加上这个是合理的,我们在优化的同时,也使得总的松弛变量之和最小。常数C决定了松弛变量之和的影响程度,如果越大,影响越严重,那么在优化的时候会更多的注重所有点到分界面的距离,优先保证这个和小。
好了将问题写在一起吧:
然后对w,b,ϵ分别求导数:
观察第三个式子,因为ri≥0,所以c−αi≥0⇒αi≤C,结合αi≥0那么0≤αi≤C,把这三个导数结果带到目标函数中去消掉对应的w,b以及ri,你会惊人的发现,连ϵi也消掉了,并且目标函数和没有加松弛变量的一模一样:
这么说,溜了一圈下来,无非多了个αi≤C,其他的什么也没有变,真好。那么统一一下,更一般的带松弛变量的优化函数以及约束条件就变为:
剩下的问题是怎么去找这样一组最优解αi了。看过上节的可能会知道,在上节的最后那个实例中也是寻找αi,不过那里只有两个αi,而αi要么等于0,要么大于0,而αi大于0的时候,对应的另外一个因子就等于0。然后讨论这四种情况找到满足解。但是我们这里的αi可不止2个,想挨着讨论是不行的,且这里的KKT条件和上节的那个还不太一样。那么这里的KKT条件是什么呢?具体又要怎么解这样一堆αi的问题呢?请看下节的SMO算法求解SVM问题。
SMO算法原理
解SVM问题最终演化为求下列带约束条件的问题:
问题的解就是找到一组αi=(α1,α2,...,αn)使得W最小。
现在我们来看看最初的约束条件是什么样子的:
这是最初的一堆约束条件吧,现在有多少个约束条件就会有多少个αi。那么KKT条件的形成就是让
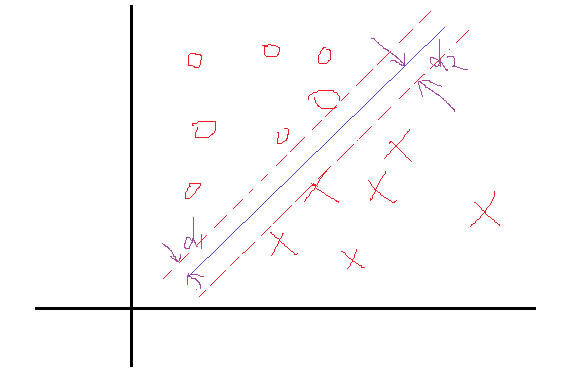
我们知道αi≥0,而后面那个小于等于0,所以他们中间至少有一个为0(至于为什么要这么做,第一节讨论过)。再简单说说原因,假设现在的分类问题如下:
某一次迭代后,分类面为粗蓝线所示,上下距离为1的分界面如细蓝线所示,而理想的分界面如紫虚线所示。那么我们想想,要想把粗蓝线变化到紫虚线,在这一次是哪些个点在起作用?很显然是界于细蓝线边上以及它们之间的所有样本点在起作用吧,而对于那些在细蓝线之外的点,比如正类的四个圈和反类的三个叉,它们在这一次的分类中就已经分对了,那还考虑它们干什么?所以这一次就不用考虑这些分对了的点。那么我们用数学公式可以看到,对于在这一次就分对了的点,它们满足什么关系,显然yi(Wxi+b)>1,然后还得满足αi(1−yi(Wxi+b))=0,那么显然它们的αi=0。对于那些在边界内的点,显然yi(Wxi+b)≤1,而这些点我们说是要为下一次达到更好的解做贡献的,那么我们就取这些约束条件的极限情况,也就是yi(Wxi+b)=1,在这些极限约束条件下,我们就会得到一组新的权值W与b,也就是改善后的解。那么既然这些点的yi(Wxi+b)=1,那它对应的αiαi就可以不为0了,至于是多少,那就看这些点具体属于分界面内的什么位置了,偏离的越狠的点,我想它对应的αiαi就越大,这样才能把这个偏得非常狠的点给拉回来,或者说使其在下一次的解中更靠近正确的分类面。
好了这就是KKT为什么要这么做的原因。那么整理一下,最终带松弛变量的KKT条件就如下所示:
那么满足KKT条件的,我们说如果一个点满足KKT条件,那么它就不需要调整,一旦不满足,就需要调整。由上可知,不满足KKT条件的也有三种情况:
这三种条件下的α都需要调整。那么怎么调整呢?比如说某一次迭代完后发现有10个点不满足,也就是有10个α需要调整,那么10个α在一起,你怎么知道去增加或者减少哪一个或者哪几个α呢?这个时候SMO采取的策略是选择这10个中的两个α出来,就假设为α1,α2吧,调整它们。看看前面有一个条件∑αiyi=0,所以在调整前后满足:
至于ϵ是多少,管它多少,又不用它。也就是说我们只要知道了α1,α2中一个调整以后的值,根据条件另一个值不用算就知道。那么怎么求呢?假设我们来求α2吧。观察上面那个等式,y1,y2是标签,要么1要么-1。而两个α>=0。所以新的α是有范围的。假设现在y1=y2=1或−1,先=1吧,那么αnew1+αnew2=αold1+αold2=ϵ
因为αnew1是在0-C之间,所以假设αnew1=0,那么αnew2可以取到最大值为ϵ,也就是αold1+αold2。而αnew2又不能大于C,所以其最大取值为min(C,αold1+αold2)。同理如果αnew1=C,那么αnew2可以取到最小值为ϵ−C,也就是αold1+αold2−C,而αnew2最小不能小于0,那玩意这个值比0小怎么办?所以αnew2的下限值就为max(0,αold1+αold2−C)。这是相等取1,那么相等取-1呢?同理吧,不过是
−αnew1−αnew2=−αold1−αold2=ϵ两边乘以-1,就是αnew1+αnew2=αold1+αold2=−ϵ,因为你也不知道−ϵ是多少,不过一个字母而已,那么用ϵ代替−ϵ吧,接下来的讨论过程一模一样。从而属于同类别的时候αnew2上下限就有了。同理去计算下不同类(1,-1)的时候的上下限。最终也能得到一个类似的结果,这里就省了,给出最后的结果:
到这只是给出了αnew2的范围,那么它怎么解呢?解这个复杂一点,这里引用牛人博客里的证明。然后只给出一个解的思想。首先我们只想考虑α1,α2,而原问题:
里面有所有的α,这里把这个式子乘开,把含有α1,α2都单独拿出来,其他的作为一堆,就变成下面这样:
v是一个与α1,α2,y1,y2有关的长式子,K是<x1∗x2.>内积。可以看到后面一堆与α1,α2就没有关系。然后因为
这个关系,又可以把α1给消掉是不是,这样新的W前面一部分只与α2有关,后面一部分因为不含α1,α2α1,α2所以与之没关系。而里面的αold1,αold2是上一次迭代的结果,是知道的。这样这个式子对α2求导再等于0,就可以解出α2了,应该是αnew2。(上面那个索引有详细的推导过程)。那么思路就是这样的,最终得到的结果为:
好简单的式子,然后看看αnew2的大小是否符合上面求出来的范围,超出了将其限制在范围内。
有了αnew2,再根据
因为αnew2已经限制范围,而这个范围就是已经认为αnew1的范围属于0-C下而来的,所以αnew1的范围一定是在0-C之间的,对于αnew1就不需要限制范围了。