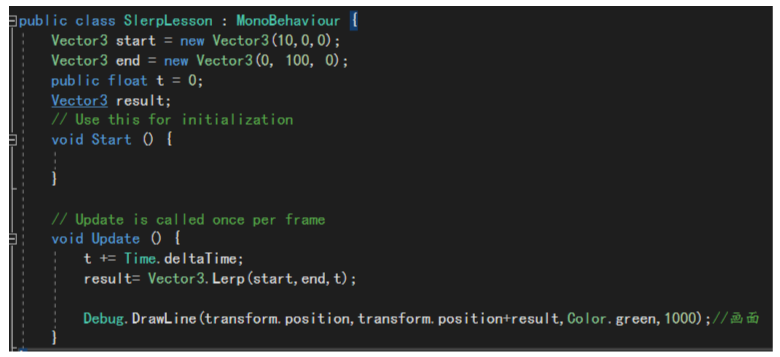
向量*标量
公式:A[x,y,z] *a=[ax,ay,az]
几何意义
- 向量*正数:方向不变,放大模长
- 向量*负数:方向相反,放大模长
- 向量*0:得到零向量
向量点乘
公式
A[x1,y1,z1]
B[x2,y2,z2]
A·B=x1*x2+y1*y2+z1*z2
几何意义
只有向量点乘向量才有意义
A·B=|A|*|B|*cosθ==》cosθ=(A·B)/(|A|*|B|)==》θ=arccos((A·B)/(|A|*|B|))==》θ=arccos(A·B)(条件:A和B单位向量)
用途
计算两个向量的夹角,判断两个向量的方向
Vector3.Angle
直接计算两个向量的夹角,不需要归一化,返回值是角度
向量叉乘
公式
A[x1,y1,z1]
B[x2,y2,z2]
[x3,y3,z3]
- x3=y1*z2-y2*z1
- y3=z1*x2-x1*z2
- z3=x1*y2-x2*y1
几何意义
A×B得到的向量同时垂直于A与B ,A×B向量垂直于A与B组成的平面,即求出的是垂直于AB组成平面的法线
使用左手定则判断法线的方向
线性插值(Vector3.Lerp)
在向量的三个方向上进行Mathf.Lerp
对位置进行差值
变速
t不变,改变Start的值
移动速度先快后慢,位置无限接近,但不会得到end位置
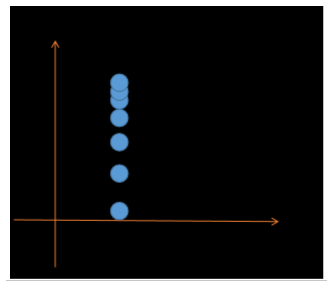
匀速
移动速度均匀,位置每帧接近,当t>=1时,得到end的结果
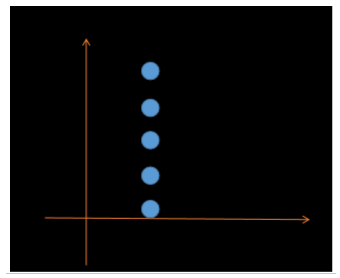
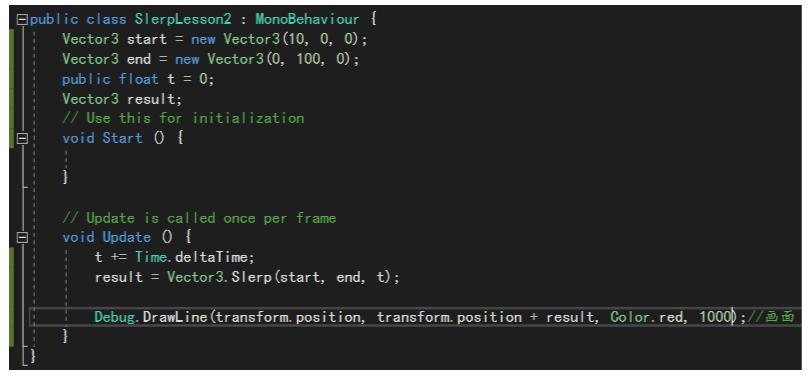
球形差值(Vector3.Slerp)
对向量进行差值,在起点和重点模长相同的情况下,保证模长不变