Description
Tweetuzki 所在的班级有 (n) 名学生,座号从 (1) 到 (n)。有一次,教官命令班上的 (n) 名学生按照座号顺序从左到右排成一排站好军姿,其中 (1) 号学生在最左边,(n) 号学生在最右边。
由于同学们站了很久,怨声载道,仁慈的教官又不希望大家一起解散导致混乱的局面,于是想了一个办法:教官从最左边——也就是 (1) 号学生身旁出发,走到 (n) 号学生右边后,再折返回到 (1) 号同学旁边。在教官在从 (1) 号同学走到 (n) 号同学这段路上,当走到某位同学身边时,他可以选择让这位同学出列,也可以等到折返的时候再使这名同学出列。
但是有一些同学在军训过程中表现极坏,因此教官希望他们晚一些出列休息。对于 (i) 号同学,定义他的“坏值”为 (w_i)。教官希望在一次往返过程中,使得所有学生出列,且最大化 (sum_{i=1}^{n}~r_i~ imes~w_i) 的值,其中 (r_i) 表示 (i) 号同学是第 (r_i) 位出列的学生。机智的教官一下子就想出了这个方案,Tweetuzki 大为惊讶,于是他去请教教官如何做到。可是他的胆子很小而且“坏值”很大,教官可能不会告诉他,所以他就找到了你。
Input
第一行一个整数 (n) 代表序列长度
第二行是 (n) 个整数代表这个序列
Output
第一行一个整数,代表最大坏值
下面一行是 (n) 个数,按照出列选手字典序最小输出坏值
Hint
(0~leq~n,w_i~leq~10^6)
Solution
考虑答案的出列编号序列一定是单峰的,即如果把序列下标作为 (x) 坐标, 出列选手的序号作为 (y) 坐标,则函数图像一定如下
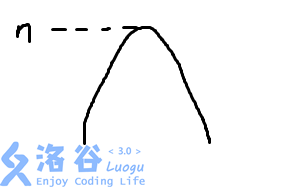
并且 (n) 一定是峰。于是考虑倒着往前决定出队的顺序,考虑已经决定了 (i+1~sim~n)的出队顺序,那么 (i) 只可能放在这条函数图线的最左侧或者最右侧,我们比较他们的贡献。
考虑 (i) 放在最左侧的情况,这相当于他后面出队所有人的 (r) 值都加一,于是放在左侧的贡献 (s_l~=~sum_{j~=i+1}^{n}~w_j~+~w_i)
同理,考虑放在右侧的贡献,即为他前面已经放的人的个数,即 (s_r~=~(n-i)~ imes~w_i~+~w_i)
比较 (sl) 和 (s_r) 的大小即可。由于序号字典序尽可能小,当两者相等时优先放在左侧即可。
Code
#include <cstdio>
#include <vector>
#include <algorithm>
#ifdef ONLINE_JUDGE
#define putchar(o)
puts("I am a cheater!")
#define freopen(a, b, c)
#endif
#define rg register
#define ci const int
#define cl const long long
typedef long long int ll;
namespace IPT {
const int L = 1000000;
char buf[L], *front=buf, *end=buf;
char GetChar() {
if (front == end) {
end = buf + fread(front = buf, 1, L, stdin);
if (front == end) return -1;
}
return *(front++);
}
}
template <typename T>
inline void qr(T &x) {
rg char ch = IPT::GetChar(), lst = ' ';
while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();
while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();
if (lst == '-') x = -x;
}
template <typename T>
inline void ReadDb(T &x) {
rg char ch = IPT::GetChar(), lst = ' ';
while ((ch > '9') || (ch < '0')) lst = ch, ch = IPT::GetChar();
while ((ch >= '0') && (ch <= '9')) x = x * 10 + (ch ^ 48), ch = IPT::GetChar();
if (ch == '.') {
ch = IPT::GetChar();
double base = 1;
while ((ch >= '0') && (ch <= '9')) x += (ch ^ 48) * ((base *= 0.1)), ch = IPT::GetChar();
}
if (lst == '-') x = -x;
}
namespace OPT {
char buf[120];
}
template <typename T>
inline void qw(T x, const char aft, const bool pt) {
if (x < 0) {x = -x, putchar('-');}
rg int top=0;
do {OPT::buf[++top] = x % 10 + '0';} while (x /= 10);
while (top) putchar(OPT::buf[top--]);
if (pt) putchar(aft);
}
const int maxn = 1000010;
int n;
ll ans, sum;
int MU[maxn], temp[maxn];
std::vector<int>pre,pos;
int main() {
freopen("1.in", "r", stdin);
qr(n);
for (rg int i = 1; i <= n; ++i) qr(MU[i]);
for (rg int i = n; i; --i) {
ll sl = sum + MU[i], sr = 1ll * MU[i] * (n - i) + MU[i];
if (sl >= sr) {pre.push_back(i); ans += sl;}
else {pos.push_back(i); ans += sr;}
sum += MU[i];
}
qw(ans, '
', true);
int sz = pre.size();
for (rg int i = sz - 1; ~i; --i) qw(MU[pre[i]], ' ', true);
sz = pos.size();
for (rg int i = 0; i < sz; ++i) qw(MU[pos[i]], ' ', true);
putchar('
');
}