【DP】【CF1097D】 Makoto and a Blackboard

更好的阅读体验

Description

给定一个数 (n)，对它进行 (k) 次操作，每次将当前的数改为自己的因数，包括 (1) 和自己。写出变成所有因数的概率是相等的。求 (k) 次以后 (n) 期望会变成多少

Input

一行两个整数 (n,k)

Output

一行一个整数代表答案

Hint

(1~leq~n~leq~10^{15}~,~1~leq~k~leq~10^4)

Solution

Hello 2019！

我们考虑整个数字变化的树形图：

以 (n~=~6~,~k~=~2) 为例：

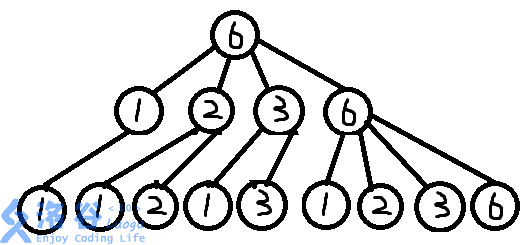
（恕我直言，这图是真的丑）

然后我们将这张图改一下，要求每个非叶节点都有 (4) 个孩子，如果孩子数不足，就让他们平分这四个。于是新的变化图如下：

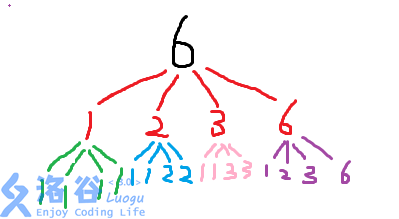
（恕我直言，这图更丑了）

我们发现这张图上所有叶节点出现的概率都是等可能的，并且他们包含了所有的情况，所以求出这些数字的和再除以节点数就是期望值。

接着考虑由于一个数字的所有质因数都是独立的，同时每个质因子都可以画出类似的转移图，依据唯一分解定理，我们可以将质因子拆开，对于每个质因子求出他们期望变成多少，然后乘起来即为总期望。这里的质因子包括了质数 (p) 和它的指数 (c)。

接着考虑我们对质因子DP。一次对 (p^c) 的操作相当于将其变成 (p^0,p^1,p^2,dots p^c) 中的任意一个。于是我们可以将一次操作转化成将指数 (c) 变成 ([1,c]) 中任意一个数。我们规定任何一个节点都有 (d(n)) 个孩子， (d(n)) 为 (n) 的因数个数。则对于一个数值为 (x) 的节点，她有 (frac{1}{x + 1}) 的概率变成 (y~(0~leq~y~leq~x))，那么它会占据 (x) 的 (frac{d(n)}{x + 1}) 个孩子。

例如，对于 (2^2) 进行 (2) 次变化的指数图如下

我们认为粉色的位置每个数占据了 (frac{1}{2}) 个儿子

于是我们考虑当我们进行了 (i) 次变化，第 (w) 个质因子在树形图上的第 (i) 层指数数值为 (j) 的节点个数，则显然有

[f_{w,i,j}~=~sum_{h = j}^{c_w}~f_{w,i - 1,h}~ imes~frac{d(n)}{h + 1} ]

其中 (c_j) 为 (n) 的唯一分解式中对应项的指数。

于是我们枚举 (n) 的因数，求出他们出现的次数与他们值的乘积，除以最下面一层的节点个数即为答案

[egin{aligned}ans~& =~frac{1}{d^k(n)}~sum_{x mid n}~Times_d~ imes~x\&=frac{1}{d^k(n)}~sum_{x mid n}~d~prod_{i = 1}^{d(n)}~f_{i,k,h}end{aligned} ]

其中 (h) 为 (d) 唯一分解式对应项的指数。

我们发现在 DP时，第 (k) 层每个位置都被乘了 (d^k(n))，于是可以和式子中的 (frac{1}{d^k(n)}) 约掉，式子变为

[f_{w,i,j}~=~sum_{h = j}^{c_w}~f_{w,i - 1,h}~ imes~frac{1}{h + 1} ]

[egin{aligned}ans~& =~sum_{x mid n}~Times_d~ imes~x\&=~sum_{x mid n}~d~prod_{i = 1}^{d(n)}~f_{i,k,h}end{aligned} ]

看起来舒服多了。

考虑复杂度：我们枚举了 (k) 层，每层枚举了 (n) 的质因数个数次，这里的质因数不包括指数，但是包括重复的，例如 (p^2) 算作两个质因数。由于一个数 (n) 的质因数为 (O(log n))，所以总状态复杂度为 (O(k log n))。在转移时，我们枚举的上界是 (O(log n))，所以总复杂度为 (O(k~log^2 n))。发现转移的位置事实上转移了一个加权后缀和，于是我们再开一个数组维护这个后缀和即可做到 (O(k log n))。

注意到这样会爆空间，但是发现对于每个DP状态我们只需要第 (k) 层的情况，并且第一维互不影响，于是我们可以把第一维省掉，每次DP完一个质因子用另一个数组记录第 (k) 层的答案，即可做到空间复杂度 (O(log^2 n~+~k~log n))。（其实动态开DP数组可以做到空间复杂度 (O(k~log n))，但是没啥意义）

最后统计答案时直接爆搜因数即可。

Code

#include <cstdio>
#include <cstring>
#include <vector>
#ifdef ONLINE_JUDGE
#define freopen(a, b, c)
#endif
#define rg register
#define ci const int
#define cl const long long

typedef long long ll;

namespace IPT {
    const int L = 1000000;
    char buf[L], *front=buf, *end=buf;
    char GetChar() {
	    if (front == end) {
		    end = buf + fread(front = buf, 1, L, stdin);
		    if (front == end) return -1;
		}
	    return *(front++);
	}
}

template <typename T>
inline void qr(T &x) {
    rg char ch = IPT::GetChar(), lst = ' ';
    while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();
    while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();
    if (lst == '-') x = -x;
}

template <typename T>
inline void ReadDb(T &x) {
    rg char ch = IPT::GetChar(), lst = ' ';
    while ((ch > '9') || (ch < '0')) lst = ch, ch = IPT::GetChar();
    while ((ch >= '0') && (ch <= '9')) x = x * 10 + (ch ^ 48), ch = IPT::GetChar();
    if (ch == '.') {
	    ch = IPT::GetChar();
	    double base = 1;
	    while ((ch >= '0') && (ch <= '9')) x += (ch ^ 48) * ((base *= 0.1)), ch = IPT::GetChar();
	}
    if (lst == '-') x = -x;
}

namespace OPT {
    char buf[120];
}

template <typename T>
inline void qw(T x, const char aft, const bool pt) {
    if (x < 0) {x = -x, putchar('-');}
    rg int top=0;
    do {OPT::buf[++top] = x % 10 + '0';} while (x /= 10);
    while (top) putchar(OPT::buf[top--]);
    if (pt) putchar(aft);
}

const int maxt = 60;
const int maxm = 10010;
const int MOD = 1000000007;

ll n, kk, ans;
ll frog[maxm][maxt], inv[maxt], gorf[maxt][maxt], sum[maxm][maxt];
std::vector<ll> d;
int cnt;
int c[maxt];

void Get_Inv(ci, ci);
void dfs(ci, ci);
int mpow(cl x, int);

signed main() {
    freopen("1.in", "r", stdin);
    qr(n); qr(kk);
    Get_Inv(59, MOD);
    ll dn = n;d.push_back(0);
    for (ll i = 2; (i * i) <= n; ++i) if(!(dn % i)) {
	    d.push_back(i); ++cnt;
	    while (!(dn % i)) {dn /= i; ++c[cnt];}
	}
    if (dn != 1) {++cnt; d.push_back(dn); c[cnt] = 1;}
    for (rg int j = 1; j <= cnt; ++j) {
	    frog[0][c[j]] = sum[0][c[j]] = inv[c[j] + 1];
	    for (rg int i = 0; i < c[j]; ++i) frog[0][i] = 0, sum[0][i] = sum[0][c[j]];
	    for (rg int i = 1; i <= kk; ++i) {
		    rg int di = i - 1;
		    sum[i][c[j] + 1] = 0;
		    for (rg int k = c[j]; ~k; --k) {
			    frog[i][k] = sum[di][k];
			    sum[i][k] = (sum[i][k + 1] + frog[i][k] * inv[k + 1] % MOD) % MOD;
			}
		}
	    for (rg int k = 0; k <= c[j]; ++k) gorf[j][k] = frog[kk][k];
	}
    dfs(1, 1);
    qw((ans + MOD) % MOD, '
', true);
    return 0;
}

void Get_Inv(ci x, ci p) {
    inv[1] = 1;
    for (rg int i = 2; i <= x; ++i) inv[i] = - p / i * inv[p % i] % MOD;
}

void dfs(ci cur, ci v) {
    if (cur > cnt) {ans = (ans + v) % MOD; return;}
    for (int i = 0; i <= c[cur]; ++i) dfs(cur + 1, 1ll * gorf[cur][i] * v % MOD * mpow(d[cur], i) % MOD);
}

int mpow(cl x, int y) {
    ll _ret = 1, _temp = x % MOD;
    while (y) {
	    if (y & 1) _ret = _ret * _temp % MOD;
	    _temp = _temp * _temp % MOD;
	    y >>= 1;
	}
	return _ret;
}