题目链接:http://poj.org/problem?id=1182
搞了好久才弄明白。。。之前学并查集从来没想过能这么用,并查集+向量偏移!!!
与一般并查集只开一个father数组不同,还要开一个ralation数组用来记录子节点与父节点的关系,对于此题,显然每个点对应根节点可能有三种关系,我用ralation[i]=0记为i与根节点是同类,relation[i]=1记为i被根节点吃,relation[i]=2记为i吃根节点。
难点在于合并两个结点时如何更新节点对应的关系值(即relation[i],比如两个节点有不同的父节点,分别对应自己的父节点有一个关系值,而此时这两个点也有关系,需要合并,那么某棵树上的关系值很可能全都要改)。
下面就是合并过程,结合图分析,向量思维。如图:
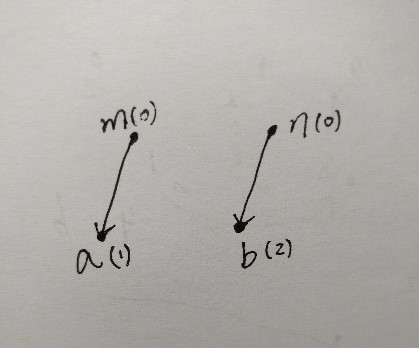
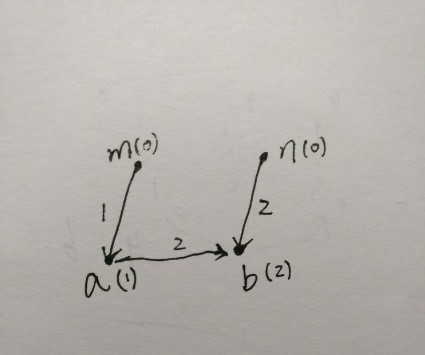
图一 图二
图一:表示m和n分别为两棵树的根节点,对应的关系为0,即与自己是同类。A对m的关系为1,即被m吃,同理b吃n;记向量m->a=1;n->b=2;
图二:加入a和b的关系,a被b吃,即图中的向量a->b=2;此时要合并两棵树,即要求n对m的关系(我们定为n树合到m树),即向量m->n的值。
根据向量的运算法则,m->n = m->a + a->b + b->n = m->a + a->b – n->b
即relation[n]=(relation[a]+(d-1)-relation[b]+3)%3; 括号中加3是为了防止出现负号,对3取模是因为只有0,1,2三种关系。
然后求更新relation[b](即m->b的值)就简单了,还是向量的思想,m->b = m->n +n->b,同上relation[b]=(relation[n]+relation[b])%3; 注意代码中我放到了getfather里面进行这一步。
全部更新完之后图就变成了这样
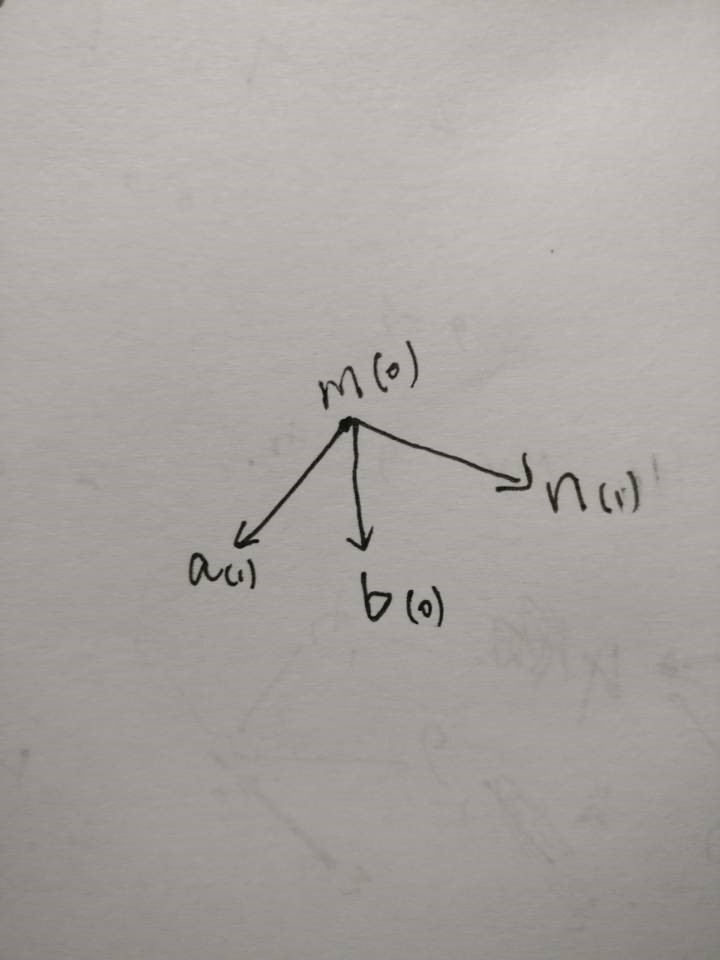
再配合代码看应该就很好理解了。。
1 #include<cstdio> 2 #include<cstring> 3 const int maxn=50010; 4 int f[maxn],r[maxn]; //f[]为父亲数组,r[]为关系数组 5 int n,m,u,v; 6 int d,ans; 7 void init() //初始化 8 { 9 for(int i=1;i<=n;i++) 10 { 11 f[i]=i; 12 r[i]=0; 13 } 14 } 15 16 int gf(int x) //getfather 17 { 18 if(x!=f[x]) 19 { 20 int t=f[x]; 21 f[x]=gf(t); 22 r[x]=(r[x]+r[t])%3; //向量偏移 23 } 24 return f[x]; 25 } 26 27 void uni(int a,int b) //合并 28 { 29 int pa=gf(a); 30 int pb=gf(b); 31 if(pa==pb) 32 { 33 if(d==1&&r[a]!=r[b]) ans++; 34 else if(d==2&&(r[a]+1)%3!=r[b]) ans++; //这点稍微想想就可得到 35 } 36 else { 37 f[pb]=pa; 38 r[pb]=(r[a]+d-1+3-r[b])%3; //向量偏移!!!!! 39 } 40 } 41 42 int main() 43 { 44 scanf("%d%d",&n,&m); //注意此题单组输入,,不是以EOF结束输入。。否则WA!!!!! 45 init(); 46 ans=0; 47 for(int i=0;i<m;i++) 48 { 49 scanf("%d%d%d",&d,&u,&v); 50 if(u>n||v>n) ans++; 51 else if(d==2&&u==v) ans++; 52 else 53 uni(u,v); 54 } 55 printf("%d ",ans); 56 57 }
再看这两道题加以练习巩固。