参考书籍《算法设计与分析》 王晓东 动态规划
1.问题描述
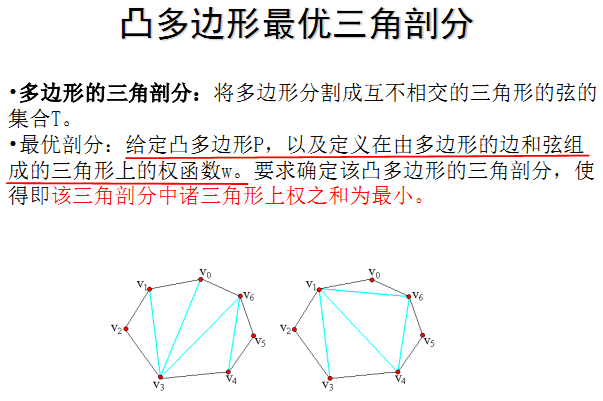
(注:是所有的三角形的权值之和,不是只计算边和弦的权值之和)
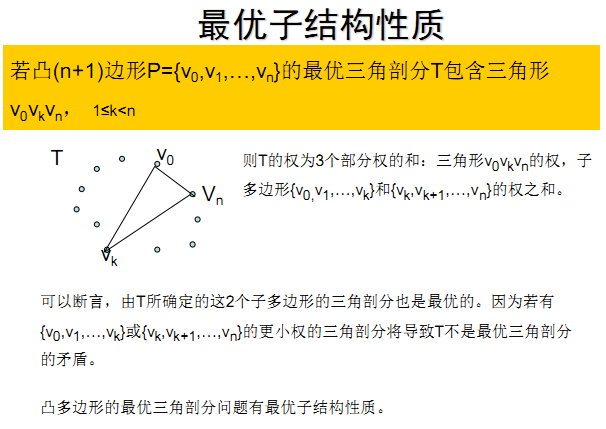
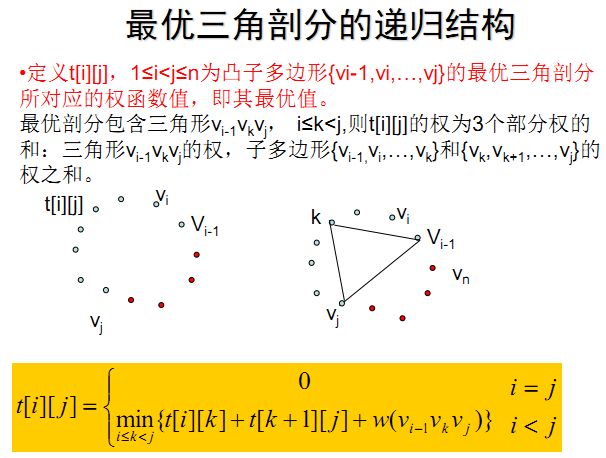
2.分析

3.编码实现:
/**
* @Author:胡家威
* @CreateTime:2011-11-10 下午12:31:16
* @Description:凸多边形的最优三角剖分
*/
package ex2;
public class Triangulation {
private int n;// n多边形
private int[][] weight;// 边的权值数组
public Triangulation(int n) {
this.n = n;
this.weight = new int[n][n];
}
public static void main(String[] args) {
Triangulation triangulation = new Triangulation(6);
initTriangulation(triangulation);
int n = triangulation.getN();// 凸多边形的边数
int[][] t = new int[n][n];// t[i][j]表示顶点{Vi-1,Vi...Vj}组成的多边形的最优三角形剖分的权值
int[][] s = new int[n][n];// s[i][j]表示与Vi-1和Vj一起构成三角形的第三个顶点的位置
triangulation.minWeightTriangulation2(triangulation.getN() - 1, t, s);
System.out.println(t[1][5]);
}
// 初始化weight数组的信息
public static void initTriangulation(Triangulation triangulation) {
int[][] weight = { { 0, 2, 2, 3, 1, 4 }, { 2, 0, 1, 5, 2, 3 }, { 2, 1, 0, 2, 1, 4 },
{ 3, 5, 2, 0, 6, 2 }, { 1, 2, 1, 6, 0, 1 }, { 4, 3, 4, 2, 1, 0 } };
triangulation.setWeight(weight);
}
// 得到最优的三角形剖分,n是总边数-1
public void minWeightTriangulation(int n, int[][] t, int[][] s) {
// 初始化所有的二顶点多边形权值为0
for (int i = 1; i <= n; i++) {
t[i][i] = 0;
}
// 循环求解t[i][j]
for (int r = 2; r <= n; r++) {// (j-i)的范围[2,n]
// 当r=2时,循环实际上是在给t赋边的值,即相邻的两个顶点的权值,例如t[1][2],t[2][3]...
for (int i = 1; i <= n - r + 1; i++) {// i的范围[1,n+1-r],这里i要保证i+r<=n
int j = i + r - 1;
t[i][j] = t[i + 1][j] + getWeight(i - 1, i, j);// 这里实际上就是k=i
// t[i][j] = t[i][i] + t[i + 1][j] + getWeight(i - 1, i, j)
s[i][j] = i;
// i-1,i,j
// 循环k,范围是[i+1,j-1],求出最小的t[i][j]
for (int k = i + 1; k < j; k++) {// k是i和j之间的中间顶点
int u = t[i][k] + t[k + 1][j] + getWeight(i - 1, k, j);// 以k作为划分得到的权值
if (u < t[i][j]) {// 如果权值更小,那么同时更新t[i][j]和s[i][j]
t[i][j] = u;
s[i][j] = k;
}
}
}
}
}
// 我的写法,在第二个循环这里不同,没有什么差别,只是我易于我理解
public void minWeightTriangulation2(int n, int[][] t, int[][] s) {
// 初始化所有的二顶点多边形权值为0
for (int i = 1; i <= n; i++) {
t[i][i] = 0;
}
// 循环求解t[i][j]
for (int r = 1; r <= n; r++) {// r=(j-i)的范围[1,n]
// 当r=1时,循环实际上是在给t赋边的值,即相邻的两个顶点的权值,例如t[1][2],t[2][3],t[3][4]...
for (int i = 1; i <= n - r; i++) {// i的范围[1,n-r],这里i要保证 j=i+r<=n
int j = i + r;
t[i][j] = t[i + 1][j] + getWeight(i - 1, i, j);// 这里实际上就是k=i
// t[i][j] = t[i][i] + t[i + 1][j] + getWeight(i - 1, i, j)
s[i][j] = i;// i-1,i,j
// 循环k,范围是[i+1,j-1],求出最小的t[i][j]
for (int k = i + 1; k < j; k++) {// k是i和j之间的中间顶点
int u = t[i][k] + t[k + 1][j] + getWeight(i - 1, k, j);// 以k作为划分得到的权值
if (u < t[i][j]) {// 如果权值更小,那么同时更新t[i][j]和s[i][j]
t[i][j] = u;
s[i][j] = k;
}
}
}
}
}
// 计算一个三角形的权值之和
public int getWeight(int i, int j, int k) {
return weight[i][j] + weight[j][k] + weight[i][k];
}
public int getN() {
return n;
}
public void setN(int n) {
this.n = n;
}
public int[][] getWeight() {
return weight;
}
public void setWeight(int[][] weight) {
this.weight = weight;
}
}
* @Author:胡家威
* @CreateTime:2011-11-10 下午12:31:16
* @Description:凸多边形的最优三角剖分
*/
package ex2;
public class Triangulation {
private int n;// n多边形
private int[][] weight;// 边的权值数组
public Triangulation(int n) {
this.n = n;
this.weight = new int[n][n];
}
public static void main(String[] args) {
Triangulation triangulation = new Triangulation(6);
initTriangulation(triangulation);
int n = triangulation.getN();// 凸多边形的边数
int[][] t = new int[n][n];// t[i][j]表示顶点{Vi-1,Vi...Vj}组成的多边形的最优三角形剖分的权值
int[][] s = new int[n][n];// s[i][j]表示与Vi-1和Vj一起构成三角形的第三个顶点的位置
triangulation.minWeightTriangulation2(triangulation.getN() - 1, t, s);
System.out.println(t[1][5]);
}
// 初始化weight数组的信息
public static void initTriangulation(Triangulation triangulation) {
int[][] weight = { { 0, 2, 2, 3, 1, 4 }, { 2, 0, 1, 5, 2, 3 }, { 2, 1, 0, 2, 1, 4 },
{ 3, 5, 2, 0, 6, 2 }, { 1, 2, 1, 6, 0, 1 }, { 4, 3, 4, 2, 1, 0 } };
triangulation.setWeight(weight);
}
// 得到最优的三角形剖分,n是总边数-1
public void minWeightTriangulation(int n, int[][] t, int[][] s) {
// 初始化所有的二顶点多边形权值为0
for (int i = 1; i <= n; i++) {
t[i][i] = 0;
}
// 循环求解t[i][j]
for (int r = 2; r <= n; r++) {// (j-i)的范围[2,n]
// 当r=2时,循环实际上是在给t赋边的值,即相邻的两个顶点的权值,例如t[1][2],t[2][3]...
for (int i = 1; i <= n - r + 1; i++) {// i的范围[1,n+1-r],这里i要保证i+r<=n
int j = i + r - 1;
t[i][j] = t[i + 1][j] + getWeight(i - 1, i, j);// 这里实际上就是k=i
// t[i][j] = t[i][i] + t[i + 1][j] + getWeight(i - 1, i, j)
s[i][j] = i;
// i-1,i,j
// 循环k,范围是[i+1,j-1],求出最小的t[i][j]
for (int k = i + 1; k < j; k++) {// k是i和j之间的中间顶点
int u = t[i][k] + t[k + 1][j] + getWeight(i - 1, k, j);// 以k作为划分得到的权值
if (u < t[i][j]) {// 如果权值更小,那么同时更新t[i][j]和s[i][j]
t[i][j] = u;
s[i][j] = k;
}
}
}
}
}
// 我的写法,在第二个循环这里不同,没有什么差别,只是我易于我理解
public void minWeightTriangulation2(int n, int[][] t, int[][] s) {
// 初始化所有的二顶点多边形权值为0
for (int i = 1; i <= n; i++) {
t[i][i] = 0;
}
// 循环求解t[i][j]
for (int r = 1; r <= n; r++) {// r=(j-i)的范围[1,n]
// 当r=1时,循环实际上是在给t赋边的值,即相邻的两个顶点的权值,例如t[1][2],t[2][3],t[3][4]...
for (int i = 1; i <= n - r; i++) {// i的范围[1,n-r],这里i要保证 j=i+r<=n
int j = i + r;
t[i][j] = t[i + 1][j] + getWeight(i - 1, i, j);// 这里实际上就是k=i
// t[i][j] = t[i][i] + t[i + 1][j] + getWeight(i - 1, i, j)
s[i][j] = i;// i-1,i,j
// 循环k,范围是[i+1,j-1],求出最小的t[i][j]
for (int k = i + 1; k < j; k++) {// k是i和j之间的中间顶点
int u = t[i][k] + t[k + 1][j] + getWeight(i - 1, k, j);// 以k作为划分得到的权值
if (u < t[i][j]) {// 如果权值更小,那么同时更新t[i][j]和s[i][j]
t[i][j] = u;
s[i][j] = k;
}
}
}
}
}
// 计算一个三角形的权值之和
public int getWeight(int i, int j, int k) {
return weight[i][j] + weight[j][k] + weight[i][k];
}
public int getN() {
return n;
}
public void setN(int n) {
this.n = n;
}
public int[][] getWeight() {
return weight;
}
public void setWeight(int[][] weight) {
this.weight = weight;
}
}
数据:


结果是: 24