Description
Masha wants to open her own bakery and bake muffins in one of the n cities numbered from 1 to n. There are m bidirectional roads, each of whose connects some pair of cities.
To bake muffins in her bakery, Masha needs to establish flour supply from some storage. There are only k storages, located in different cities numbered a1, a2, ..., ak.
Unforunately the law of the country Masha lives in prohibits opening bakery in any of the cities which has storage located in it. She can open it only in one of another n - k cities, and, of course, flour delivery should be paid — for every kilometer of path between storage and bakery Masha should pay 1 ruble.
Formally, Masha will pay x roubles, if she will open the bakery in some city b (ai ≠ b for every 1 ≤ i ≤ k) and choose a storage in some city s(s = aj for some 1 ≤ j ≤ k) and b and s are connected by some path of roads of summary length x (if there are more than one path, Masha is able to choose which of them should be used).
Masha is very thrifty and rational. She is interested in a city, where she can open her bakery (and choose one of k storages and one of the paths between city with bakery and city with storage) and pay minimum possible amount of rubles for flour delivery. Please help Masha find this amount.
The first line of the input contains three integers n, m and k (1 ≤ n, m ≤ 105, 0 ≤ k ≤ n) — the number of cities in country Masha lives in, the number of roads between them and the number of flour storages respectively.
Then m lines follow. Each of them contains three integers u, v and l (1 ≤ u, v ≤ n, 1 ≤ l ≤ 109, u ≠ v) meaning that there is a road between cities u and v of length of l kilometers .
If k > 0, then the last line of the input contains k distinct integers a1, a2, ..., ak (1 ≤ ai ≤ n) — the number of cities having flour storage located in. If k = 0 then this line is not presented in the input.
Print the minimum possible amount of rubles Masha should pay for flour delivery in the only line.
If the bakery can not be opened (while satisfying conditions) in any of the n cities, print - 1 in the only line.
5 4 2
1 2 5
1 2 3
2 3 4
1 4 10
1 5
3
3 1 1
1 2 3
3
-1
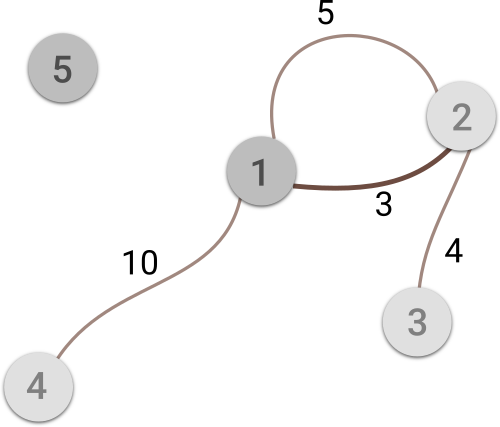
Image illustrates the first sample case. Cities with storage located in and the road representing the answer are darkened.
题意:寻找没有仓库的点到一个仓库的点最短路径
解法:先把图存下来,用数组记录仓库的点(防止例子中出现1 2为仓库,就不能输出3,而应该是4),然后遍历没有仓库的点到仓库点的距离求最小就好了
这里注意输出-1和不连通的情况
#include<bits/stdc++.h>
using namespace std;
string s;
vector<pair<int,int>>mp[100001];
int n,m,k;
int INF=(1<<31)-1;
int inf=(1<<31)-1;
map<int,int>q;
int pos[100001];
int main()
{
int flag=0;
cin>>n>>m>>k;
for(int i=1; i<=m; i++)
{
int a,b,c;
cin>>a>>b>>c;
// INF=min(INF,c);
mp[a].push_back(make_pair(b,c));
mp[b].push_back(make_pair(a,c));
}
for(int i=1; i<=k; i++)
{
cin>>pos[i];
q[pos[i]]=1;
if(mp[pos[i]].empty()==0)
{
flag=1;
}
}
if(k==0||k==n||flag==0)
{
cout<<"-1"<<endl;
}
else
{
for(int i=1; i<=n; i++)
{
int x=pos[i];
for (int j=0; j<mp[x].size(); j++)
{
if(q[mp[x][j].first]==0)
{
inf=min(inf, mp[x][j].second);
}
}
}
if(inf!=(1<<31)-1)
{
cout<<inf<<endl;
}
else
{
cout<<"-1"<<endl;
}
}
return 0;
}