经典排序算法

参考：

https://www.cnblogs.com/chengxiao/p/6262208.html

https://www.cnblogs.com/10158wsj/p/6782124.html?utm_source=tuicool&utm_medium=referral

https://www.cnblogs.com/onepixel/articles/7674659.html

一、各个排序算法复杂度比较

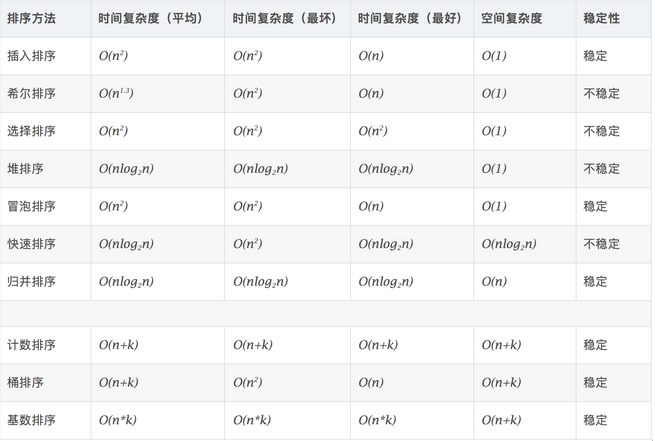
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。

不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。

空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数

二、各个算法的实现及代码

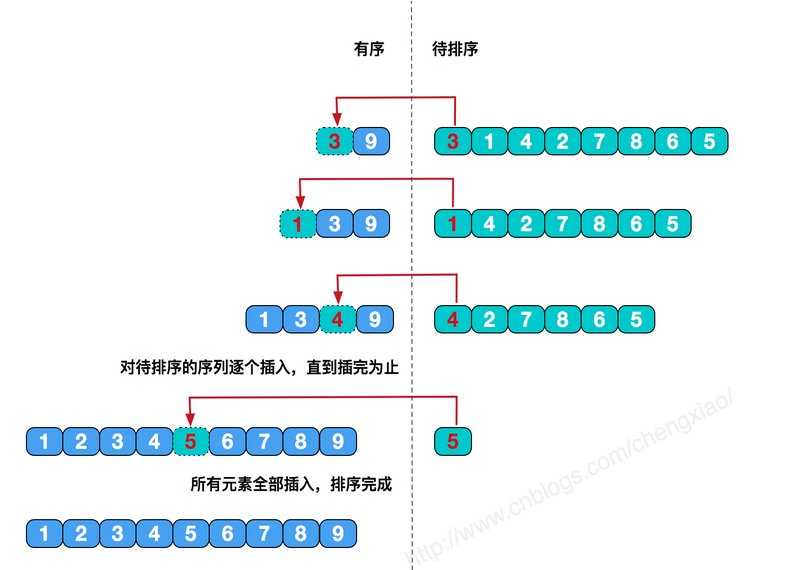
1、直接插入排序（对几乎已经排好序的数据操作是，效率高）

直接插入排序基本思想是：每一步将一个待排序的记录，插入到前面已经排好序的有序序列中去，直到插完所有元素为止

代码部分：

• 设定插入次数，即循环次数，for(int i=1;i<length;i++)，1个数的那次不用插入
• 设定插入数和得到已经排好序列的最后一个数的位数。insertNum和j=i-1
• 从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位。
• 将当前数放置到空着的位置，即j+1

public void insertSort(int [] a){
        int len=a.length;//单独把数组长度拿出来，提高效率
        int insertNum;//要插入的数
        for(int i=1;i<len;i++){//因为第一次不用，所以从1开始
            insertNum=a[i];
            int j=i-1;//序列元素个数
            while(j>=0&&a[j]>insertNum){//从后往前循环，将大于insertNum的数向后移动
                a[j+1]=a[j];//元素向后移动
                j--;
            }
            a[j+1]=insertNum;//找到位置，插入当前元素
        }
    }

2、希尔排序（递减增量排序算法，是插入排序的一种更高效的改进版本）

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率
• 但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位

实现：希尔排序在数组中采用跳跃式分组的策略，通过某个增量将数组元素划分为若干组，然后分组进行插入排序，随后逐步缩小增量，继续按组进行插入排序操作，直至增量为1

public void sheelSort(int [] a){
        int len=a.length;//单独把数组长度拿出来，提高效率
        while(len!=0){
            len=len/2;
            for(int i=0;i<len;i++){//分组
                for(int j=i+len;j<a.length;j+=len){//元素从第二个开始
                    int k=j-len;//k为有序序列最后一位的位数
                    int temp=a[j];//要插入的元素
                    /*for(;k>=0&&temp<a[k];k-=len){
                        a[k+len]=a[k];
                    }*/
                    while(k>=0&&temp<a[k]){//从后往前遍历
                        a[k+len]=a[k];
                        k-=len;//向后移动len位
                    }
                    a[k+len]=temp;
                }
            }
        }
    }

3、简单选择排序（常用于取序列中最大最小的几个数时）

实现：

• 遍历整个序列，将最小的数放在最前面。
• 遍历剩下的序列，将最小的数放在最前面。
• 重复第二步，直到只剩下一个数

public void selectSort(int[]a){
        int len=a.length;
        for(int i=0;i<len;i++){//循环次数
            int value=a[i];
            int position=i;
            for(int j=i+1;j<len;j++){//找到最小的值和位置
                if(a[j]<value){
                    value=a[j];
                    position=j;
                }
            }
            a[position]=a[i];//进行交换
            a[i]=value;
        }
    }

不稳定：例如{2, 2, 1}

第一次排：{1, 2, 2 },  2的次序变了

 

4、堆排序（对简单选择排序的优化，将序列构建成大顶堆）

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆

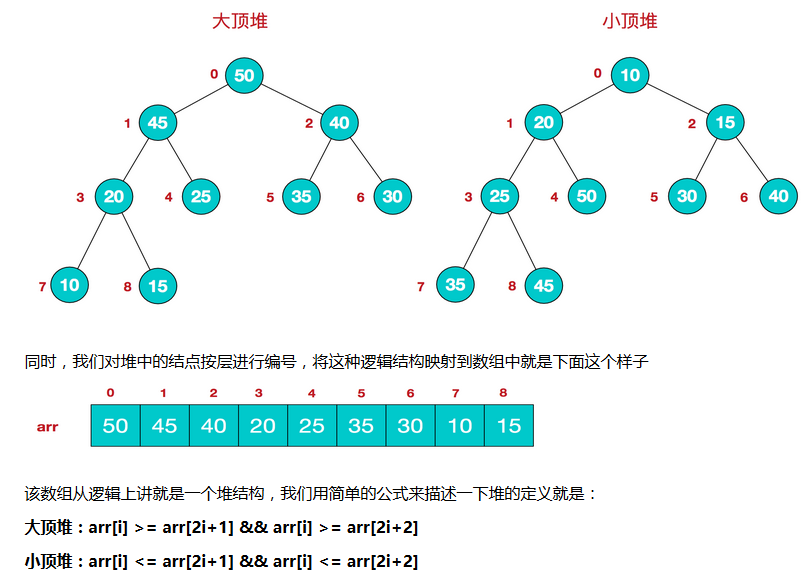
堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。

然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

public  void heapSort(int[] a){
           int len=a.length;
           //循环建堆  
           for(int i=0;i<len-1;i++){
               //建堆  
               buildMaxHeap(a,len-1-i);
               //交换堆顶和最后一个元素  
               swap(a,0,len-1-i);
           }
       }
        //交换方法
       private  void swap(int[] data, int i, int j) {
           int tmp=data[i];
           data[i]=data[j];
           data[j]=tmp;
       }
       //对data数组从0到lastIndex建大顶堆  
       private void buildMaxHeap(int[] data, int lastIndex) {
           //从lastIndex处节点（最后一个节点）的父节点开始  
           for(int i=(lastIndex-1)/2;i>=0;i--){
               //k保存正在判断的节点  
               int k=i;
               //如果当前k节点的子节点存在  
               while(k*2+1<=lastIndex){
                   //k节点的左子节点的索引  
                   int biggerIndex=2*k+1;
                   //如果biggerIndex小于lastIndex，即biggerIndex+1代表的k节点的右子节点存在  
                   if(biggerIndex<lastIndex){
                       //若果右子节点的值较大  
                       if(data[biggerIndex]<data[biggerIndex+1]){
                           //biggerIndex总是记录较大子节点的索引  
                           biggerIndex++;
                       }
                   }
                   //如果k节点的值小于其较大的子节点的值  
                   if(data[k]<data[biggerIndex]){
                       //交换他们  
                       swap(data,k,biggerIndex);
                       //将biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值大于其左右子节点的值  
                       k=biggerIndex;
                   }else{
                       break;
                   }
               }
           }
       }

5、冒泡排序

实现：对相邻的元素进行两两比较，顺序相反则进行交换，这样，每一趟会将最小或最大的元素“浮”到顶端，最终达到完全有序

    public void bubbleSort(int []a){
        int len=a.length;
        for(int i=0;i<len;i++){
            for(int j=0;j<len-i-1;j++){//注意第二重循环的条件
                if(a[j]>a[j+1]){
                    swap(a,j, j+1);
                }
            }
        }
    }
    private void swap(int[] arr, int i, int j){
        int temp=arr[j];
        arr[j]=arr[i];
        arr[i]=temp;
    }

时间复杂度最好时（即是在序列本来就是正序的情况下）是：O(n)

改进版：

    public void bubbleSort(int []a){
        boolean didSwap;
        int len=a.length;
        for(int i=0;i<len;i++){
            didSwap=false;
            for(int j=0;j<len-i-1;j++){//注意第二重循环的条件
                if(a[j]>a[j+1]){
                    swap(a,j, j+1);
                    didSwap=true;
                }
            }
            if(didSwap==false)
                return;
        }
    }
    private void swap(int[] arr, int i, int j){
        int temp=arr[j];
        arr[j]=arr[i];
        arr[i]=temp;
    }

6、快速排序

思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序

（1）以下代码只适合基准数为首位时才可以做到的排序

（如果输入序列是随机的，处理时间是可以接受的。如果数组已经有序时，此时的分割就是一个非常不好的分割。因为每次划分只能使待排序序列减一，此时为最坏情况，快速排序沦为冒泡排序，时间复杂度为）

         public void quickSort(int[] a,int low,int high){
             int start = low;
             int end = high;
             int baseNum = a[low];
             while(end>start){
                 //从后往前比较
                 while(end>start&&a[end]>=baseNum)  //如果没有比关键值小的，比较下一个，直到有比关键值小的交换位置，然后又从前往后比较
                     end--;
                 if(a[end]<=baseNum){
                     int temp = a[end];
                     a[end] = a[start];
                     a[start] = temp;
                 }
                 //从前往后比较
                 while(end>start&&a[start]<=baseNum)//如果没有比关键值大的，比较下一个，直到有比关键值大的交换位置
                    start++;
                 if(a[start]>=baseNum){
                     int temp = a[start];
                     a[start] = a[end];
                     a[end] = temp;
                 }
             //此时第一次循环比较结束，关键值的位置已经确定了。左边的值都比关键值小，右边的值都比关键值大，但是两边的顺序还有可能是不一样的，进行下面的递归调用
             }
             //递归
             if(start>low) quickSort(a,low,start-1);//左边序列。第一个索引位置到关键值索引-1
             if(end<high) quickSort(a,end+1,high);//右边序列。从关键值索引+1到最后一个
         }

（2）三数取中法：使用左端、右端和中心位置上的三个元素的中值作为基准元

使用三数中值分割法消除了预排序输入的不好情形，并且减少快排大约5%的比较次数

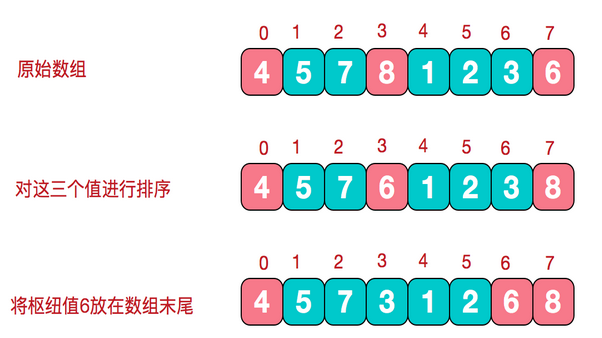
 根据枢纽值进行分割

 

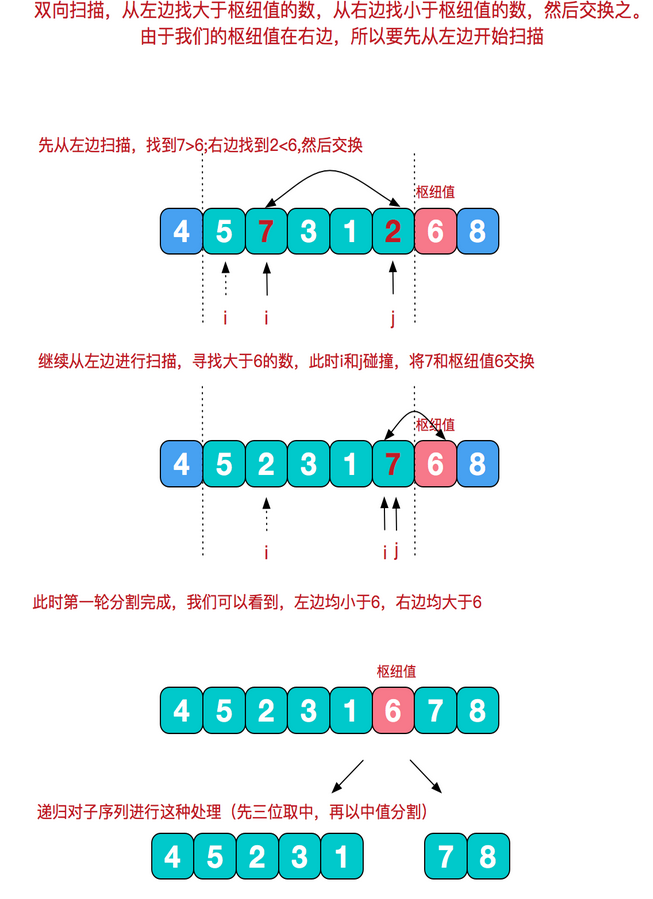
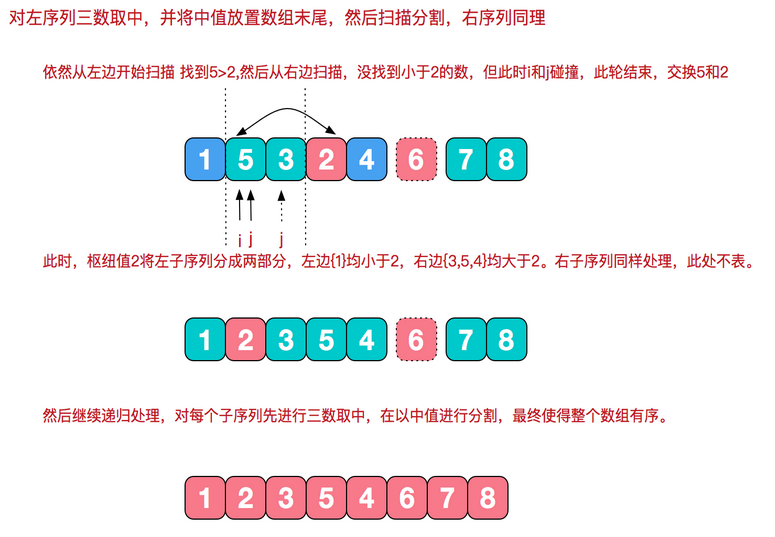
private static int[] quickSort(int[] array, int low, int high) {
        dealPivot(array, low, high);
        int start = low;
        int end = high-1;
        int baseNum = array[high - 1];
        while (start < end) {
            while (end > start && baseNum >= array[start]) {
                start++;
            }
            if (baseNum<=array[start]) {
                swap(array,start,end);
            }
            while (end > start && baseNum <= array[end]) {
                end--;
            }
            if (baseNum>=array[end]) {
                swap(array,start,end);
            }
        }
        if (start > low)
            quickSort(array, low, start - 1);    
        return array;
    }
    
    private static void dealPivot(int[] array, int left, int right) {
        int mid = (left + right) / 2;
        if (array[left] > array[mid])
            swap(array, left, mid);
        if (array[left] > array[right])
            swap(array, left, right);
        if (array[mid] > array[right])
            swap(array, mid, right);
        swap(array, right - 1, mid);
    }

    private static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

时间复杂度分析：

最好：每次主元将数组划分为规模大致相等的两部分。设 T(n) 表示使用快速排序算法对包含 n 个元素的数组排序所需的时间，因此，和归并排序的分析相似，快速排序的 T(n)= O(nlogn)

最坏：划分由 n 个元素构成的数组需要进行 n 次比较和 n 次移动。因此划分所需时间为 O(n) 。最差情况下，每次主元会将数组划分为一个大的子数组和一个空数组。这个大的子数组的规模是在上次划分的子数组的规模减 1 。该算法需要 (n-1)+(n-2)+…+2+1= O(n2) 时间

不稳定举例：

例如：{ 2(a) , 2(b), 1}

以第一个2为基准数

{1， 2(b) ， 2(a)}

2的次序变了

7、归并排序（采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之）

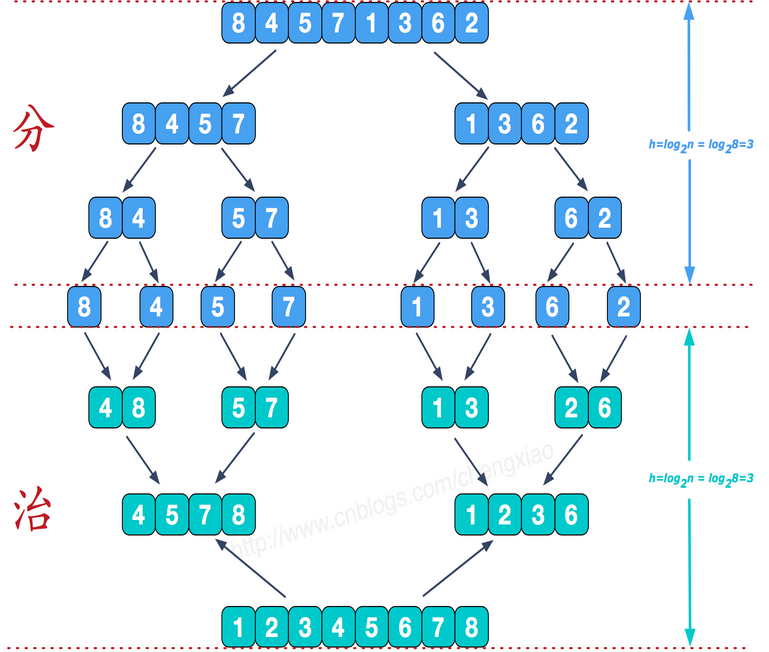
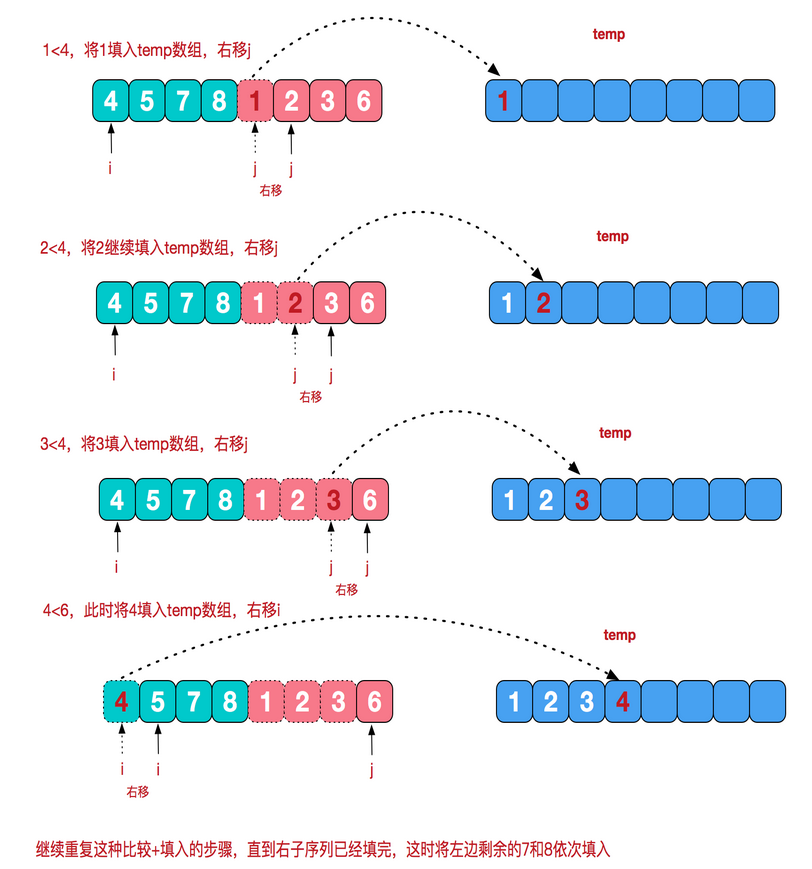
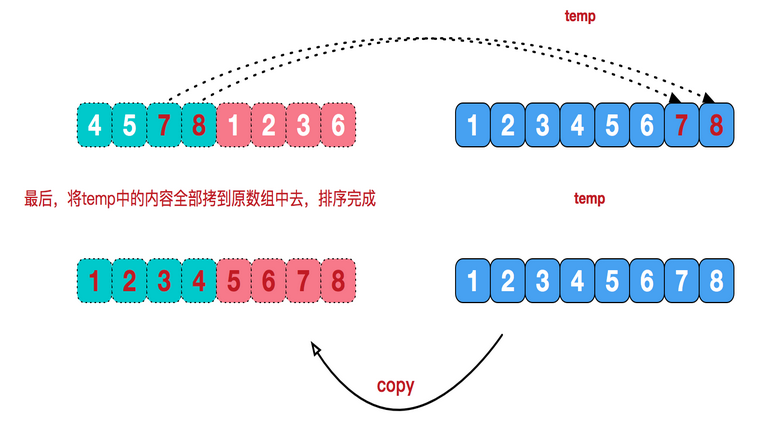
public static void mergeSort(int [] a){
            int []temp = new int[a.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
            sort(a,0,a.length-1,temp);
        }
        private static void sort(int[] arr,int left,int right,int []temp){
            if(left<right){
                int mid = (left+right)/2;
                sort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
                sort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
                merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
            }
        }
        private static void merge(int[] arr,int left,int mid,int right,int[] temp){
            int i = left;//左序列指针
            int j = mid+1;//右序列指针
            int t = 0;//临时数组指针
            while (i<=mid && j<=right){
                if(arr[i]<=arr[j]){
                    temp[t++] = arr[i++];
                }else {
                    temp[t++] = arr[j++];
                }
            }
            while(i<=mid){//将左边剩余元素填充进temp中
                temp[t++] = arr[i++];
            }
            while(j<=right){//将右序列剩余元素填充进temp中
                temp[t++] = arr[j++];
            }
            t = 0;
            //将temp中的元素全部拷贝到原数组中
            while(left <= right){
                arr[left++] = temp[t++];
            }
        }