题目大意
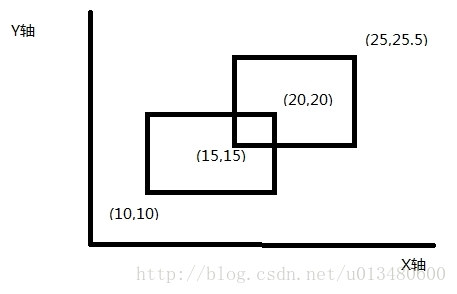
给你n个矩形,让你求所有矩形覆盖的总面积,重叠的地方只算一次
输入格式
输入的第一行包含一个整数n,表示可得到的地图数目。
以下n行,每行描述一张地图。每行包含4个整数x1,y1,x2和y2(0≤x1<x2≤30000,0≤y1<y2≤30000)。数值(x1,y1)和(x2,y2)是坐标,分别表示绘制区域的左下角和右上角坐标。每张地图是矩形的,并且它的边是平行于x坐标轴或y坐标轴的。
数据可能有多组,当n为零时停止输入
输出格式
对于每个测试数据,你的程序应该输出一个答案。每个答案的第一行必须是“Test case #k”,其中k是测试数据的编号(从1开始)。第二个必须是“Total explored area: a”,其中a是总探索面积(即在本测试案例中所有矩形的并集面积),精确到小数点右边两位。
在每个测试用例后输出一个空行。
样例输入
2
10 10 20 20
15 15 25 25.5
0
样例输出
Test case #1
Total explored area: 180.00
数据范围
n <= 100
主要思路:线段树 + 扫描线
这是一道扫描线裸题。
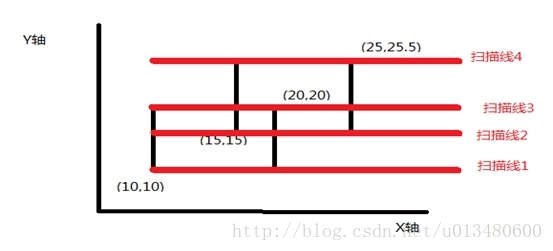
我们把要覆盖的矩形抽象成两个线,这两条线就被称为扫描线。如图(网上扒拉来的图QwQ,若有侵权请联系博主删除QwQ)
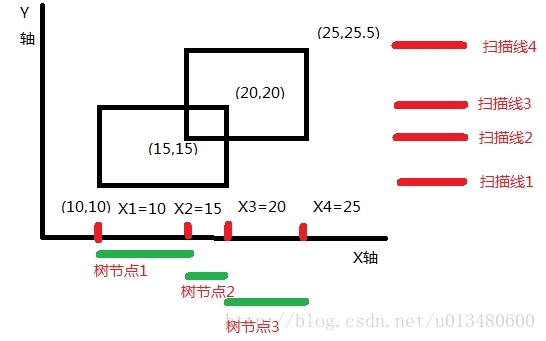
对于扫描线,我们可以把扫描线的高度进行离散化。然后我们把x轴上的线(图中的黑线)分隔开的就可以抽象成几段线段。
我们只需要把这些交点用线段树维护就好。然后我们把所有扫描线从最小到最大排序一下。我们首先记录一条扫描线的左端点与右端点,它的高度,它是下底边还是上界边,如果是下底边就记为1,上界边记为-1。(这里实际是做了个差分,就是维护两条扫描线穿过(或切于边界的)矩形有多少。
线段树中维护的是这段区间的下底边个数和下底边总长度。我们扫描的作是每次更新下底边总长度和下底边个数增加新面积。我们只要从最下向上扫描一遍统计总面积就好了。
code:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <ctime>
#include <algorithm>
#include <queue>
#include <stack>
#include <map>
#include <vector>
using namespace std;
#define go(i, j, n, k) for(int i = j; i <= n; i += k)
#define fo(i, j, n, k) for(int i = j; i >= n; i -= k)
#define inf 1 << 30
#define mn 100010
#define ll long long
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch > '9' || ch < '0') { if(ch == '-') f = -f; ch = getchar(); }
while(ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
return x * f;
}
struct tree{
int mark; double sum;
} z[mn << 2];
struct seg{
double l, r, h;
int d;
seg() {}
seg(double _l, double _r, double _h, int _d) : l(_l), r(_r), h(_h), d(_d) {}
bool operator < (const seg &b) const { return h < b.h; }
} s[mn];
int n, num, kkk;
double ha[mn];
double x, y, xx, yy;
#define root 0, m - 1, 1
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define bson l, r, rt
inline void update(int l, int r, int rt) {
if(z[rt].mark) z[rt].sum = ha[r + 1] - ha[l];
else if(l == r) z[rt].sum = 0;
else z[rt].sum = z[rt << 1].sum + z[rt << 1 | 1].sum;
}
inline void modify(int l, int r, int rt, int nowl, int nowr, int d) {
if(nowl <= l && r <= nowr) {
z[rt].mark += d;
update(bson);
return;
}
int m = (l + r) >> 1;
if(nowl <= m) modify(lson, nowl, nowr, d);
if(m < nowr) modify(rson, nowl, nowr, d);
update(bson);
}
inline int search(double key, double* x, int n) {
int l = 0, r = n - 1;
while(l <= r) {
int m = (l + r) >> 1;
if(x[m] == key) return m;
if(x[m] > key) r = m - 1;
else l = m + 1;
}
return -1;
}
int main() {
while(cin >> n, n) {
num = 0;
go(i, 0, n - 1, 1) {
cin >> x >> y >> xx >> yy;
ha[num] = x;
s[num++] = seg(x, xx, y, 1);
ha[num] = xx;
s[num++] = seg(x, xx, yy, -1);
}
sort(ha, ha + num);
sort(s, s + num);
int m = 1;
go(i, 1, num - 1, 1)
if(ha[i] != ha[i - 1]) ha[m++] = ha[i];
double ans = 0;
go(i, 0, num - 1, 1) {
int L = search(s[i].l, ha, m);
int R = search(s[i].r, ha, m) - 1;
modify(root, L, R, s[i].d);
ans += z[1].sum * (s[i + 1].h - s[i].h);
}
printf("Test case #%d
Total explored area: %.2lf
", ++kkk, ans);
}
return 0;
}