算法练习之矩形的交集与并集的计算

这是一道竞赛的题目，如下：

在编写图形界面软件的时候，经常会遇到处理两个矩形的关系。

如图【1.jpg】所示，矩形的交集指的是：两个矩形重叠区的矩形，当然也可能不存在（参看【2.jpg】）。两个矩形的并集指的是：能包含这两个矩形的最小矩形，它一定是存在的。

           

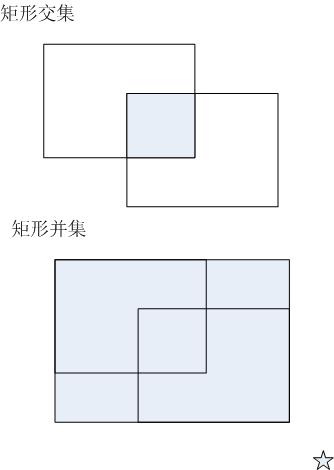
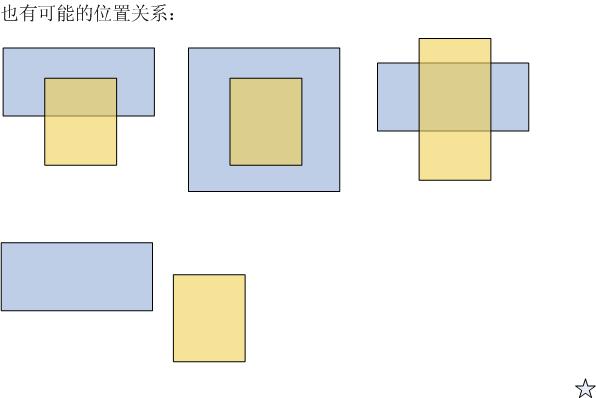
本题目的要求就是：由用户输入两个矩形的坐标，程序输出它们的交集和并集矩形。

矩形坐标的输入格式是输入两个对角点坐标，注意，不保证是哪个对角，也不保证顺序（你可以体会一下，在桌面上拖动鼠标拉矩形，4个方向都可以的）。

输入数据格式：
x1,y1,x2,y2
x1,y1,x2,y2

数据共两行，每行表示一个矩形。每行是两个点的坐标。x坐标在左，y坐标在右。坐标系统是：屏幕左上角为(0,0)，x坐标水平向右增大；y坐标垂直向下增大。

要求程序输出格式：
x1,y1,长度,高度
x1,y1,长度,高度

也是两行数据，分别表示交集和并集。如果交集不存在，则输出“不存在”

前边两项是左上角的坐标。后边是矩形的长度和高度。

例如，用户输入：
100,220,300,100
150,150,300,300

则程序输出：
150,150,150,70
100,100,200,200

例如，用户输入：
10,10,20,20
30,30,40,40

则程序输出：
不存在
10,10,30,30

题目给人的第一感觉并不是很难，但可能繁琐~~

我的第一种想法就是先求“并集矩形”因为这个会很好求，那用什么数据结构来表示呢？

显然，保存矩形的四个顶点咯，用一个Point类来保存：

class Point {
    int x;
    int y;
}

但，仔细想一想，实际上我们并不需要太多的数据！

 我们要确定一个矩形，只需要矩形的起始x坐标、结束x坐标、起始y坐标和结束y坐标。文字不好说，看图吧：

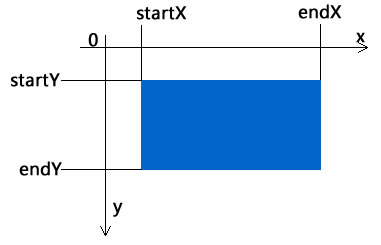
 所以，保存一个矩形类我们可以这样写：

class Rect {
    public int startX;
    public int endX;
    public int startY;
    public int endY;
}

题目中，x1,y1和x2,y2这两个点并不一定是从左上角到右下角这两个点，但一定是对角线上的！所以根据大小关系还是很好确定的：

public Rect(String str) {
    String[] l = str.split(",");
    int x1 = Integer.parseInt(l[0]);
    int y1 = Integer.parseInt(l[1]);
    int x2 = Integer.parseInt(l[2]);
    int y2 = Integer.parseInt(l[3]);
    startX = x1 < x2 ? x1 : x2;
    endX = x1 > x2 ? x1 : x2;
    startY = y1 < y2 ? y1 : y2;
    endY = y1 > y2 ? y1 : y2;
}

一个可以从字符串直接生成矩形的构造方法~~~。

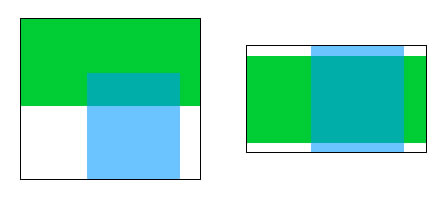
从上图不难看出，“并集矩形”的startX是由矩形1和矩形2的startX中比较小的那个来决定的，endX由比较大的endX决定。所以，“并集矩形”的求法就很简单了：

// 由两个矩形构造出他们的“并集矩形”
public Rect(Rect r1, Rect r2) {
    startX = r1.startX < r2.startX ? r1.startX : r2.startX;
    endX = r1.endX > r2.endX ? r1.endX : r2.endX;
    startY = r1.startY < r2.startY ? r1.startY : r2.startY;
    endY = r1.endY > r2.endY ? r1.endY : r2.endY;
}

“交集矩形”貌似就麻烦多了，有几种情况要进行判断。

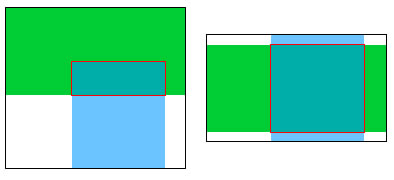
观察图中的红色框，可以得到一个简单的结论：“交集矩形”的startX由较大的startX决定、endX由较小的endX决定，Y也是同样的情况。

但是，对于没有交集的情况呢？

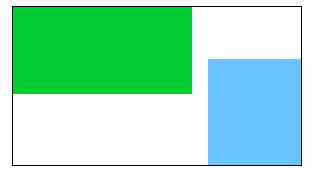
我们用上面的方法进行推导，“交集矩形”的startX就是蓝色矩形的startX，endX就是绿色矩形的endX。显然，startX大于endX。这样的矩形应该是不存在的。对于Y轴应该也是同样的情况。

找到了规律求解也就不难了，所有代码如下：

public class Test {
    public static void main(String[] args) {
        Rect r1 = new Rect("100,220,300,100");
        Rect r2 = new Rect("150,150,300,300");
        Rect merge = new Rect(r1, r2);
        Rect both = Rect.getBothArea(r1, r2);
        both.printInfo();
        merge.printInfo();
        System.out.println("~~~~~~~~~~~~~~~~~~~~~~");
        r1 = new Rect("10,10,20,20");
        r2 = new Rect("30,30,40,40");
        merge = new Rect(r1, r2);
        both = Rect.getBothArea(r1, r2);
        both.printInfo();
        merge.printInfo();
    }
}

class Rect {
    public int startX;
    public int endX;
    public int startY;
    public int endY;

    public Rect() {
    }

    // 由两个矩形构造出他们的“并集矩形”
    public Rect(Rect r1, Rect r2) {
        startX = r1.startX < r2.startX ? r1.startX : r2.startX;
        endX = r1.endX > r2.endX ? r1.endX : r2.endX;
        startY = r1.startY < r2.startY ? r1.startY : r2.startY;
        endY = r1.endY > r2.endY ? r1.endY : r2.endY;
    }

    public static Rect getBothArea(Rect r1, Rect r2) {
        Rect merge = new Rect(r1, r2);
        Rect both = new Rect();
        both.startX = r1.startX == merge.startX ? r2.startX : r1.startX;
        both.endX = r1.endX == merge.endX ? r2.endX : r1.endX;
        both.startY = r1.startY == merge.startY ? r2.startY : r1.startY;
        both.endY = r1.endY == merge.endY ? r2.endY : r1.endY;
        return both;
    }

    public Rect(String str) {
        String[] l = str.split(",");
        int x1 = Integer.parseInt(l[0]);
        int y1 = Integer.parseInt(l[1]);
        int x2 = Integer.parseInt(l[2]);
        int y2 = Integer.parseInt(l[3]);
        startX = x1 < x2 ? x1 : x2;
        endX = x1 > x2 ? x1 : x2;
        startY = y1 < y2 ? y1 : y2;
        endY = y1 > y2 ? y1 : y2;
    }

    public void printInfo() {
        if (startX >= endX || startY >= endY) {
            System.out.println("不存在");
        } else {
            System.out.println(startX + "," + startY + "," + (endX - startX) + ","
                    + (endY - startY));
        }
    }
}

代码比想象中的少得多了~~~

后记：一开始先分析题目，找出解题的突破口比一上来就蛮干要强得多！记得自己第一次做这题就是没仔细思考，用四个Point来保存矩形，最后，关系太多，把自己给绕晕了~~~

yjiyjige 2013.4.20