【软工】个人项目作业

项目	内容
作业所属的课程	2020春季计算机学院软件工程(罗杰 任健)
作业的要求	个人项目作业
我在这门课程的目标是	学会使用软件工程的设计思想和方法，能够设计出高效并且可用性、可维护性、可拓展性较高的软件。
这个作业在哪些方面帮助我实现目标	初步学习效能分析以及个人软件开发流程，实际练习应用并熟悉相关的工具链。
参考资料	《构建之法：现代软件工程（邹欣 著）》
我所属的教学班级	005
可克隆的GitHub地址	https://github.com/Jiyuan-Yang/SE_PSP_Project_17373187.git

PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	240	300
· Design Spec	· 生成设计文档	30	45
· Design Review	· 设计复审 (和同事审核设计文档)	10	10
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	10
· Design	· 具体设计	30	20
· Coding	· 具体编码	180	200
· Code Review	· 代码复审	20	30
· Test	· 测试（自我测试，修改代码，提交修改）	40	60
Reporting	报告
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	30	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	40	40
	合计	670	785

这次花费时间最长的部分在于需求分析（包括学习新技术）以及具体编码。其原因在于，具体进行需求分析时，考虑到对性能的要求，希望能够找到一个更加高效的方法，尝试去查找了一些资料但是很多判定的方法都有一些局限性，不太适合这次的问题，因此最终花费了一些时间还是选择直接求解。同时由于之前使用C编程比较多，对C++的了解比较少，所以这次在开始之前，着重对C++的面向对象以及相关的关联性容器进行了学习，花费了更多的时间。同样，在具体编码时，由于不熟悉C++的使用，对于类的编写以及命名空间的理解使用上也花了一些时间。

解题思路描述

首先，拿到题目后，从大体的设计角度来讲，可以将直线和圆作为两个图形类，同时由于需要求交点，所以另外还需要有一个点类。之后，对于点类，由于想要使用set容器进行去重，因此需要重写小于的运算符。对于直线类和圆类，应该实现求交点的方法。

接下来对于求交点的具体实现，进行资料查找。交点分为三种：直线与直线、直线与圆、圆与圆之间的交点。

• 直线与直线

  • 表示形式：直线使用一般式进行表示，记为ax + by + c = 0。

  • 求解一般式

    设直线上的两点P1(x1, y1) P2(x2, y2)，则有

    a = y2 - y1

    b = x1 - x2

    c = x2 * y1 - x1 * y2

  • 求交点

    设一般式为a0x + b0y + c0 = 0和a1x + b1y + c1 = 0，则两直线的交点为：

    D = a0 * b1 - a1 * b0

    若D = 0则两直线平行或重合（在本题设下只会为平行），否则有交点：

    x = (b0 * c1 - b1 * c0) / D

    y = (c0 * a1 - c1 * a0) / D

• 直线与圆

  • 圆的表示形式：使用圆心和半径进行表示。

  • 求交点

    先求圆心在直线上的投影点(Xpr, Ypr)

    用投影点坐标和圆心坐标求圆心到直线的距离d

    若d > r则直线与圆无交点，d = r则有唯一交点，d < r则有两个不同的交点

    使用勾股定理求出半弦长，然后由直线的方向单位向量可以与半弦长相乘可以求出两个方向的向量，分别与圆心在直线上的投影点求和，即可得到两个交点的坐标（如果相切，则两坐标相同）

• 圆与圆

  • 求交点

    求圆心之间的距离d，设两个圆的半径分别为r1和r2，若0 <= d < |r1 - r2|，或d > r1 + r2，则没有交点。若 d = |r1 - r2|，或d = r1 + r2，则有唯一交点。若|r1 - r2| < d < r1 + r2，则有两个不同的交点。

    当存在交点时，在两圆心以及一个交点组成的三角形中，使用余弦定理，可以求出圆心和交点的连线与圆心和另一个圆的圆心之间的连线的夹角a，同时可以求出该从圆心指向另一个圆圆心的向量与x轴正方向夹角t，因此可以知道该圆心与两个交点（可相同，相同时a = 0）的连线与x轴正方向夹角为t + a与t - a，由此，根据圆心坐标即可求解交点坐标

设计实现过程

程序设计

根据以上的分析，一共划分了3个类，分别是Point、Line、Circle。

• Point类
  • 成员变量：x，y，可见性为private。分别表示点的横纵坐标。
  • get方法，用于获取x，y变量。
  • 重写<运算符。
• Line类
  • 成员变量：x0，y0，x1，y1，可见性为private，表示直线经过的点，以及直线一般式中的参数a，b，c。
  • get方法。
  • getLineIntersectPoint。静态函数，用于求两直线的交点，并将其加入传入的集合。
• Circle类
  • 成员变量：x，y，r，可见性为private，表示圆的圆心坐标以及半径。
  • get方法。
  • getLineCircleIntersect。静态函数，用于求直线与圆的交点，并将其加入传入的集合。
  • getCircleIntersect。静态函数，用于求圆与圆的交点，并将其加入传入的集合。

最后，在main函数中，对输入参数进行解析，然后读取输入数据，将直线和圆分别进行保存。每次新增一个图形，就与其他的图形求交点。将所有交点保存在一个set里进行去重，最后输出set的大小。

单元测试设计

• Point类
  • 这一类中最主要的部分就是对<运算符的重写，也是重点测试对象。首先先进行一般样例的测试，创建一些点，同时里面有重复的点，加入到set中，判断能否将重复点合并。同时又考虑到由于double的精度比较高，所以比较两个double类型的浮点数时不能使用直接相等，而是做差，以差值的大小进行判定。
  • 此外，为了保证覆盖率，对get方法也进行简单的测试。
• Line类
  • 一方面是对构造方法与get方法的测试，主要判断能否正确计算出一般式。
  • 另一方面是测试直线之间的交点。分别对平行的情况以及相交的情况进行测试。
• Circle类
  • 对get方法的简单测试。
  • 测试直线与圆的交点，要测试直线与圆相离、相切、相交。
  • 测试圆与圆的交点，要测试圆与圆内含、内切、相交、外切、相离。

程序性能分析

首先是总体的性能分析，从下面的图中可以看到，其中很大一部分时间都是被std::Tree_中的操作所消耗的。后来经过查找，在C++中，set的构建是基于红黑树的构建的，这也是要对自定义的类使用set方法时需要重写小于运算符的原因。因此，程序的时间消耗很大一部分是在向set中添加元素导致的。

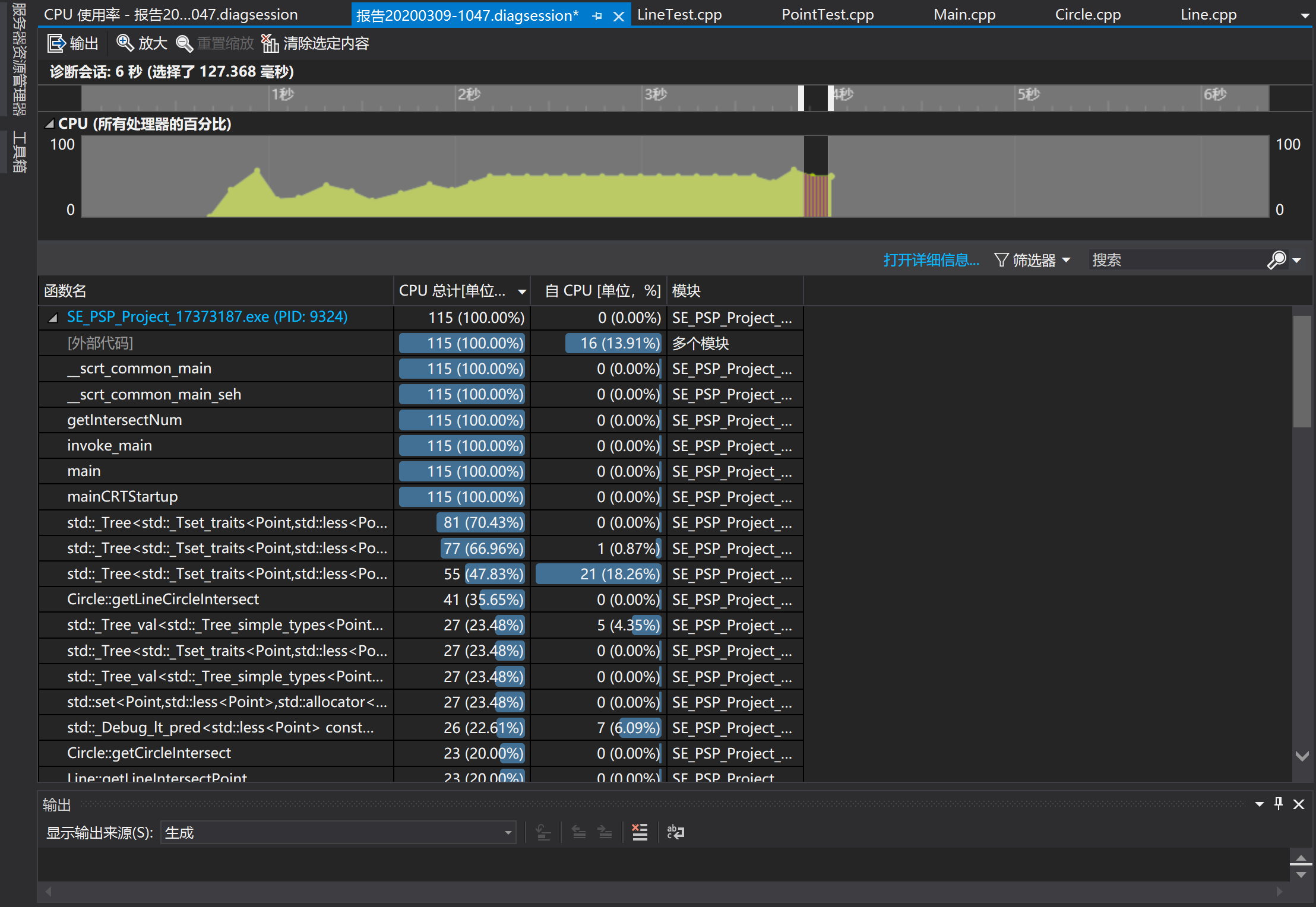
在进一步查看自己写的三个求交点的主要函数中的性能消耗时，进一步证实了这一点，很大一部分都消耗在了调用一个set的insert方法时。

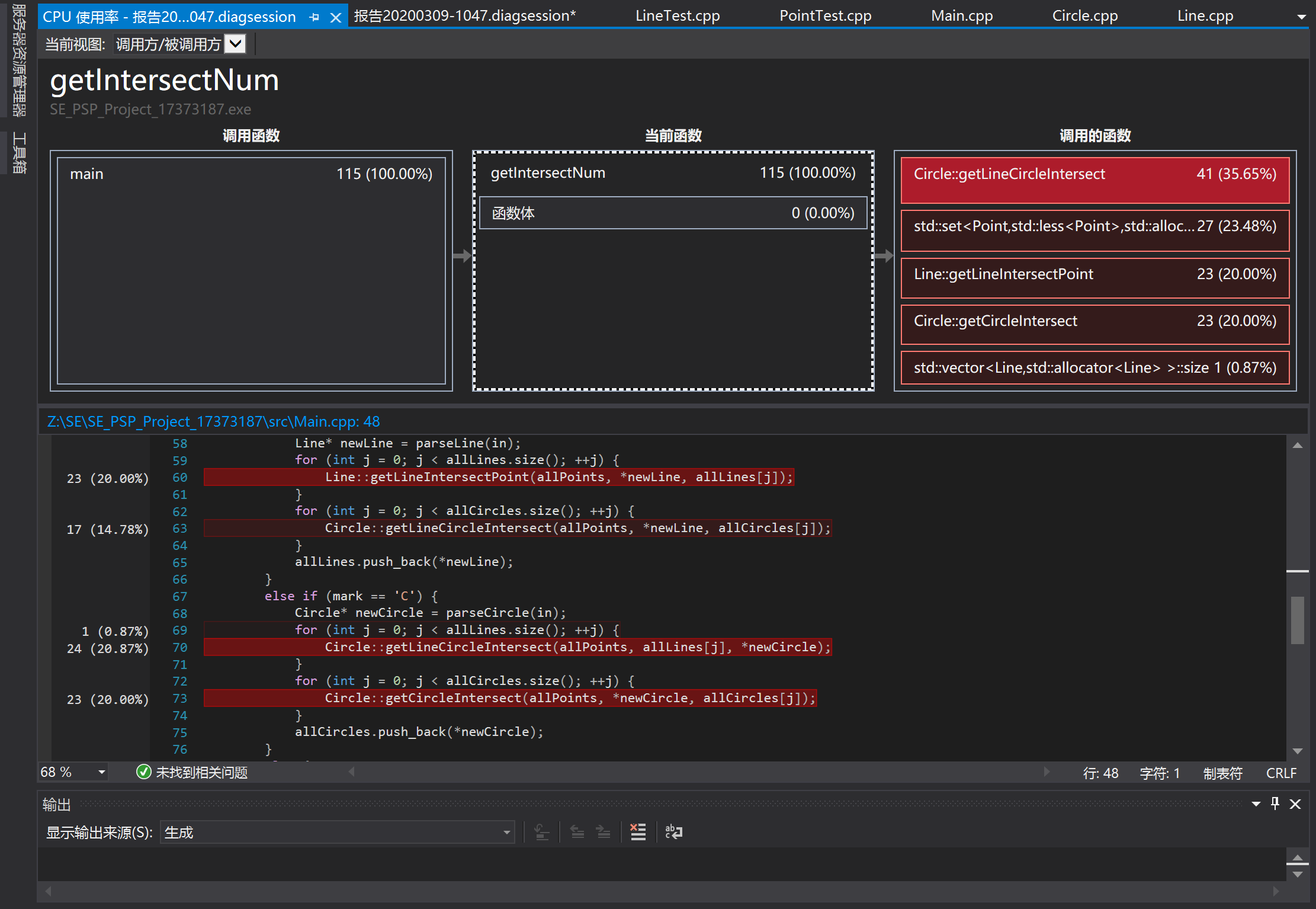
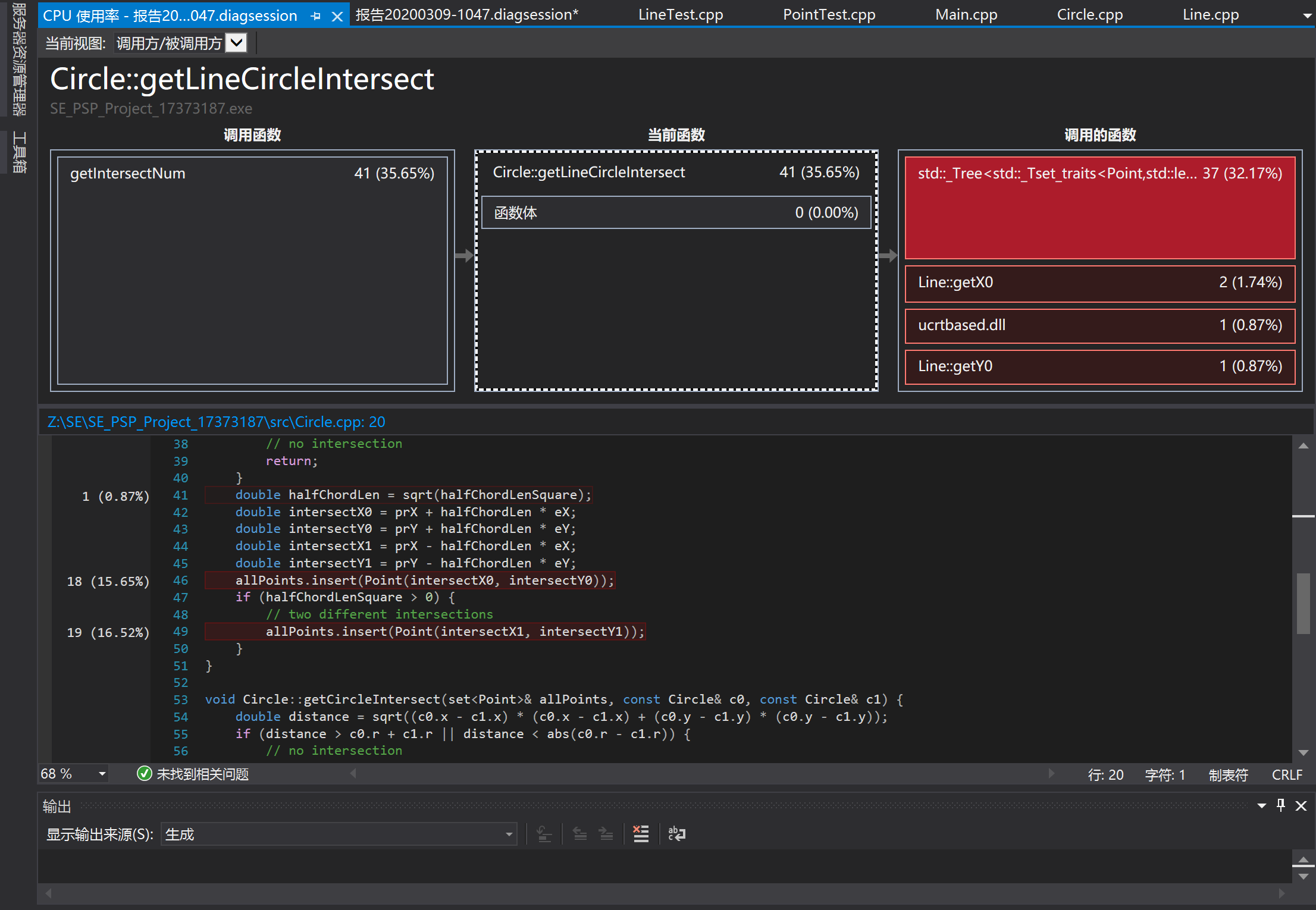
因此去查找是否有比set更加高效的关联性容器，在这篇博客中，找到了“无序容器”，对于set，具体而言是使用unordered_set。使用unordered_set的一个关键是构造合适的哈希函数，尽可能减少哈希冲突，在一篇博客中找到了下面的写法：

inline size_t operator()(const pair<int,int> & p) const {
    return p.first * 100 + p.second;
}

在这篇博客的题设中，点的坐标都是1到100的整数，因此想法是将横坐标映射到高三位，纵坐标映射到低三位，使用二者求和避免冲突。但是在我们的题设中点的范围是(-100000, 100000)，同时在计算中经常会出现非整数的情况，又因为unordered_set使用哈希函数判别是否是同一个元素，所以在这里一旦造成哈希冲突，则可能导致漏点的情况。因为没有想出一个合理的哈希函数的设计，因此这个想法只能作罢。

代码说明

这里主要就求直线与直线、直线与圆、圆与圆的交点的方法进行说明。

• 直线与直线的交点

  直接根据“解题思路描述”部分的方法计算即可。

  double d = l0.a * l1.b - l1.a * l0.b;
  if (d == 0) {
  	// two lines has no intersecting point
  	return;
  }
  else {
  	double x = (l0.b * l1.c - l1.b * l0.c) / d;
  	double y = (l1.a * l0.c - l0.a * l1.c) / d;
  	allPoints.insert(Point(x, y));
  }
  

• 直线与圆的交点

  double lineVectorX = (double) l.getX1() - l.getX0();
  double lineVectorY = (double) l.getY1() - l.getY0();
  double lineCircleVectorX = c.x - l.getX0();
  double lineCircleVectorY = c.y - l.getY0();
  double dot = (lineVectorX * lineCircleVectorX + lineVectorY * lineCircleVectorY);
  double modSquare = (lineVectorX * lineVectorX + lineVectorY * lineVectorY);
  double ratio = dot / modSquare;
  
  double prX = l.getX0() + ratio * lineVectorX;
  double prY = l.getY0() + ratio * lineVectorY;
  

  以上用于求解圆心在直线上的投影点。lineVector即由确定直线的两点确定的向量。lineCircleVector是从(x0, y0)点指向圆心的向量。二者做点乘并除以由确定直线的两点确定的向量的模的平方得到的即(x0, y0)到投影点与(x0, y0)到(x1, y1)的长度之比。由此，并结合(x0, y0)即可计算投影点的坐标。

  double eX = lineVectorX / sqrt(modSquare);
  double eY = lineVectorY / sqrt(modSquare);
  

  计算直线的单位方向向量。

  double halfChordLenSquare = c.r * c.r - ((prX - c.x) * (prX - c.x) + (prY - c.y) * (prY - c.y));
  if (halfChordLenSquare < 0) {
  	// no intersection
  	return;
  }
  double halfChordLen = sqrt(halfChordLenSquare);
  

  由勾股定理计算半弦长，之后使用投影点的坐标与半弦长乘以单位方向向量进行加和减即可得到两交点坐标。

• 圆与圆的交点

  具体思路同见“解题思路描述”部分，代码中的a与t与之前描述中的a与t。

  double distance = sqrt((c0.x - c1.x) * (c0.x - c1.x) + (c0.y - c1.y) * (c0.y - c1.y));
  if (distance > c0.r + c1.r || distance < abs(c0.r - c1.r)) {
  	// no intersection
  	return;
  }
  // use Law of cosines to get the angle `a` between distance vector and radium vector
  double a = acos((c0.r * c0.r + distance * distance - c1.r * c1.r) / (2 * c0.r * distance));
  // get the angle `t` between distance vector and x-axis
  double t = atan2(c1.y - c0.y, c1.x - c0.x);
  double intersectX0 = c0.x + c0.r * cos(t + a);
  double intersectY0 = c0.y + c0.r * sin(t + a);
  double intersectX1 = c0.x + c0.r * cos(t - a);
  double intersectY1 = c0.y + c0.r * sin(t - a);
  allPoints.insert(Point(intersectX0, intersectY0));
  if (distance > abs(c0.r - c1.r) && distance < c0.r + c1.r) {
  	// 2 interactions
  	allPoints.insert(Point(intersectX1, intersectY1));
  }
  

消除所有警告截图