求树的直径两种方法/树形dp学习

失踪了几个月 我再次回来学习算法了。感觉有点来不及了QAQ

 

希望自己继续努力吧 加油少年！相信自己 拥有无限可能！！！

两种方法求树的直径

何为树的直径？直径既是数值概念，又指的是路径，一般初学我们要学习的是求如何求直径的长度

怎么样去求一棵树的直径呢？

1. 任取一个点作为起点，找到距离该点距离最大的一个点u
2. 再找到距离u最远的点v
3. 则u与v间的路径就是一条直径

为什么这个做法是正确的呢？

事实上 我们只要证明u一定是某条直径的一个端点，那么很显然就可以说明u与v之间的路径是一条直径

证明过程

假设已知BC为直径（当然画的不太像原谅我

u是距离A最远的点

情况一：直径与au不相交（注在这份图中D点就是u

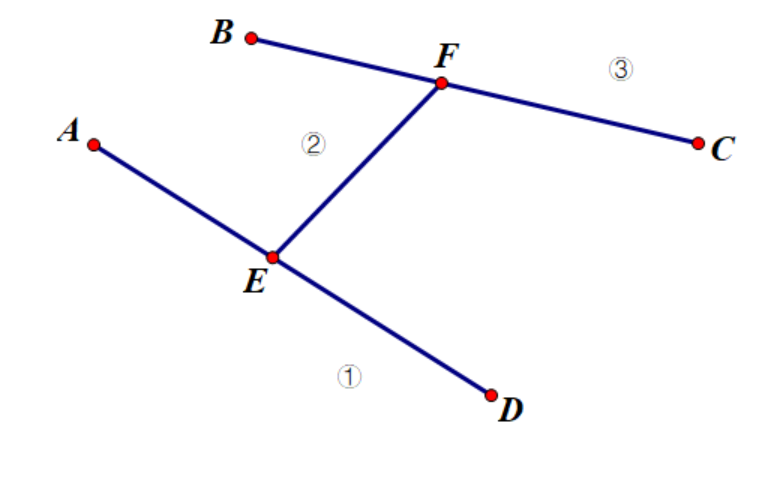
 显然 ① ≥ ② + ③；

所以 ① + ② ≥③

此时u即为直径的端点

情况二：直径与au相交

 

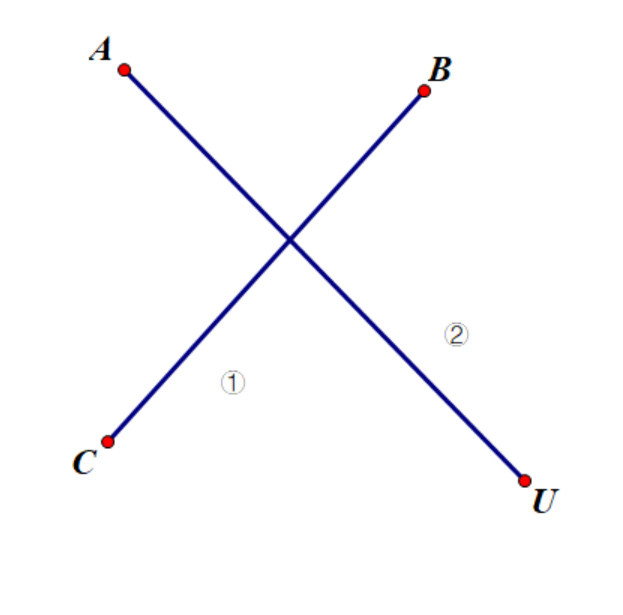
由定义可知 ②≥① 显然u也是直径的端点

综上，uv一定是直径得证。

对于树的直径 有两种做法 一种是搜索（深搜广搜其实更推荐bfs）还有就是dp

两次dfs求直径

dfs就是按照上面的做法直接做就好了

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010, M = N * 2, INF = 0x3f3f3f3f;

int n,m;
int h[N], e[M], w[M], ne[M], idx,ans;
int d[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u, int father)
{
    if(d[u] > ans)
    {
        ans = d[u];
        m = u;    
    }
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        d[j] = d[u] + w[i];
        dfs(j,u);
    }
    return ;
}

int main()
{
    cin >> n;
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c), add(b, a, c);
    }

    dfs(1,-1);
    ans = 0;
    d[m] = 0;
    dfs(m,-1);

    printf("%d
", ans);

    return 0;
}

树形dp求直径

把所有直径（路径概念）都算一下，找个最大值

直径直接枚举太复杂，不如枚举点，看作是一个点把直径提起来，那么我只要算两边的长度就好了。

找到一个最大路径和次大路径 所构成的就是最长路径

#include <iostream>
#include <cstring>
#include <algorithm>


using namespace std;

const int N = 100010;
const int M = N << 1;

int h[N],ne[M],e[M],w[M],idx,ans;

int n;

inline void add(int a,int b,int c)
{
    e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx ++;
}


int dfs(int u,int father)
{
    int d1 = 0,d2 = 0;
    for(int i = h[u];i != -1;i = ne[i])
    {
        int j = e[i];
        if(j == father) continue;
        int dist = dfs(j,u) + w[i];
        if(dist > d1)
        {
            d2 = d1,d1 = dist;
        }
        else if(dist > d2)
        {
            d2 = dist;
        }
    }
    
    ans = max(ans,d1 + d2);
    return d1;
}

signed main()
{
    memset(h,-1,sizeof h);
    cin >> n;
    for(int i = 1; i < n; ++ i)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
        add(b,a,c);
    }
    
    dfs(1,-1);
    cout << ans << endl;
    return 0;
}