一 概述
- 回归分析模型:销售额 =93765+0.3* 百度+0.15 * 社交媒体+0.05 *电话直销+0.02 * 短信
- 线性回归
- 研究自变量 x 对因变量 y 影响的一种数据分析方法
- 可以表示为Y=ax+b+ε,其中Y为因变量,x为自变量,a为影响系数,b为截距,ε为随机误差。
- 常见应用场景
- 主要应用场景是进行预测和控制例如计划制定、KPI制定、目标制定等
- 也可以基于预测的数据与实际数据进行比对和分析,确定事件发展程度并给未来行动提供方向性指导
二 案例演示
目的:计算各个宣传渠道对销售额的影响
1 预处理过的数据
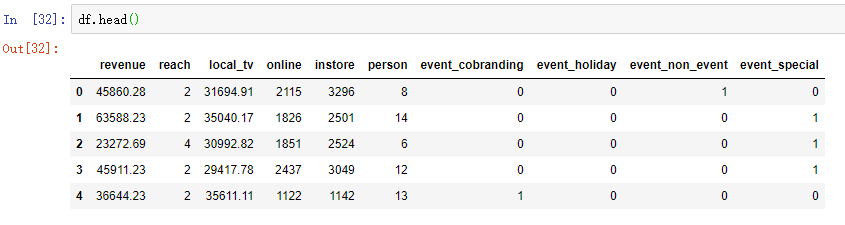
2 相关性分析
df.corr()[['revenue']].sort_values(by='revenue', ascending=False)
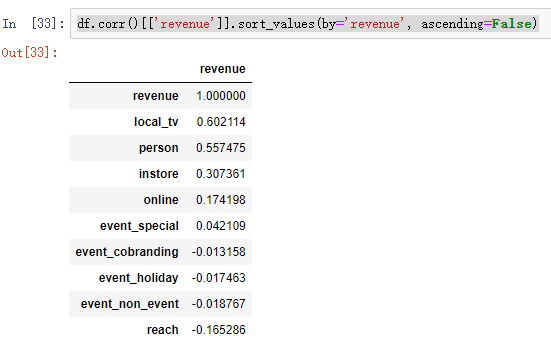
3 线性回归分析 建模
注意:数据有缺失会报错
1> 建模核心代码
from sklearn.linear_model import LinearRegression line_model = LinearRegression() # 设定因变量 y = df['revenue'] # 设定自变量 x = df[['local_tv','person','instore']] a = line_model.fit(x,y)
2> 指标
自变量系数
line_model.coef_
截距
line_model.intercept_
4 模型评估
模型得分:score 越高越好
score = line_model.score(x,y)
利用特征去计算(预测)y 的预测值
prediction = line_model.predict(x)
计算误差
error = prediction - y
均方根误差 rmse 越小越好【后附公式】
rmse = (error**2).mean()**0.5
计算平均绝对误差 mae 越小越好【后附公式】
mae = abs(error).mean()
附:
1> 直接用 sklearn 中的方法计算 rmse 和 mae
import numpy as np from sklearn.metrics import mean_squared_error, mean_absolute_error # 根均方误差(RMSE) np.sqrt(mean_squared_error(y_true,y_pred)) # 平均绝对误差(MAE) mean_absolute_error(y_true, y_pred)
2> 公式

【标准差】是用来衡量一组数自身的离散程度,
【均方根误差】是用来衡量观测值同真值之间的偏差,它们的研究对象和研究目的不同,虽然计算过程有些相似
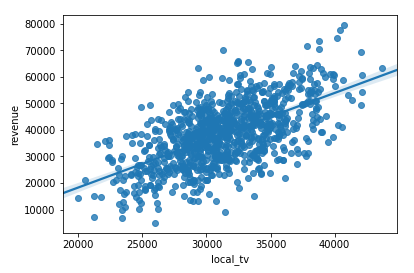
3> 可视化 API
import seaborn as sns sns.regplot('local_tv', 'revenue', df)