一、集中趋势和离中趋势
表示集中趋势的指标们:
均值、中位数、众数、百分位数
异常值判定:
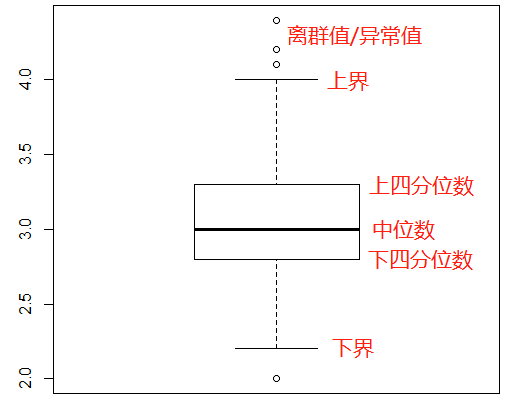
3σ原则原则(还有很多别的原则):超出(μ-3σ,μ+3σ)的值,即超出箱线图上下边界的点
离散程度指标:
极差(range)
标准差(sta.dev)
方差(variance)
变异系数(CV):对标准差做去量纲化,消除两组数据间测量尺度和量纲的影响
通过箱线图来查看集中趋势 (通过R自带的鸢尾花数据集 iris)
iris boxplot(iris[,2])
二、相关系数(cor)
Pearson相关系数
衡量两个数据集合是否在一条线上面,它用来衡量定距变量间的线性关系
Spearman相关系数
衡量排序(秩)一致性
Kendall相关系数
计算多个等级变量相关程度的一种相关量
# 工作时间和薪水 jobtime = c(14,12,11,12,11) salary = c(20000,17000,1650,1670,540) # cor 默认的 method 为 pearson cor(jobtime,salary) # 指定使用 spearman cor(jobtime,salary, method="spearman")
相比于线性关系,案例中的时间与薪水的排序效果更明显,所以此处求得的 Spearman 比 Pearson 更大

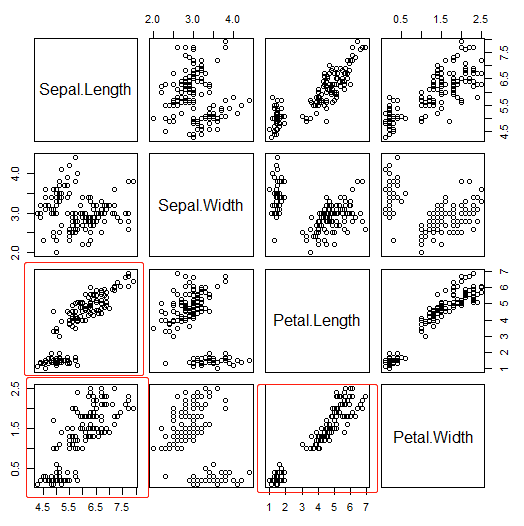
通过两两变量的组合图来查看相关关系(以iris数据集为例)
pairs(iris[,1:4])
通过图,就薛微可以看出来点线性关系
三、描述性统计
summary 函数:查看极值、上下四分位数、均值、中位数
summary(iris[,1:4])
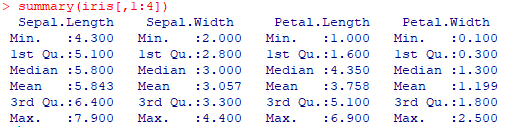
fivenum:返回 极小值, 下四分位数,中位数,上四分位数,极大值
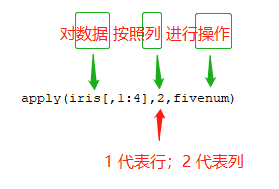
# 求单独一列的fivenum fivenum(iris[,1]) # 求多列的fivenum,借助apply函数 apply(iris[,1:4],2,fivenum)

quantile:返回某分位数处的值
# 求单独一列的分位数
quantile(iris[,1], 0.3)
# 求多列的某分位数的值,借助apply函数
apply(iris[,1:4],2, function(x){return(quantile(x, 0.3))})

Tip:解释一下 apply 函数
四、假设检验
原理:小概率事件实际基本不可能发生
分类:参数检验、非参数检验
H0 原假设:想证明它是错的
H1 备择假设:希望它是对的
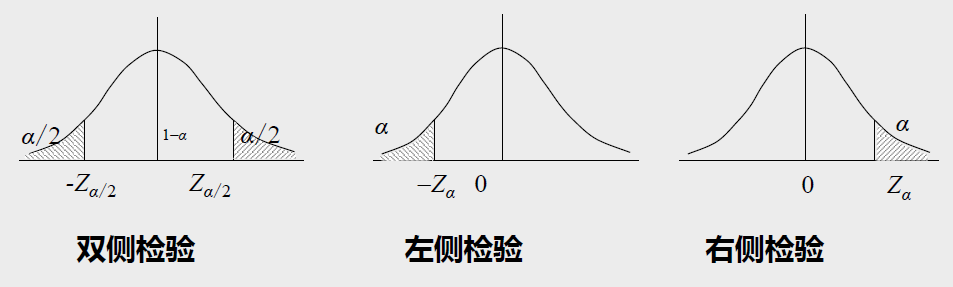
H1与“不相等”对应的是双侧检验,与“小于”相对应的是左侧检验,与“大于”相对应的是右侧检验。(显然hhhhhh)
案例:
单样本 t 检验
t.test(iris[,1])
双样本 t 检验
# 选取两个要做检验的对象 setosa_Sepal_Length = iris[which(iris$Species=="setosa"), "Sepal.Length"] versicolor_Sepal_Length = iris[which(iris$Species=="versicolor"), "Sepal.Length"] # 双样本 t 检验 t.test(setosa_Sepal_Length,versicolor_Sepal_Length)

别的写了再补充