统计知识 | 决定系数 R方、调整后的R方、F值

指标的意义：

• R方：拟合出来的线能解释多少实际信息量
• F值：验证模型整体显著性水平

一、R²

　　也称 拟合优度、决定系数：反应回归模型拟合数据的优良程度

　　先说结论：R² 越接近 1 ，拟合效果越好

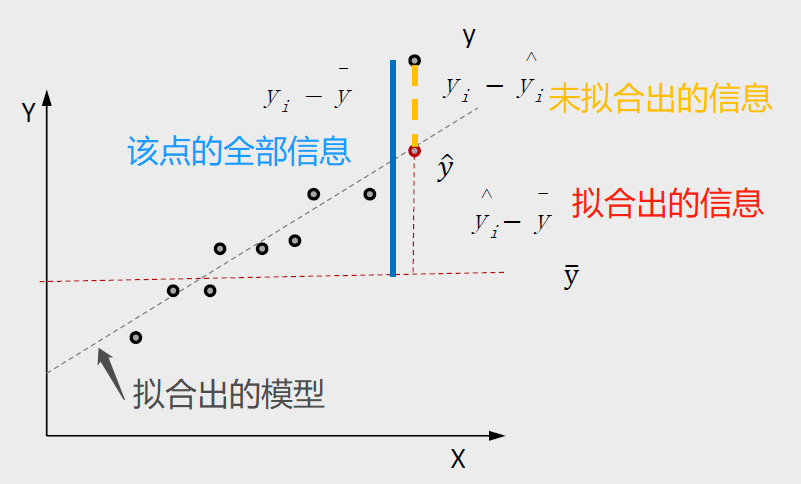
• 回归：所有实际数值点向均值回归，认为均值含有所有点最大的信息量
• 实际信息：点的实际值 减去 均值 认为是 这个点的实际信息（蓝色条），可以拆分成下面两部分
• 误差信息：实际值减线上的点的值，这是未拟合出来的信息（黄色条）
• 拟合出的信息：拟合出来的线上的点 减 均值 （红色条）

对于一个模型来说：误差信息越短，拟合出的信息越长，拟合效果越好。

拟合优度涉及的三个指标

 

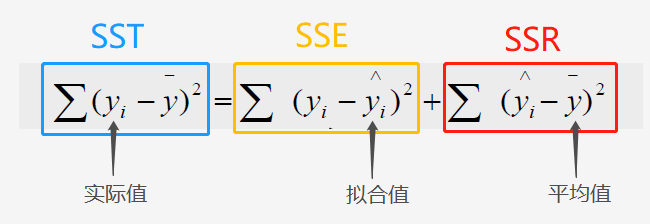
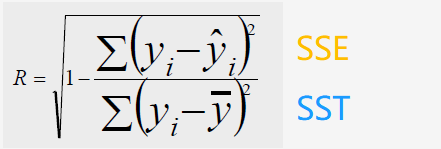
1. SST：总体平方和，它的大小描述了数据集中的数的分散程度

2. SSE：残差平方和 

3. SSR：回归平方和，拟合数据的分散情况

二、调整后的 R²

在样本容量一定的情况下，增加解释变量必定使得自由度减少

目的：在模型的复杂程度和衡量模型的优良程度上取一个平衡

　　让模型趋于简单（模型复杂之后 会使预测受到一定限制：过拟合）

　　所以注意！多元统计要用调整后的R²来衡量

具体操作：将残差平方和与总离差平方和分别除以各自的自由度，以剔除变量个数对拟合优度的影响

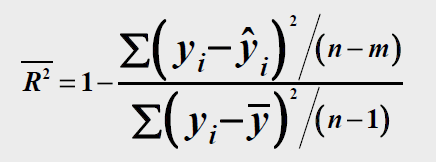
三、F 值

　　先说结论：F 值越大，模型整体显著性水平越高

　　意义：所估计回归的总显著性的一个度量，也是调整后的R方的一个显著性检验

　　即：验证模型整体显著性水平的指标：F值越大越拒绝 0 假设

检验模型中的参数 β 们是否显著不为 0 

 

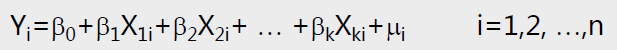
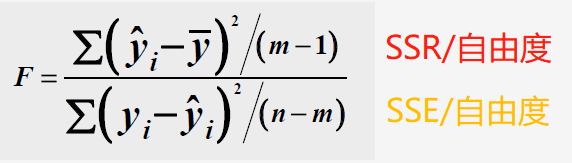
　　由于 SSR 是解释变量 X 的联合体对被解释变量 Y 的线性作用的结果，考虑SSR/SSE的比值：

　　　　如果这个比值较大，可认为总体存在线性关系；

　　　　反之总体上可能不存在线性关系。

　　F值与调整后的R方呈同向变化

　　　　当调整后的R方为 0 时，F = 0；

　　　　调整后的R方越大，F值越大；

　　　　当调整后的R方 为1 时，F值 为正无穷。