一、问题描述
解决最短路径问题。
- 对于内网图而言(边带权值),最短路径是指两顶点之间经过的边上权值之和最小的路径。
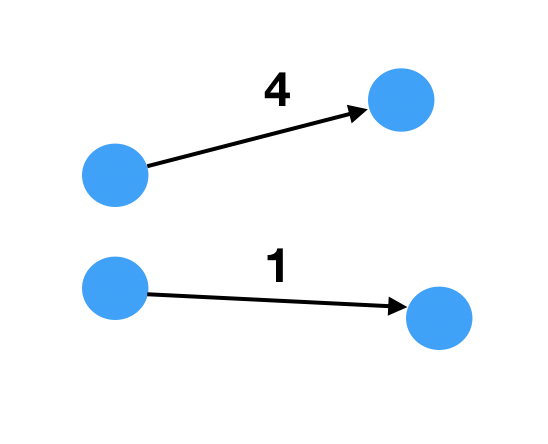
- 对于非内网图而言(边不带权值),最短路径就是经过的边数和最小的路径。
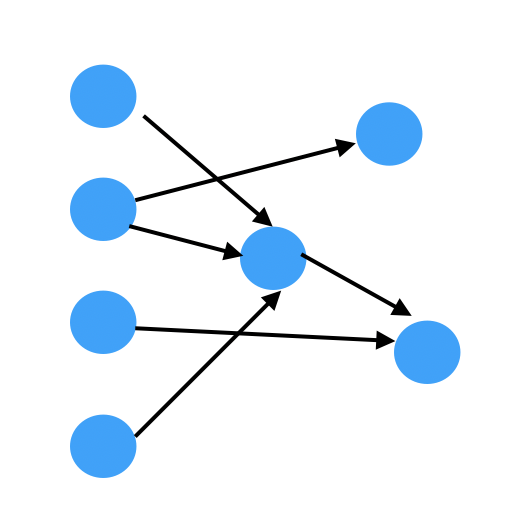
路径中,第一个顶点为源点,最后一个顶点为终点。所求得是源点到终点的最短路径。
二、Dijkstra算法思想
图可以表示为,G(V, E),V为各个顶点,E为各个顶点所连的边,W为各个边的权值。
记顶点为V0,目标点为Vj,Vk为V0到Vj中间任意一点。
- 每次遍历开始都可以确定目前与V0连接的最短路径
- 与V0直连的点未必就是最短路径,除非与V0直连的点距离最短,可以简单证明。
- 若与V0直连的点Vi不是最短路径,那么其只可能被最短路径更新成更短的路径。D(Vi) = Min(D(Vi), D(VK) + W(VK, Vi)),其中VK为目前的最短路径的顶点。
- 最短路径已经是不可能再变的了,因为其它路径都比它长,所以不可能以其它路径当成中间点。
因此思想就可以总结出来了:每次都选择最短路径的顶点为中间点,去更新其它顶点上的权值。贪心思想。
三、Code
1 package algorithm; 2 3 4 /** 5 * Created by adrian.wu on 2019/2/12. 6 */ 7 public class Dijkstra { 8 public int dijkstra(int[][] w, int v0, int vj) { 9 int n = w.length, M = 0x7fffffff; 10 //v0是源点,vj是顶点 11 boolean[] visited = new boolean[n]; 12 int[] D = new int[n]; 13 for (int i = 0; i < n; i++) 14 D[i] = w[v0][i]; 15 16 for (int i = 0; i < n; i++) { 17 int min = M, k = 0; 18 19 for (int j = 0; j < n; j++) { 20 if (min > D[j]) { 21 min = D[j]; 22 k = j; 23 } 24 } 25 26 for (int j = 0; j < n; j++) 27 D[j] = Math.min(D[j], min + w[k][j]); 28 } 29 30 return D[vj]; 31 } 32 }