作为后台服务,通常有一个处理极限PPS(packets per second),如果请求超过了这个处理能力,可能会出现“雪崩效应”,因此后台服务需要有过载保护机制。
1、有个简单的算法可以实现流量控制功能:设置一个单位时间(如1s, 1min)内的最大访问量,并维护一个单位时间里的计数器。
当访问请求到达时,先判断单位控制时间是否已经超时,如果已经超时,重置计数器为0;
否则,将计数器加1,并判断计数器的值是否超过最大访问量设置,如超过,则拒绝访问。
伪代码如下:
1 long timeStamp=getNowTime(); 2 int reqCount=0; 3 const int maxReqCount=10000;//时间周期内最大请求数 4 const long effectiveDuration=10;//时间控制周期 5 6 bool grant() 7 { 8 long now=getNowTime(); 9 if (now <timeStamp+effectiveDuration) 10 { 11 //在时间控制范围内 12 reqCount++; 13 return reqCount>maxReqCount;//当前时间范围内超过最大请求控制数 14 } 15 else 16 { 17 timeStamp=now;//超时后重置 18 reqCount=0; 19 return true; 20 }
21 }
该算法实现确实是实现了“单位时间里最大访问量控制”这一需求,但是,仔细研究下,发现它在两个单位时间的临界值上的处理是有缺陷的。
如:设需要控制的最大请求数为1w, 在第一个单位时间的最后一秒里达到的请求数为1w,接下来第二个单位时间内的第一秒里达到请求数也是1w,由于超时重置发生在两个单位时间之间,
所以这2w个请求都将通过控制,也就是说在2s里处理2w个请求,与我们设置的10s里1w个请求的需求相违背。
2 漏桶算法
漏桶算法思路很简单,请求先进入到漏桶里,漏桶以固定的速度出水,也就是处理请求,当水加的过快,则会直接溢出,也就是拒绝请求,可以看出漏桶算法能强行限制数据的传输速率。
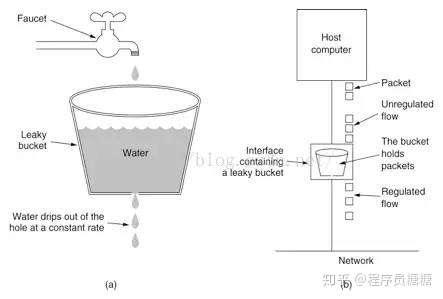
漏桶算法:
1 long timeStamp = getNowTime(); 2 int capacity = 10000;// 桶的容量 3 int rate = 1;//水漏出的速度 4 int water = 100;//当前水量 5 6 public static bool control() { 7 //先执行漏水,因为rate是固定的,所以可以认为“时间间隔*rate”即为漏出的水量 8 long now = getNowTime(); 9 water = Math.max(0, water - (now - timeStamp) * rate); 10 timeStamp = now; 11 12 if (water < capacity) { // 水还未满,加水 13 water ++; 14 return true; 15 } else { 16 return false;//水满,拒绝加水 17 } 18 }
(这里漏桶算法只实现了一半,只是进入流量的处理方式,桶没满,就进桶,满了就拒绝。流量出的逻辑是写入FIFO队列,再按照均匀的速度落到后端)
该算法很好的解决了时间边界处理不够平滑的问题,因为在每次请求进桶前都将执行“漏水”的操作,再无边界问题。
漏桶:用于控制网络中的速率。在该算法中,输入速率可以变化,但输出速率保持恒定。
常常配合一个FIFO队列使用,调用上述control接口,返回true时放入队列,返回false则直接丢弃。
同时使用一个定时器,以恒定的速率从FIFO中消费请求。
3、令牌桶算法
令牌桶算法的原理是系统会以一个恒定的速度往桶里放入令牌,而如果请求需要被处理,则需要先从桶里获取一个令牌,当桶里没有令牌可取时,则拒绝服务。从原理上看,令牌桶算法和漏桶算法是相反的,一个“进水”,一个是“漏水”。
1 long timeStamp=getNowTime(); 2 int capacity; // 桶的容量 3 int rate ; //令牌放入速度 4 int tokens; //当前水量 5 6 bool grant() { 7 //先执行添加令牌的操作 8 long now = getNowTime(); 9 tokens = min(capacity, tokens+ (now - timeStamp)*rate); 10 //令牌已用完,拒绝访问 11 if(tokens < 1) { 12 return false; 13 } else { 14 //还有令牌,领取令牌 15 timeStamp = now; 16 tokens--; 17 retun true; 18 } 19 }
