数值分析实验之矩阵的LU分解及在解线性方程组中的应用（MATLAB 代码）

详细实验指导见上一篇，此处只写内容啦

求如下4阶矩阵的LU分解。

        

• LU分解法

函数定义：
function x=solvebyLU(A,b)% 该函数利用LU分解法求线性方程组Ax=b的解
flag=[exist('A'),exist('b')];
if flag==0
disp('该方程组无解！');
x=[];
return;
else
r=rank(A);
[m,n]=size(A);
[L,U,P]=lu(A);
b=P*b;% 解Ly=b
y(1)=b(1);
if m>1
for i=2:m
y(i)=b(i)-L(i,1:i-1)*y(1:i-1)';
end
end
y=y';% 解Ux=y得原方程组的一个特解
x0(r)=y(r)/U(r,r);
if r>1
for i=r-1:-1:1
x0(i)=(y(i)-U(i,i+1:r)*x0(i+1:r)')/U(i,i);
end
end
x0=x0';
if flag==1  %若方程组有唯一解
x=x0;
return;
else %若方程组有无穷多解
format rat;
Z=null(A,'r'); %求出对应齐次方程组的基础解系
[mZ,nZ]=size(Z);
x0(r+1:n)=0;
for i=1:nZ
t=sym(char([107 48+i]));
k(i)=t; %取k=[k1,k2...,];
end
x=x0;
for i=1:nZ
x=x+k(i)*Z(:,i); %将方程组的通解表示为特解加对应齐次通解形式
end
end
end

命令行窗口输入：
A=[10 7 8 7;7 5 6 5;8 6 10 9;7 5 9 10];
b=[32 23 33 31]';
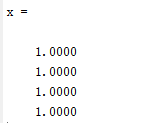
x=solvebyLU(A,b)
[L,U,P]=lu(A)

　运行结果：

        

       

• 不选主元素的三角分解法

%%不选主元素的三角分解法
A=[10,7,8,7;7,5,6,5;8,6,10,9;7,5,9,10];
%A=[6,2,1,-1;2,4,1,0;1,1,4,-1;-1,0,-1,3];
b=[32;23;33;31];
[m,n]=size(A);
L=zeros(m,n);
U=zeros(m,n);
y=zeros(m,1);
x=zeros(m,1);
for i=1:m
    U(1,i)=A(1,i);
    L(i,1)=A(i,1)/U(1,1);
end
for k=1:m-1
    for j=k+1:m
        U(k+1,j)=A(k+1,j);
        L(j,k+1)=A(j,k+1)/U(k+1,k+1);
        for r=1:k
        U(k+1,j)=U(k+1,j)-L(k+1,r)*U(r,j);
        L(j,k+1)=L(j,k+1)-L(j,r)*U(r,k+1)/U(k+1,k+1);
        end
    end
    L(k+1,k+1)=1;
end
y(1,1)=b(1,1);
for i=2:m
     y(i,1)=b(i,1);
    for r=1:i-1
    y(i,1)=y(i,1)-L(i,r)*y(r,1);
    end
end
x(m,1)=y(m,1)/U(m,m);
for i=m-1:-1:1
    x(i,1)=y(i,1)/U(i,i);
    for r=i+1:m
        x(i,1)=x(i,1)-U(i,r)*x(r,1)/U(i,i);
    end
end

　运行结果：