社交网络算法
1、应用场景
在社交网络中社区圈子的识别
基于好友关系为用户推荐商品或内容
社交网络中人物影响力的计算
信息在社交网络上的传播模型
虚假信息和机器人账号的识别
基于社交网络信息对股市的预测
互联网金融行业中的反欺诈模型
2、社交网络算法的分析指标
1)度(Degree)
连接点活跃性的度量;与点相连的边的数目。在有向图中,以顶点A为起点记为出度(out degree)OD(A),以顶点A为终点入度(In degree)ID(A),则顶点A的度为D(A) = OD(A) + ID(A)。
计算方法:
g = Graph([(0,1), (0,2), (2,3), (3,4), (4,2), (2,5), (5,0), (6,3), (5,6)])
g.degree()
ecount = g.ecount()#统计边的数目
vcount = g.vcount()#统计节点数目
maxdegree = g.maxdegree()#最大度值
2)紧密中心性(closness centrality)
节点V到达其他节点的难易程度,也就是到其他所有节点距离的平均值的倒数。
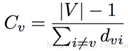
实现方法:
ccvs = []
for p in zip(g.vs, g.closeness()):
ccvs.append({"name": p[0], ["name"], "cc": p[1]})
sorted(ccvs, key=lambda k: k['cc'], reverse=True)[:10]
3)介数中心性
如果一个成员A位于其他成员的多条最短路径上,那么成员A的作用就比较大,也具有较大的介数中心性。
本质:网络中包含成员B的所有最短路径条数占所有最短路径条数的百分比。
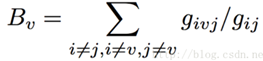
计算步骤:
1.计算每对节点(i,j)的最短路径(需要得到具体的路径)
2. 对各节点判断v是否在最短路径下
3. 累加经过v的最短路径条数
btvs = []
for p in zip(g.vs, g.betweenness()):
btvs.append({"name": p[0]["name"], "bt": p[1]})
sorted(btvs, key=lambda k: k['bt'], reverse=True)[:10]
3、社区发现算法
3.1 GN 算法
边介数(betweenness):
网络中经过该边的最短路径占所有最短路径的比例。
GN算法计算步骤:
1. 计算网络中所有边的介数
2. 找到介数最高的边,并将它从网络中移除
3. 重复以上步骤,直到每个节点就是一个社区为止。

3.2 Louvain 算法
Louvain算法是基于模块度的算法,其优化目标就是最大化整个社区网络结构的模块度。
模块度
它的物理含义是社区内节点的连边数与随机情况下节点的连边数之差,它可以衡量一个社区紧密程度的度量。因此模块度就可以作为优化函数优化社区的分类。
计算方法如下:

其中,Aij节点i和节点j之间边的权重,网络不是带权图时,所有边的权重可以看做是1;ki=∑jAij表示所有与节点i相连的边的权重之和(度数);ci表示节点i所属的社区;m=∑ijAij表示所有边的权重之和(边的数目), 取值范围:[-1/2, 1)。
公式中Aij−=Aij−ki,节点j连接到任意一个节点的概率是现在节点i有ki的度数,因此在随机情况下节点i与j的边为.
δ(ci, cj)将所有的节点都限制在一个社区中,另一个重点是ki和kj都是包括与其他社区相连的边数,因此是在随机情况下节点i和节点j的边数。
基于模块度的社区发现算法,都是以最大化模块度Q为目标。
算法思想
Louvain算法的思想很简单:
1)将图中的每个节点看成一个独立的社区,次数社区的数目与节点个数相同;
2)对每个节点i,依次尝试把节点i分配到其每个邻居节点所在的社区,计算分配前与分配后的模块度变化Delta Q,并记录Delta Q最大的那个邻居节点,如果maxDelta Q>0,则把节点i分配Delta Q最大的那个邻居节点所在的社区,否则保持不变;
3)重复2),直到所有节点的所属社区不再变化;
4)对图进行压缩,将所有在同一个社区的节点压缩成一个新节点,社区内节点之间的边的权重转化为新节点的环的权重,社区间的边权重转化为新节点间的边权重;
5)重复1)直到整个图的模块度不再发生变化。
使用图来表示算法的过程:
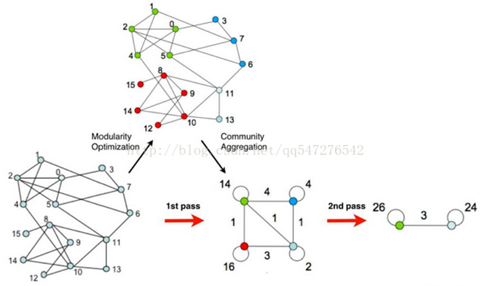
3.3 LPA与SLPA
LPA算法思想:
1. 初始化每个节点,并赋予唯一标签
2. 根据邻居节点最常见的标签更新每个节点的标签
3. 最终收敛后标签一致的节点属于同一社区
SLPA算法思想:
SLPA是LPA的扩展。
1. 给每个节点设置一个list存储历史标签
2. 每个speaker节点带概率选择自己标签列表中标签传播给listener节点。(两个节点互为邻居节点)
3. 节点将最热门的标签更新到标签列表中
4. 使用阀值去除低频标签,产出标签一致的节点为社区。