数据清洗

 

异常值

异常值分析，也叫离群点分析

简单的统计量分析：常见统计量是最大值和最小值，用来判断变量是否超出了合理的范围

3σ原则：如果数据服从正态分布，异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。

箱型图分析：

箱型图提供了识别异常值的一个标准：异常值通常被定义为小于Q_L – 1.5IQR或者大于Q_U + 1.5IQR的值。

Q_L是下四分位数，Q_U是上四分位数，IQR是上下四分位间距。

箱型图绘制代码：

plt.figure() #建立图像

p = data.boxplot(return_type='dict') #画箱线图，直接使用DataFrame的方法

x = p['fliers'][0].get_xdata() # 'flies'即为异常值的标签

y = p['fliers'][0].get_ydata()

y.sort() #从小到大排序，该方法直接改变原对象

#用annotate添加注释

#其中有些相近的点，注解会出现重叠，难以看清，需要一些技巧来控制。

#以下参数都是经过调试的，需要具体问题具体调试。

for i in range(len(x)):

  if i>0:

    plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))

  else:

    plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))

plt.show() #展示箱线图

 

异常值的处理：

1）删除含有异常值的记录

2）视为缺失值

3）平均值修正

4）不处理

不一致的值

举例：号称在他国但ip一直在大陆的新闻阅读者

直接对不一致的的数据进行数据挖掘，可能会产生与实际违背的挖掘的结果

缺失值

确实值的影响：

丢失大量的有用的信息

模型表现出来的不确定性增加

包含空值的数据会使建模过程陷入混乱，导致不可靠的输出

缺失值的处理：

删除存在缺失值的记录

对可能值进行插补

不处理

常用的插补方法：

均值、中位数、众数

使用固定值

最近邻插值：在记录中找到与缺失样本最接近的样本的该属性值插补

回归方法：根据已有数据和与其有关的其他变量（因变量）的数据建立拟合模型来预测缺失的属性值

插值法：拉格朗日插值法、牛顿插值法、Hermite插值、分段插值、样条插值法

拉格朗日插值法：

对于平面上已知的n个点可以找到一个n-1次多项式y = a₀ + a₁x + a₂x² +….+ a_n-1x^n-1，使得多形式曲线过这n个点

然后求出已知的过n个点的n-1次多项式，将缺失的函数值对应的点x代入插值多项式得到缺失值的近似值。

 

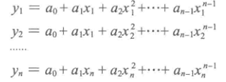
拉格朗日插值公式结构紧凑，在理论分析中很方便，但是当插值节点增减时，插值多项式就会随之变化，这在实际计算中是很不方便的，为了克服这一缺点，提出了牛顿插值法。

from scipy.interpolate import lagrange #导入拉格朗日插值函数     

#自定义列向量插值函数

#s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5

def ployinterp_column(s, n, k=5):

  y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))] #取数

  y = y[y.notnull()] #剔除空值

  return lagrange(y.index, list(y))(n) #插值并返回插值结果

#逐个元素判断是否需要插值

for i in data.columns:

  for j in range(len(data)):

    if (data[i].isnull())[j]: #如果为空即插值。

      data[i][j] = ployinterp_column(data[i], j)

牛顿插值法：

1）求已知的n个点对(x1, y1), (x2, y2)….(xn, yn)的所有阶差商公式

 

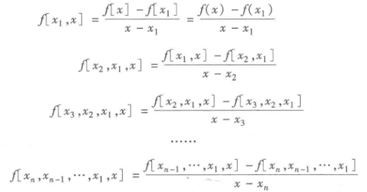
2）联立以上差商公式建立如下插值多项式

 

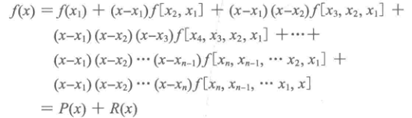
其中：

 

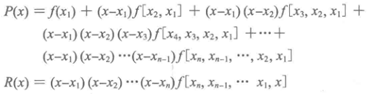
P(x)是牛顿插值逼近函数，R(x)是误差函数

将缺失的函数值对应的点x代入插值多项式得到缺失值的近似值

与拉格朗日插值法相比，具有承袭性和易于变动节点的特点。